Метод потенциалов решения ТЗ

Векторы U = (u ₁, u ₂...., u _m) и V = (v ₁, v ₂...., v _n) называются потенциалами поставщиков и потребителей соответственно, если их координаты удовлетворяют соотношениям u _i + v _j = c _ij, для х _ij > 0, i = 1,2,…, m, j = 1,2,…, п.

Теорема. Если для всех базисных клеток решения (x _ij > 0) u _i + v _j = c _ij, а для всех свободных клеток (x _ij = 0) u _i + v _j ≤ c _ij ,, то решение x _ij является оптимальным и никакими способами улучшено быть не может.

Если среди свободных клеток найдется хотя бы одна, в которой величина ∆_ij = u _i + v _j - c _ij > 0 при x _ij =0, то решение может быть улучшено. Процесс улучшения решения состоит в определении вводимой и выводимой клеток транспортной таблицы. В таблицу вводится клетка, для которой ∆_ij максимальна. Выводимая клетка определяется с помощью цикла.

 

Правило построения цикла:

В соответствии со свойствами ТЗ для невырожденного базисного решения в таблице можно образовать замкнутую цепочку, состоящую только их вертикальных и горизонтальных звеньев, одной из вершин которой является выбранная свободная клетка, а остальные – занятые клетки. Логика построения цикла проста: «выйдя» из свободной, вводимой в базис, клетки в горизонтальном направлении, мы должны «остановиться» в той занятой клетке таблицы, из которой сможем двигаться дальше по вертикали до следующей занятой клетки. В вертикальном направлении переходим к следующей такой занятой клетке, чтобы, повернув в ней в горизонтальном направлении, мы смогли перейти к следующей занятой клетке, и далее аналогично выстраиваем цепочку таким образом, чтобы вернуться к исходной клетке и образовать замкнутый цикл.

Переход от одного опорного решения ТЗ к другому производится с помощью цикла. В построенном цикле, начиная с вводимой клетки (которая считается первой), помечаются вершины:

нечетные знаком «+»,

а четные знаком «–».

Среди множества клеток, помеченных знаком «–», выбирается клетка с наименьшим значением x _ij (обозначим его Q). Затем производится пересчет плана по цепочке: к объемам перевозок в клетках, помеченных знаком «+», добавляется объем Q, а из клеток, помеченных знаком «–», этот объем вычитается. В результате в базис решения вводится исходная клетка цикла с объемом Q и выводится клетка цикла, объем которой был равен Q. Если новое базисное решение не оптимально, то описанная процедура продолжается до получения оптимального решения.

Алгоритм решения ТЗ методом потенциалов.

1. Проверить уравнение баланса (2.4). При необходимости выровнять баланс введением фиктивного поставщика или фиктивного потребителя.

2. Построить начальное опорное решение, например, методом («северо-западного угла» и проверить правильность его составления по количеству базисных клеток (их должно быть N = m+ n – 1, остальные клетки – свободные)).

3. Определить потенциалы U = (u ₁, u ₂...., u _m) и V = (v ₁, v ₂,..., _n) по базисным клеткам. Для этого решают систему уравнений

u _i + v _j = c _ij,для х _ij > 0, i = 1,2,…, m, j = 1,2,…, п,

которая имеет бесконечное множество решений. Для нахождения частного решения системы одно из значений потенциала задают произвольно, например, полагают u ₁ = 0.

4. Проверить выполнение условия оптимальности для всех свободных клеток. Для этого вычисляют ∆_ij = u _i + v _j - c _ij > 0 при x _ij = 0.

Если все ∆_ij ≤ 0, то план оптимален, вычисляют значение целевой функции и решение задачи заканчивается.

5. Если хотя бы в одной свободной клетке ∆_ij >0, приступают к улучшению решения путем пе­реброски перевозок по циклу.

6. После этого заново подсчитываются потенциалы и ∆_ij, и, если план все еще не оптимален, процедура улучшения продолжается до тех пор, пока не будет найдено оптимальное решение.

Если в ТЗ получается вырожденное решение, когда число ненулевых клеток меньше чем (т + п- 1), то вырожденность устраняется следующим методом: вырожденное решение дополняется необходимым количеством нулевых клеток (базисных нулей) таким образом, чтобы они позволяли построить цикл и рассчитать полную систему потенциалов, и далее действуют в соответствии с правилами описанного выше алгоритма.

2.2 Задания

Задание 2.2.1

 

Решите транспортную задачу методом потенциалов.

 

Вариант 1 ai bj	Вариант 2 ai bj
Вариант 3 ai bj	Вариант 4 ai bj
Вариант 5 ai bj

 

3. Целочисленное программирование

 

Постановка задачи целочисленного программирования (ЦП)

В общем виде задача ЦП формулируется следующим образом: найти максимум или минимум функции

(3.1)     (3.2)   (3.3) (3.4)

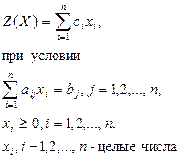
Метод Гомори решения задачи ЦП

( метод отсекающих плоскостей ) основан на следующем подходе: отправной точкой для решения исходной задачи (3.1) - (3.4) является решение задачи (3.1)-(3.3) без учета условий целочисленности (3.4). Если получаемый в результате оптимальный план х* содержит только целые компоненты, то решение задачи ЦП автоматически получено. В противном случае к системе ограничений задачи должно быть добавлено такое ограничение, для которого:

- найденное нецелочисленное оптимальное решение х* не удов­летворяет вновь добавляемому ограничению;

- любое допустимое целочисленное решение задачи (3.1) – (3.4) удовлетворяет вновь добавляемому ограничению.

Такое ограничение называют правильным отсечением. Геометрически правильное отсечение задает гиперплоскость, отсекающую от выпуклого многогранного множества допустимых решенийнекоторого многогранника, не содержащего целочисленных решений.

Правильное отсечение строится следующим образом. Пусть симплекс - методом получено нецелочисленное решение задачи (3.1)-(3.3) без учета условий целочисленности (3.4). Пусть i -е ограничение задачи, находящееся в последней оптимальной симплекс таблице, имеет вид

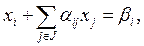
где x _i – базисная переменная в уравнении ограничения;

α_ij – коэффициенты при неизвестных;

x_j – свободные переменные в уравнении ограничения;

β _i – правая часть уравнения (координата оптимального решения), которая является дробным числом;

i – индекс строки с максимальной дробной частью { β _i } числа β _i;

J – множество индексов свободных переменных последней симплекс таблицы.

Тогда дополнительное ограничение (правильное отсечение) имеет вид

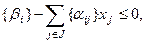(3.5)

где { β _i } – дробная часть β _i;

{ α_ij } - дробная часть α_{ij .}

Напомним, что целой частью [S] числа S называется ближайшее целое, не превосходящее S. Дробная часть {S} числа S есть разность
{S}= S - [S]. Преобразуем неравенство в (3.5) в строгое равенство с помощью введения неотрицательной выравнивающей переменной
x _n+1 ≥ 0, получим

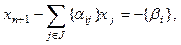(3.6)

Добавив сформированное отсекающее ограничение (3.6) к последней симплекс таблице получаем новую оптимизационную задачу, которую продолжаем решать двойственным симплекс-методом. Для решения задачи ЦП удобно применять модификацию двойственного симплекс-метода, которая совпадает со стандартным алгоритмом симплекс-метода из раздела 1.1 за исключением правила выбора разрешающего элемента. Разрешающий элемент выбирается следующим образом:

- разрешающая строка i берется либо введенная строка отсекающего ограничения (3.6) с целью вывода искусственной переменной x _n+1 из базиса, либо строка с отрицательным свободным членом β _i, в которой есть хотя бы один отрицательный элемент α_ij;

- разрешающий столбец j находим как

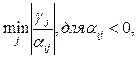
т.е. как минимальное отношение модуля элементов γ _j строки целевой функции Z к отрицательным элементам α_ij.

Если в результате решения двойственным симплекс - методом получаем целочисленное решение, то вычисления заканчиваются, в противном случае составляем новое отсекающее ограничение и процесс решения повторяется.

Доказано, что метод Гомори позволяет получить решение задачи ЦП за конечное число шагов.

Задача не имеет целочисленного решения, если оптимальное решение содержит координату с дробной частью и все коэффициенты соответствующего уравнения являются целыми.

4. Динамическое программирование

 

4.1 Основные определения и понятия

Постановка задачи динамического программирования (ДП)

Пусть экономическая система S может находиться в конечном числе состоянии S_k, k=1,2,… n и является управляемой. Cостояние системы S на k -ом шаге определяется совокупностью чисел x ^(k) = (x ₁^(k),..., х _m^(k)), которые получены в результате реализации управления u _k, обеспечивающего переход системы S из состояния х ^(k-1) в состояние x ^(k).

Будем предполагать, что:

1. состояние x ^(k), в которое перешла система S, зависит от данного состояния х ^(k-1) и выбранного управления u _k и не зависит от того, каким образом система S перешла в состояние х ^(k-1);

2. если в результате реализации k -ro шага обеспечен доход
W _k(x ^(k-1); u _k), зависящий от исходного состояния системы х ^(k-1) и выбранного управления u _k, то общий доход за n шагов cоставляет

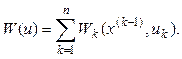
Первое условие называют условием отсутствия последействия, а второе – условием аддитивности целевой функции задачи.

Задача ДП состоит в нахождении оптимальной стратегии уп­равления, т.е. такой совокупности управлений u * = (u ₁*,..., u _n*), в результате реализации которых система S за n шагов переходит из начального состояния x ⁽°⁾ в конечное x ⁽ⁿ⁾ и при этом общий доход W (u) принимает наибольшее значение.

Принцип оптимальности Беллмана. Каково бы ни было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы доход на данном шаге плюс оптимальный доход на всех последующих шагах был максимальный.

Математическая формулировка принципа оптимальности.

Введем некоторые дополнительные обозначения. Обозначим через F₀(x ^(o)) максимальный доход, получаемый за n шагов при переходе системы S из начального состояния х ^(о) в конечное состояние х ⁽ⁿ⁾ при реализации оптимальной стратегии управления u * = (u ₁*,..., u _n*), а через F_k(x ^(k)) – максимальный доход, получаемый при переходе из любого состояния x ^(k) в конечное состояние х ⁽ⁿ⁾ при оптимальной стратегии управления на оставшихся (n -k) шагах. Тогда

F₀(x ⁽°⁾) = mах [ W ₁(x ⁽°⁾, u ₁)+... + W _n(x ⁽ⁿ⁾, u _n)], (4.1)

u =(u ₁, …, u _n)

F_k(x^(k)) = max [ W _k+1(x ^(k), u _k+1)+ F_k+1 (x ^(k+1))] (4.2)

u _k+1

при k = 0,1, …, n -1.

Выражение (4.2) представляет собой математическую запись принципа оптимальности Беллмана и носит название основного функционального уравнения Беллмана. Используя уравнение (4.2) находится решение рассматриваемой задачи динамического программирования.

Алгоритм решения задач динамического программирования

Из принципа оптимальности следует, что оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на n -м шаге, затем на двух последних шагах, затем на трёх последних шагах и т.д., вплоть до первого шага. Таким образом, решение задачи ДП целесообразно начинать с определения оптимального решения на последнем, n -м шаге. Чтобы найти это решение, очевидно, нужно сделать различные предположения о том, как мог окончиться предпоследний шаг, и с учетом этого выбрать управление u _n, обеспечивающее максимальное значение функции дохода W _n(x ^(n-1); u _n). Такое управление, выбранное при определенных предположениях о том, как окончился предыдущий шаг, называется условно оптимальным управлением. Следовательно, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предшествующего шага.

 

Рассмотрим этот процесс более подробно.

Полагая k = n - 1 в уравнении Беллмана (4.2), получим следующее функциональное уравнение:

 

F_n-1(x ^(n-1)) = max [ W _n(x ^(n-1), u _n )+ F_n (x ⁽ⁿ⁾ )] (4.3)

u _n

В уравнении (4.3) F_n (x ⁽ⁿ⁾) можно считать известным. Ис­пользуя теперь уравнение (4.3) и рассматривая всевозможные допустимые состояния системы S на (n -1)-ом шаге x ₁^(n-1), x ₂^(n-1),..., х _i^(n-1),... находим условные оптимальные решения

 

u _n (x ₁^(n-1) ), u _n (x ₂^(n-1)),..., u _n (x _i^(n-1) ), …

 

и соответствующие значения функции (5.3):

 

F_n-1(x ₁^(n-1) ), F_n-1 (x ₂ ^(n-1)),..., F_n-1 (x _i^(n-1))_.

 

Таким образом, на n -ом шаге находим условно оптимальное управление при любом допустимом состоянии системы S после (n -l)-гo шага, т.е. в каком бы состоянии система не оказалась после (n -l)-гo шага, нам уже известно, какое следует принять решение на n -м шаге.

Перейдем теперь к рассмотрению функционального уравнения при k = n -2:

 

F_n-2(x ^(n-2)) = max [ W _n-1(x ^(n-2), u _n-1)+ F_n-1 (x ^(n-1))]. (4.4)

u _n-l

 

Решая функциональное уравнение (4.4) при различных состояниях на (n -2)-ом шаге, получим условно оптимальные управления u _n-1 (х _i^(n-2)), i=1,2,....

Каждое из этих управлений совместно с уже выбранным управлением на последнем шаге обеспечивает максимальное значение дохода на двух последних шагах. Последовательно осуществляя описанный выше итерационный процесс, дойдем, до первого шага. На этом шаге известно, в каком состоянии может находиться система. Поэтому уже не требуется делать предположений о допустимых со­стояниях системы, а остается лишь только выбрать управление, которое является наилучшим с учетом условно оптимальных управлений, уже принятых на всех последующих шагах.

Чтобы найти оптимальную стратегию управления, т.е. определить искомое решение задачи ДП, нужно теперь пройти всю последовательность шагов, только на этот раз от начала к концу. А именно: на первом шаге в качестве оптимального управления u ₁* возьмем найденное условно оптимальное управление u ₁. На втором шаге найдем состояние х ₁*, в которое переводит систему управление u ₁*. Это состояние определяет найденное условно оптимальное управление u ₂^o, которое теперь будем считать оптимальным. Зная u ₂*, находим х ₂^*, а значит, определяем u ₃*и т.д. В результате этого находим решение задачи ДП, т.е. максимально возможный доход и оптимальную стратегию управления, включающую оптимальные управления на отдельных шагах.

 

4.2. Задания

Задание 4.2.1

 

Решить задачу распределения инвестиций методом динамического программирования

 

Задача распределения инвестиций: распределить В единиц средств среди n предприятий, доход g _i(x _j), i=1,2,…, n от которых в зависимости от количества вложенных средств x _i, j =1,2,…, m задается матрицей (n x m +1) (дана в таблицах вариантов задания), таким образом, чтобы суммарный доход со всех предприятий был максимальным. Состояние системы перед каждым шагом определяется числом еще не распределенных средств.

Указание: разбить процесс оптимизации на n шагов так, чтобы на каждом k -м шаге оптимизировать инвестирование не всех предприятий, а только предприятий с k -го по n -ое. При этом считаем, что в остальные предприятия (с первого по (k -1)-ое) тоже вкладываются средства, и поэтому на инвестирование предприятий с k –го по n-ое остаются не все средства, а меньшая сумма c _k ≤ B.

 

Вариант 1 n =3, m =5 x i g 1(x j) g 2(x j) g 3(x j)           2,2   2,8     3,2 5,4   4,1 4,8 6,4   5,2 6,2 6,6   5,9 6,4 6,9	Вариант 2 n =3, m =5 x i g 1(x j) g 2(x j) g 3(x j)           2,4 2,1 2,9   3,1 3,5 5,7   4,2 4,9 6,6   5,4 6,4 6,9   6,1 6,7 7,2
Вариант 3 n =3, m =5 x i g 1(x j) g 2(x j) g 3(x j)             1,8 2,5   2,8 2,9 5,1   3,9 4,5     5,1 5,9 6,3   5,6 6,1 6,6	Вариант 4 n =3, m =5 x i g 1(x j) g 2(x j) g 3(x j)           2,6 2,4 3,2   3,3 3,6 5,8   4,5 5,2 6,9   5,5 6,6 7,1   6,3 6,8 7,3
Вариант 5 n =3, m =5 x i g 1(x j) g 2(x j) g 3(x j)           1,8 1,6 2,4   2,6 2,8 5,1   3,7 4,4 6,1   4,8 5,8 6,3   5,5 6,1 6,5

 

5. Графы

 

5.1 Основные определения и понятия

 

• Граф – пара множеств V и X, таких что G = (V, X).
V – множество вершин, X – множество ребер.

• Петля – ребро вида (v,v).

• Кратные рёбра – одинаковые пары в X.

• Ориентированный граф (орграф D) – граф, для которого пары в X упорядочены. Ребра в орграфе называются дугами и обозначаются
(v_i, v_j).

• Вершина и ребро называются инцидентными, если вершина является для этого ребра концевой точкой.

• Степенью вершины V графа G называется число δ (v) рёбер графа, инцидентных вершине v. Если δ (v) = l, тогда v – висячая вершина, если δ (v) = 0, тогда v – изолированная вершина.

• Полустепенью исхода (захода) вершины v орграфа D называется δ ^- (v) – число дуг, исходящих из v (δ ⁺ (v) – число дуг, заходящих в вершину v).

• Маршрутом для графа G (путем для орграфа D) называется последовательность v₁x₁v₂x₂v₃...x_kv_k+1.

• Цепь – незамкнутый маршрут (путь), в котором все рёбра (дуги) попарно различны.

• Простая цепь – цепь, в которой все вершины попарно различны

• Цикл (контур) – замкнутый маршрут (путь), в котором все рёбра (дуги) попарно различны.

• Простой цикл (контур) – цикл (контур), в котором все вершины попарно различны.

• Деревом графа называется его связный подграф без циклов.

• Покрывающее дерево (остов графа) – дерево, содержащее все вершины графа.

• Длина пути – число рёбер (дуг) в маршруте (пути).

• Путь в графе называется минимальным, если он состоит из минимального количества рёбер.

• Матрица смежности графа: А = [ а_ij ], V = {v₁,...,v_n}, Х= {x₁,..., x_m.}

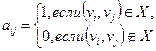
• Матрица инцидентности орграфа D: В = [ b_ij ]

 

 

-8-

• Граф называется нагруженным, если каждой дуге (i, j) поставлено в соответствие число l (i, j), называемое длиной дуги.

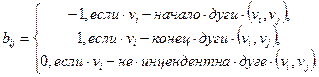
• Матрица длин дуг графа: С = [ с_ij ]

 

 

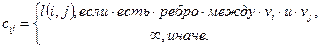
• Путь называется минимальным (кратчайшим) в нагруженном графе или нагруженном орграфе, если он имеет минимальную длину пути.