К пяти признакам, сформулированным ранее, необходимо добавить следующие:
1. в исходной задаче ограничения неравенства следует записывать со знаком ≥, если целевая функция стремится к min, и со знаком ≤, если целевая функция стремится к max;
2. каждому ограничению неравенства исходной задачи соответствует в двойственной задаче условие неотрицательности переменных
u j ≥ 0;
3. каждому условию равенства соответствует переменная u jбез ограничения на знак, и наоборот: неотрицательным переменным xk из основной задачи в двойственной задаче соответствуют ограничения - неравенства, а неограниченным по знаку переменным соответствуют равенства.
Решение двойственных задач опирается на следующие теоремы:
Теорема (первая теорема двойственности).Если одна из пары двойственных задач имеет оптимальное решение, то двойственная к ней задача тоже имеет оптимальное решение. Причем экстремальные значения целевых функций совпадают. Если же одна задача не имеет решения ввиду неограниченности целевой функции, то двойственная ей задача не имеет решения ввиду несовместности системы ограничений.
Теорема (вторая теорема двойственности).Для того чтобы допустимые решения X = (x 1, x 2,..., x n) и U = (u 1, u 2,..., u m) являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие условия сопряжения:

Пара двойственных задач может быть решена симплекс методом. Преобразуем пару двойственных задач к виду, допускающему применение симплекс алгоритма. Для этого введем неотрицательные выравнивающие переменные y j, j = 1,2,…, m в прямую задачу и v i, i = 1,2,…, n – в двойственную задачу:
прямая задача:
 (1.8)
(1.8)
двойственная задача:
 (1.9)
(1.9)
Построим для задач (1.8) и (1.9) общую симплекс-таблицу, причем эта таблица имеет дополнительные столбец и строку для двойственной задачи:
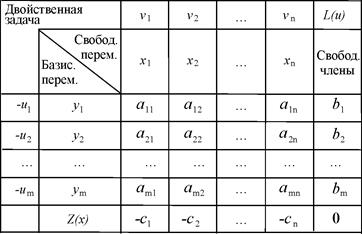
Задачи, представленные в обшей симплекс - таблице, решаются обычным симплекс-методом, алгоритм которого приведен выше. Метод решения с помощью общей симплекс-таблицы называется двойственным симплекс методом.
1.1 Задания
Задание 1.1.1
Составьте математическую модель задачи:
При производстве двух видов продукции используют три вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли.
Вариант 1
| Вид сырья | Норма расхода на 1 изделие | Запас на складе | |
| А | Б | ||
| прибыль от 1 изделия |
Вариант 2
| Вид сырья | Норма расхода на 1 изделие | Запас на складе | |
| А | Б | ||
| прибыль от 1 изделия |
Вариант 3
| Вид сырья | Норма расхода на 1 изделие | Запас на складе | |
| А | Б | ||
| прибыль от 1 изделия |
Вариант 4
| Вид сырья | Норма расхода на 1 изделие | Запас на складе | |
| А | Б | ||
| прибыль от 1 изделия |
Вариант 5
| Вид сырья | Норма расхода на 1 изделие | Запас на складе | |
| А | Б | ||
| прибыль от 1 изделия |
Задание 1.1.2
Составьте математическую модель задачи:
В рационе животных используется два вида кормов. Животные должны получать три вида веществ. Составить рацион кормления, обеспечивающий минимальные затраты.
Вариант 1
| Вид питательного вещества | Содержание питательного вещества в единице корма | Необходимое количество питательного вещества | |
| А | Б | ||
| Стоимость единицы корма |
Вариант 2
| Вид питательного вещества | Содержание питательного вещества в единице корма | Необходимое количество питательного вещества | |
| А | Б | ||
| Стоимость единицы корма |
Вариант 3
| Вид питательного вещества | Содержание питательного вещества в единице корма | Необходимое количество питательного вещества | |
| А | Б | ||
| Стоимость единицы корма |
Вариант 4
| Вид питательного вещества | Содержание питательного вещества в единице корма | Необходимое количество питательного вещества | |
| А | Б | ||
| Стоимость единицы корма |
Вариант 5
| Вид питательного вещества | Содержание питательного вещества в единице корма | Необходимое количество питательного вещества | |
| А | Б | ||
| Стоимость единицы корма |
Задание 1.1.3
Решить ЗЛП графическим методом.
Вариант 1

| Вариант 2
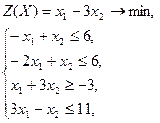
|
Вариант 3

| Вариант 4

|
Вариант 5
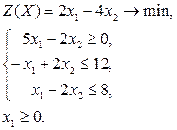
|
Задание 1.1.4
Записать симметричную двойственную пару ЗЛП. Привести к виду для составления общей симплекс - таблицы.
Вариант 1

| Вариант 2

|
Вариант 3

|
Вариант 4

|
Вариант 5

|
2. Транспортная задача
2.1 Основные определения и понятия
Постановка транспортной задачи (ТЗ)
Однородный груз находится у т поставщиков в объемах а 1, а 2...., а m. Груз необходимо доставить n потребителям в объемах b1 , b2,..., bn. Общий объем поставок равен общему объему заявок. Заданы стоимости с ij, i = 1,2,…, m, j = 1,2,…, п доставки единицы груза от каждого поставщика i каждому потребителю j. Требуется рассчитать такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, заявки всех потребителей полностью удовлетворяются и суммарные транспортные издержки минимальны.
Математическая модель ТЗ
|
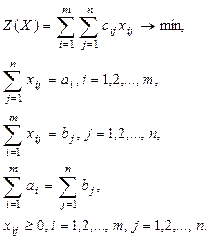
Переменными (неизвестными) ТЗ являются х ij– объемы перевозок от каждого i -го поставщика каждому j -му потребителю. Целевая функция (2.1) выражает требование минимизации транспортных издержек на перевозку всех грузов. Ограничения (2.2) отражают тот факт, что запасы всех m поставщиков вывозятся полностью. Ограничения (2.3) выражает требование полностью удовлетворить заявки всех п потребителей. Ограничения (2.4) называется уравнением баланса и отражает равенство общего объема поставок общему объему заявок.
Математическая формулировка ТЗ: найти такой план перевозок х ij, удовлетворяющий ограничениям (2.2)–(2.5) и обеспечивающий минимум целевой функции (2.1). ТЗ всегда имеет решение, т.к. целевая функция (2.1) ограничена снизу нулем ввиду неотрицательности её слагаемых.
Исходные данные ТЗ записываются в таблице (называемой транспортной таблицей) вида
 b j
a i b j
a i
| b 1 | b 2 | … | b n |
| a 1 | c 11 | c 12 | … | c 1n |
| a 2 | c 21 | c 22 | … | c 2n |
| … | … | … | … | … |
| a m | c m1 | c m2 | … | c mn |
В дальнейшем все действия по нахождению решения ТЗ будут сводиться к преобразованию транспортной таблицы.
Доказано, что система ограничений (2.2)-(2.5) ТЗ имеет ранг
N = m + n – 1, поэтому решение ТЗ не может иметь отличных от нуля координат больше, чем N. Значит, в каждом решении, включая оптимальное, будут отличны от нуля не более, чем (n + т— 1) перевозок х ij. Ячейки (клетки) таблицы, в которых записываются эти отличные от нуля перевозки, называются базисными, а остальные (пустые) - свободными.
Решение ТЗ называется невырожденным, если число ненулевых координат вектора решения X равно N = m + n – 1. Уравнение баланса (2.4) является обязательным условием решения ТЗ.
Когда уравнение баланса нарушено, то в ТЗ необходимо искусственно восстановить баланс следующим способом:
- в ТЗ с избытком заявок вводится фиктивный поставщик с запасом а ф, равным недостающему объему поставок;
- в ТЗ с избытком запасов вводится фиктивный потребитель с заявкой b ф, равной превышающему объему поставок.
Транспортная таблица дополняется в первом случае фиктивной строкой а ф, во втором – фиктивным столбцом b ф. В клетках таблицы, связывающих фиктивные пункты с реальными, стоимости перевозки
с ij = 0.
Метод «северо-западного угла»
Метод «северо-западного угла» построения опорного решения ТЗ: заполнение транспортной таблицы начинается с левой верхней клетки («северо-западного угла») и состоит из однотипных операций. Запасы первого поставщика используются для обеспечения сначала первого потребителя, затем второго и т.д. до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего поставщика и т.д. до полного распределения запасов между потребителями.
После построения начального опорного решения необходимо проверить, чтобы число занятых клеток равнялось N = m + n – 1, т.е. решение было невырожденным.