| Величина коэффициента корреляции | Характер связи |
До 



| Практически отсутствует Слабая Умеренная Сильная |
Значимость линейного коэффициента корреляции проверяется на основе  - критерия Стьюдента:
- критерия Стьюдента:
при 
 ;
;
при 
 .
.
При этом выдвигается и проверяется гипотеза ( ) о равенстве коэффициента корреляции нулю
) о равенстве коэффициента корреляции нулю  . при выполнении
. при выполнении 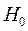
 -статистика имеет распределение Стьюдента с входными параметрами:
-статистика имеет распределение Стьюдента с входными параметрами:  . Если расчетное значение
. Если расчетное значение  (табличное), то гипотеза
(табличное), то гипотеза  отвергается, что свидетельствует значимости линейного коэффициента корреляции, а, следовательно, существенности зависимости между
отвергается, что свидетельствует значимости линейного коэффициента корреляции, а, следовательно, существенности зависимости между  и
и 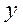 .
.
Таблица 8.3
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |




| Отсутствует Прямая Обратная Функциональная | -
С увеличением  увеличивается увеличивается 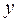 С увеличением
С увеличением  уменьшается уменьшается  Каждому значению факторного признака строго соответствует одно значение результативного признака
Каждому значению факторного признака строго соответствует одно значение результативного признака
|
Коэффициенты ассоциации ( ) и контингенции (
) и контингенции ( ) определяют тесноту связи двух качественных признаков, каждый из которых состоит только из двух групп.
) определяют тесноту связи двух качественных признаков, каждый из которых состоит только из двух групп.
Таблица 8.4
Таблица для вычисления коэффициентов ассоциации и контингенции

| 
| 
|

| 
| 
|
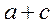
| 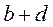
| 
|
 ;
;  .
.
Коэффициент контингенции всегда меньше коэффициента ассоциации; связь считается подтвержденной, если  или
или 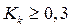 .
.
Коэффициент взаимной сопряженности Пирсона-Чупрова ( и
и  ) определяет тесноту связи более чем двух качественных признаков, каждый из которых состоит более чем из двух групп.
) определяет тесноту связи более чем двух качественных признаков, каждый из которых состоит более чем из двух групп.
 и
и  ,
,
где  - число значений (групп) первого признака;
- число значений (групп) первого признака;
 - число значений (групп) второго признака;
- число значений (групп) второго признака;
 - показатель взаимной сопряженности, причем
- показатель взаимной сопряженности, причем
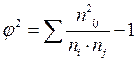 .
.
Таблица 8.5
Вспомогательная таблица для расчета коэффициента
Взаимной сопряженности
 

| I | II | III | Всего |
| I | 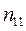
| 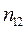
| 
| 
|
| II | 
| 
| 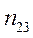
| 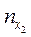
|
| III | 
| 
| 
| 
|
| Итого | 
| 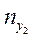
| 
| 
|
Чем ближе величины  и
и  к единице, тем теснее связь качественных признаков.
к единице, тем теснее связь качественных признаков.
Ранг – порядковый номер значения признака, расположенного в порядке возрастания или убывания величин.
Ранжирование – процедура упорядочения объектов изучения, которая выполняется на основе предпочтения значений признака в порядке возрастания или убывания.
Простейшим непараметрическим показателем тесноты связи между признаками  и
и 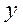 является коэффициент Фехнера (
является коэффициент Фехнера ( ):
):  ,
,
где  - число совпадений знаков отклонений
- число совпадений знаков отклонений  и
и  ;
;
 - число несовпадений знаков отклонений
- число несовпадений знаков отклонений  и
и  .
.
Коэффициент Фехнера  , причем при
, причем при  связь между признаками
связь между признаками  и
и  функциональная, а при
функциональная, а при  связь отсутствует.
связь отсутствует.
Коэффициенты корреляции рангов (коэффициент Спирмена) (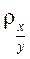 ) определяют тесноту связи между двумя количественными или качественными признаками после предварительного ранжирования их по возрастанию или убыванию.
) определяют тесноту связи между двумя количественными или качественными признаками после предварительного ранжирования их по возрастанию или убыванию.  ,
,
где  - квадрат разности рангов
- квадрат разности рангов  ;
;
 - число наблюдений (число пар рангов).
- число наблюдений (число пар рангов).
Значимость коэффициента корреляции рангов Спирмена проверяется на основе  -критерия Стьюдента. Расчетное значение критерия определяется по формуле:
-критерия Стьюдента. Расчетное значение критерия определяется по формуле:  . Значение коэффициента корреляции считается статистически существенным, если
. Значение коэффициента корреляции считается статистически существенным, если  .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какими статистическими методами исследуются функциональные и корреляционные связи?
2. Какие основные задачи решаются с помощью метода корреляционного и регрессионного анализа?
3. Охарактеризуйте основные правила построения однофакторной линейной регрессионной модели.
4. Что характеризуют коэффициенты регрессии?
5. Зачем необходима проверка адекватности регрессионной модели?
6. Как осуществляется проверка значимости коэффициентов регрессии?
7. Какими показателями измеряется теснота корреляционной связи?
8. Линейные коэффициенты корреляции и детерминации, их смысл и значение.
9. Проверка существенности показателей тесноты связи как необходимое условие распространения выводов по результатам выборки на всю генеральную совокупность. Как она осуществляется?
10. Какой экономический смысл имеет коэффициент эластичности?
11. Сущность и назначение парных и частных коэффициентов корреляции.
12. Сущность и значение совокупного коэффициента множественной корреляции и совокупного коэффициента детерминации.
13. Каким образом выделить факторы, в изменении которых заложены наибольшие возможности в управлении изменением результативного признака?
14. Какие непараметрические методы применяются для моделирования связи?