Определить форму связи – это значит выявить механизм получения зависимой случайной переменной. При изучении математических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т. д.). Регрессия – это односторонняя стохастическая зависимость. Она устанавливает соответствие между случайными переменными. Например, при изучении потребления энергии (y) в зависимости от объема производства (х) речь идет об определении односторонней связи, следовательно, о регрессии.
Односторонняя стохастическая зависимость выражается с помощью функции, которая, для отличия ее от строгой математической функции, называется функцией регрессии или просто регрессией.
Отметим, что функция регрессии не обратима, если за стохастической связью не скрывается функциональная подлинная зависимость.
Для характеристики формы связи при изучении корреляционной зависимости пользуются понятием кривой регрессии. Кривой регрессии h по x
(или h на x) называется условное среднее значение случайной переменной h, рассматриваемой как функции от х, т.е.
.
Функция 
даст наименьшую среднюю погрешность оценки прогноза. Определение корреляционной связи было дано безотносительно к совместному закону распределения переменных (x, h), т.е. корреляционную связь можно исследовать при любом законе распределения (x, h). В дальнейшем мы остановимся на линейной регрессии.
Линейная регрессия или линейная форма связи между случайными переменными занимает особое место в теории корреляции. При такой форме связи есть линейная функция от х:
,
где 
- коэффициенты прямой регрессии; х – независимая переменная.
Коэффициенты регрессии определяются методом наименьших квадратов, т.е. ищется такая прямая линия, сумма квадратов отклонений измеренных значений по результатам опыта уi от которой была бы минимальной
(4.1)
где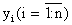 
– значения h по результатам опыта.
Как известно, минимум функции можно найти, приравняв нулю ее первую производную. Запишем (4.1) в виде
,
где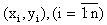 
– наблюдения за (x, h).
Находим частные производные функций Q ( 
, 
) по и и приравниваем их нулю
Сокращая оба уравнения на -2 и производя почленное суммирование, получим
Величины 
являются постоянными и следовательно
(4.2)
Система (4.2) называется системой нормальных уравнений. Разрешив ее относительно и , получим значения коэффициентов регрессии
(4.3)
Воспользуемся тем, что 
, 
следствия из
, 
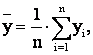
(учтено, что пара чисел (x, y) наблюдалась 
раз).
Обозначим через 
Тогда из (4.3) имеет вид:
Умножим обе части последнего равенства на 
- называется коэффициентом регрессии;
- выборочный коэффициент корреляции.
Тогда выборочное уравнение прямой линии регрессии h на x можно записать в виде
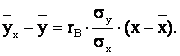
Полученные здесь формулы пригодны для вычислений с помощью ЭВМ или микрокалькулятора, но вычисления “вручную” трудоемки, для их упрощения используется корреляционная таблица.
Замечание 1. Аналогично находят выборочное уравнение прямой линии регрессии x на h
вида:
где 
– коэффициент регрессии.
Замечание 2.
1) 
;
2) Если 
и выборочные линии регрессии – прямые, то x и h не связаны линейной корреляционной зависимостью, возможно они связаны нелинейной или даже функциональной зависимостью;
3) а) Таким образом выборочный коэффициент корреляции характеризует тесноту линейной связи между количественными признаками ввыборке: чем ближе 
к 1, тем связь сильнее и при 
переходит в функциональную зависимость;
б) Знак выборочного коэффициента корреляции совпадает со знаком выборочных коэффициентов регрессии
где 
и 
– соответственно коэффициенты регрeссии.