Образующий полином:
P(x)= x10+x9 +x8 +x6+x5+x3+x2+x+1
Составим порождающую матрицу G состоящую из единичной и проверочной матриц.
 |  | 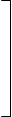 | |||
10000 1111011011
|
00100 0100011011
00010 1101010110

 00001 0110101011
00001 0110101011
Количество разрешенных кодовых комбинаций = 2k =32. Где к=5.
Найдем матрицу проверок Н(15,10) . Она будет состоять из единичной матрицы размерностью 10x10 и матрицы размерности 10x5, которая получается из матрицы 5x10, составленной из проверочных элементов, входящих в матрицу G(15,5) путем ее транспонирования.
 |  |
11010 1000000000
10111 0100000000
10001 0010000000
10010 0001000000
01001 0000100000
Н(15,10)= 11110 0000010000
10101 0000001000
01010 0000000100
11111 0000000010
 10101 0000000001
10101 0000000001
 | |||
 |
Согласно свойству циклического кода dmin равно минимальному числу линейно зависимых столбцов матрицы проверок, т.е. минимальному числу столбцов поразрядная сумма по mod(2) равна нулю.
dmin= 5
Составление таблицы всех разрешенных кодовых комбинаций и определение их веса
Для получения 32 разрешенных кодовых комбинаций необходимо воспользоваться образующей матрицей, где 5 разрешенных комбинаций имеются в явном виде, а остальные разрешенные комбинации получаются при помощи сложения в различных сочетаниях строк этой матрицы.
Таблица всех разрешенных,ненулевых комбинаций
| чв | №к | №строки | Разрешённые кодовые комбинации (КК) | Вес | ||||||||||||||
| И | Н | Ф | О | Р | П | Р | О | В | Е | Р | О | Ч | Н | Ые | ||||

| ||||||||||||||||||
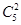
| 1Å2 | |||||||||||||||||
| 1Å3 | ||||||||||||||||||
| 1Å4 | ||||||||||||||||||
| 1Å5 | ||||||||||||||||||
| 2Å3 | ||||||||||||||||||
| 2Å4 | ||||||||||||||||||
| 2Å5 | ||||||||||||||||||
| 3Å4 | ||||||||||||||||||
| 3Å5 | ||||||||||||||||||
| 4Å5 | ||||||||||||||||||
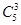
| 1Å2Å3 | |||||||||||||||||
| 1Å2Å4 | ||||||||||||||||||
| 1Å2Å5 | ||||||||||||||||||
| 2Å3Å4 | ||||||||||||||||||
| 2Å3Å5 | ||||||||||||||||||
| 1Å3Å5 | ||||||||||||||||||
| 4Å5Å1 | ||||||||||||||||||
| 4Å5Å2 | ||||||||||||||||||
| 3Å5Å4 | ||||||||||||||||||
| 1Å3Å4 |
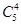
| 1Å2Å3Å4 | |||||||||||||||||
| 1Å2Å3Å5 | ||||||||||||||||||
| 2Å3Å4Å5 | ||||||||||||||||||
| 3Å4Å5Å1 | ||||||||||||||||||
| 1Å4Å5Å2 | ||||||||||||||||||
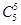
| 1Å2Å3Å4Å5 |
| Кратность ошибки | Число вариантов комбинации ошибок кратности | Число вариантов комбинацийошибок приводящих к НО | Доля НО |
| 0,001 | |||
| 0,001 | |||
| 0,001 | |||
| 0,0008 | |||
| 0,0014 | |||
| 0,0017 | |||
Dmin =5
5>= s + 1 Þ s=4 кратность обнаружения ошибок
5>= 2t +1 Þ t = 2 кратность исправления ошибок
I. Разработка схемы кодирующего устройства
Декодирующее устройство – это регистр сдвига с обратной связью. Количество триггеров регистра равно степени образующего полинома. Число сумматоров в регистре равно количеству знаков + в выражении для образующего полинома. Сумматоры ставятся перед триггерами, соответствующими ненулевым членам образующего полинома.
Таблица состояний регистра сдвига кодера цикличесого кода.
| №такта | G(x) | Т1 | Т2 | Т3 | Т4 | Т5 | Т6 | Т7 | Т8 | Т9 | Т10 | F(x) |
 6 6
| ||||||||||||
Для обнаружения ошибок в принятой кодовой комбинации следует разделить её на образующий полином. Результат деления укажет на наличие или отсутствие ошибки в принятой кодовой комбинации. Если деление дает нулевой остаток, то ошибки отсутствуют или не обнаружены. Если же в результате деления полинома (принятой кодовой комбинации) на образующий полином остаток R’(х) отличен от нуля, то это означает что принятая кодовая комбинация содержит ошибки. Вид ненулевого остатка R’(х), называемого синдромом ошибки.