Реализация фильтров нижних частот

Классификация фильтров

По расположению полосы пропускания фильтры делятся на следующие типы:

-фильтры нижних частот (ФНЧ), пропускающие сигналы с частотами от 0 до ƒ_с;

-фильтры верхних частот (ФВЧ), имеющие полосу пропускания отƒ_с до бесконечности;

-полосовые фильтры (ПФ), пропускающие входной сигнал в полосе частот от f_{c 1} до f_{c 2};

- заграждающие фильтры (ЗФ), не пропускающие входной сигнал в полосе частот от

f_{c 1} до f_{c 2;}

- гребенчатые фильтры (ГФ), или многополосовые, имеющие несколько полос

пропускания.

Аппроксимация характеристик фильтров нижних частот

Функция фильтрации. В общем виде электрические фильтры описываются передаточной функцией вида:
(1)

Квадрат амплитудно-частотной характеристики таких фильтров
(2)
и, следовательно, рабочее ослабление
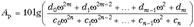(3)
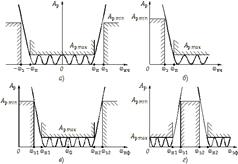
могут при надлежащем выборе степени полинома (порядка фильтра) и коэффициентов d_k удовлетворить заданным требования (см. рис. 3).

В теории фильтров принято иметь дело не с обычной угловой частотой , а с нормированной частотой , где 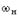– нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания , так что .

В теории электрических фильтров вместо формул (2) и (3) используют другие, также универсальные для любого типа фильтра:
(4)
(5)

Функция 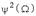называется функцией фильтрации, а – коэффициентом неравномерности ослабления. В общем случае – это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: –1 1 в полосе пропускания и >> 1 в полосе непропускания фильтра.

В зависимости от вида функции фильтрации получают различные типы фильтров. Если в качестве функции фильтрации используют полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров широкое использование нашли фильтры Баттерворта и Чебышева. Если – дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева.

Реализация фильтров нижних частот

Лестничные полиномиальные LС-фильтры. Любые из рас­смотренных выше фильтров, как полиномиальные, так и со всплесками ослабления могут быть реализованы в виде пассив­ных LC-цепей.

Пассивные LC-фильтры обычно представляют собой реактив­ный лестничный четырехполюсник, включенный между генерато­ром с активным внутренним сопротивление R_H п нагрузкой с актив­ным сопротивлением R_Г (рис. 17.10). Входное сопротивление реак­тивного четырехполюсника, нагруженного па сопротивление R_H, обозначено па рисунке Z_BX1(p).

Если фильтр со стороны зажимов 1 — 1' рассматривать как двухполюсник, образованный реактивным четырехполюсником и нагрузкой R_H, то, зная выражение 2_вх1(р), можно реализовать данный двухполюсник одним из известных в теории цепей методов синтеза двухполюсников. Таким образом, задача реализации фильтра сводит­ся к реализации двухполюсника по его заданному входному сопротив­лению. Идея данного подхода принадлежит С. Дарлингтону и метод реализации фильтров называет­ся методом Дарлингтона.

На входе фильтра имеет место несогласованность, которую можно оценить, введя в рассмотрение коэффициент отражения (16.25)

Из (17.27) следует, что знаменатель у σ(р) такой же, как и у Н_р(р): им является полином v(p). Остается найти нули правой час­ти выражения (17.7) и половину из них «приписать» полиному чис­лителя σ (р). Последний формируется из нулей по теореме Виета.

Лестничные фильтры со всплесками ослабления. По подобной схеме осуществляется и реализация передаточных функций фильтров со всплесками ослабления (Чебышева или Золотарева). Разложение входного сопротивления таких фильтров в цепную дробь приведет к схемам, содержащим резонансные контуры, в которых резонансы происходят на частотах ₁, ₂,... Наличие этих контуров и обеспечивает бесконечно большое затухание на частотах всплеска.

Рис. 17.13

Так, ФНЧ пятого порядка со всплесками ослабления на частотах ₁ и ₂ реализуется в виде одной из схем, приведенных на рис. 17.13, а и б. И в первой и во второй схемах контуры рассчитаны на резонансные частоты ₁ и ₂. В первой схеме в параллельных контурах происходят резонансы токов; сопротивления контуров принимают бесконечно большие значения. В результате на частотах резонансов ₁ и ₂ наблюдается "обрыв" продольных ветвей фильтра и сигнал от генератора в нагрузку не поступает, т. е. фильтр вносит бесконечно большое ослабление. Во второй схеме в последовательных контурах происходят резонансы напряжений; сопротивления контуров обращаются в нуль. Таким образом, здесь на частотах ₁ и ₂ поперечные ветви "закорачивают" нагрузку и сигнал на выход фильтра не поступает. Таким образом, имеет место бесконечно большое ослабление.

Реализация лестничных фильтров по каталогам. Из изложенного следует, что синтез фильтров представляет собой сложную процедуру, поэтому разработчики фильтров пытались облегчить ее. В результате были созданы обширные каталоги фильтров, применение которых значительно облегчает процедуру синтеза ФНЧ. Табл. 17.1 представляет собой страницу из такого каталога, где приведены нормированные элементы фильтра Золотарева четвертого порядка. В этой таблице _s, A_s, A_s – нормированная граничная частота полосы задерживания, минимальное ослабление в полосе задерживания, максимальное ослабление в полосе пропускания соответственно. Аналогичные каталоги существуют и для фильтров Баттерворта и Чебышева.