В синтезе электрических цепей часто прибегают к нормированию элементов и частоты. Нормирование частоты уже встречалось ранее, когда рассматривались частотные характеристики колебательных контуров (гл. 4). Целесообразность применения нормирования ясна из следующего примера. Пусть необходимо рассчитать частотную характеристику сопротивления последовательного RLC- контура с параметрами элементов L = 10–5 Гн, С = 10–9 Ф, R = = 5 Ом. Данный контур имеет добротность Q = 20, характеристическое сопротивление 
= 100 Ом и резонансную частоту 
р = 107 с–1. При расчете сопротивления данного контура приходится оперировать с величинами от 10–9 до 107, что не всегда удобно. Выполним нормирование сопротивлений и частоты. Для этого запишем выражение сопротивления данного контура:
Разделим левую и правую часть равенства на некоторое нормирующее значение сопротивления R н, а второе и третье слагаемое умножим и разделим на некоторое нормирующее значение частоты 
н:
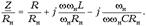
Введем следующие названия и обозначения:
– нормированное комплексное сопротивление,
– нормированная частота
(16.8)
– нормированная индуктивность;
(16.9)
– нормированная емкость;
(16.10)
– нормированное резистивное сопротивление.
Величины н и R н, вообще говоря, можно выбирать произвольно. В данном случае удобно положить н = р и R н = 
. Тогда параметры нормированных элементов принимают следующие значения:
Выполнение расчетов с такими числовыми значениями удобней, чем с ненормированными величинами.
Существует вторая, более важная причина, по которой применяют нормирование. Она проявляется в синтезе цепей. Допустим, что в результате сложных процедур получена некоторая цепь с нормированными значениями элементов. Истинные значения элементов определяются из формул (16.8)—(16.10) следующим образом:
(16.11)
(16.12)
(16.13)
Изменяя 
н и R н можно без выполнения сложных процедур получить схемы устройств, работающих в различных диапазонах частот и при различных нагрузках. Введение нормирования позволило создать каталоги фильтров, что во многих случаях сводит сложную проблему синтеза фильтра к элементарным действиям.
Чувствительность характеристик электрических цепей
Предположим, что каким-то образом синтезирован четырехполюсник. Его характеристики (частотные, или временные) выражаются через его элементы. Например, на рис. 16.2 показана простейшая схема фильтра.
| 
|
| Рис. 16.2 | Рис. 16.3 |
Его операторная передаточная функция имеет вид
(16.14)
Квадрат модуля передаточной функции
Как видно, характеристики цепи зависят от параметров ее элементов. В процессе производства и эксплуатации радиоэлектронных устройств значения параметров элементов неизбежно отличаются от расчетных значений, что приводит к изменению их характеристик. Изменения характеристик должны быть такими, при которых работа устройства не нарушается. Поэтому, чем меньше изменения характеристик при одном и том же отклонении величин параметров элементов, тем лучше это устройство. Для оценки влияния изменений характеристик устройств к изменению параметров элементов вводится понятие чувствительности. Пусть хi i -й элемент (параметр) цепи, а F (хi) – характеристика, зависящая от этого элемента. Чувствительностью некоторой характеристики F (хi) к изменению некоторого параметра хi называется предел отношения относительного изменения функции к относительному изменению параметра:
Например, чувствительность АЧХ цепи | H (j )| к изменению какого-либо параметра цепи xi имеет вид
Кроме чувствительности временных и частотных характеристик в теории цепей рассматриваются также чувствительность полюса и добротности полюса к изменению (параметров) элементов. Для операторной передаточной функции (16.14) полюсы определяются выражением
Здесь предполагается, что полюсы являются комплексно-сопряженными числами. На рис. 16.3 показано положение этих полюсов на комплексной плоскости.
Добротностью полюса называют отношение его модуля (расстояние от полюса до начала координат) к удвоенной вещественной части:
Интересно, что добротность полюса совпадает с добротностью контура на резонансной частоте (см. (4.25)). В предельных случаях, когда полюс находится на мнимой оси, то Q = 
, а когда на вещественной оси – Q = 0,5.
Чувствительность k -го полюса определяется как
где pk – полюс передаточной функции цепи. Эта чувствительность показывает приращение полюса при изменении параметров элементов цепи. В данном случае S – это не функция, а комплексное число.
Чувствительность добротности полюса вычисляется по формуле
Исследование чувствительности при синтезе цепей помогает создать цепь, характеристики которой наименее подвержены воздействию различных дестабилизирующих факторов (например, температуры, влажности, старения элементов и др.).