
1). Какой вид криволинейного движения можно рассматривать как основное?
Ответ. Среди различных видов криволинейного движения особый интерес представляет равномерное движение тела по окружности. Это самый простой вид криволинейного движения. Вместе с тем любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности.
2). Как определяется центростремительное ускорение?
Ответ. При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости v изменяется в процессе движения. Определим ускорение тела, движущегося равномерно по окружности радиусом R. За интервал времени Δt тело проходит путь ΔS = v · Δt. Этот путь ΔS равен длине дуги АВ. Векторы скоростей vA и vB в точках А и В направлены по касательным к окружности в этих точках, угол α между векторами vA и vB равен углу между радиусами ОА и ОВ. Для нахождения вектора ускорения а нужно найти разность векторов скорости Δv = vB — vA и определить отношение изменения скорости к малому интервалу времени Δt, за который произошло это изменение.
Из подобия треугольников ОАВ и BCD следует, что |ОА|/| АВ | = |ВС|/|CD|.
Если интервал времени Δt мал, то мал и угол α. При малых значениях угла α длина хорды АВ
примерно равна длине дуги АВ. Так как |ОА| = R; | АВ | = v · Δt; ВС| = v и |CD| = Δv, то получаем:
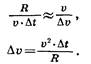
Поскольку
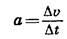 , то
, то 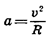
Из рисунка видно, что, чем меньше угол α, тем ближе направление вектора Δv к направлению
на центр окружности. Так как вектор ускорения а равен отношению вектора Δv к интервалу времени Δt при условии, что интервал времени Δt очень мал, то вектор ускорения при равномерном движении по окружности направлен к ее центру.
При изменении положения тела на окружности меняется направление на центр окружности.
Следовательно, при равномерном движении тела по окружности модуль ускорения имеет постоянное значение, но направление вектора ускорения изменяется со временем. Ускорение при равномерном движении по окружности называется центростремительным ускорением.
3). Какие ещё характеристики используют для описания вращательного равномерного движения тела по окружности?
Ответ. Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодом. Период обращения тела по окружности обозначается буквой Т, Т = t/n, где n – число оборотов по окружности, t – время, за которое они совершены. Так как длина окружности S равна 2πR, то период обращения при равномерном движении тела со скоростью v по окружности радиусом R равняется: Т = 2πR/v.
Величина, обратная периоду обращения, называется частотой обращения. Частота обращения обозначается греческой буквой «ню» (ν) и показывает, сколько оборотов по окружности совершает тело в единицу времени: ν = 1/Т, ν = n/t. Единица частоты — 1/с.
4) Какие формулы для вычисления центростремительного ускорения можно получить используя полученные формулы?
Ответ. Используя эти формулы можно получить другие формулы для вычисления центростремительного ускорения:

