Пусть дана функция f (X), ограниченная снизу на множестве  и имеющая непрерывные частные производные во всех его точках.
и имеющая непрерывные частные производные во всех его точках.
Требуется найти безусловный минимум функции f (X) на множестве допустимых решений, то есть найти такую точку  , что
, что
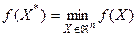 .
.
Стратегия поиска
Разложим функцию f (X) в окрестности точки  в ряд Тейлора:
в ряд Тейлора:
 , (4.2)
, (4.2)
где 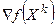 — градиент функции f (X) в точке Xk;
— градиент функции f (X) в точке Xk;  — вектор приращения переменных функции f (X);
— вектор приращения переменных функции f (X);  — члены ряда, имеющие второй порядок и выше.
— члены ряда, имеющие второй порядок и выше.
Ограничимся в выражении (4.2) членами не выше первого порядка, тогда выражение (4.2) примет вид:
 . (4.3)
. (4.3)
Приращение вектора переменных  должно выбираться таким образом, чтобы выполнялось неравенство
должно выбираться таким образом, чтобы выполнялось неравенство  . Уменьшение значения функции в точке
. Уменьшение значения функции в точке  может быть осуществлено за счет выбора 2-го слагаемого, а именно,
может быть осуществлено за счет выбора 2-го слагаемого, а именно,  . В этом случае направление поиска минимума функции будет совпадать с направлением, противоположным градиенту
. В этом случае направление поиска минимума функции будет совпадать с направлением, противоположным градиенту  . Тогда формула (4.1) примет окончательный вид [4,5]:
. Тогда формула (4.1) примет окончательный вид [4,5]:
 . (4.4)
. (4.4)
Замечания
1. Величина шага α вдоль выбранного направления в выражении (4.4) может быть:
- постоянной α =const, и не зависящей от выбора точки Xk и номера итерации; в этом случае реализуется градиентный метод с постоянным шагом;
- может определяться на каждой итерации, и αk вычисляется путем решения задачи минимизации функции f (X) вдоль выбранного направления  на основе методов однопараметрической оптимизации [6]; в этом случае реализуется метод Коши.
на основе методов однопараметрической оптимизации [6]; в этом случае реализуется метод Коши.

Рисунок 6 — Приближение к точке минимума функции на основе метода наискорейшего спуска (Коши).
Алгоритм
Шаг 1. Задать начальную точку X 0, ε 1>0, ε 2>0, предельное число итераций M. Найти градиент функции в произвольной точке.
Шаг 2. Положить k =0.
Шаг 3. Вычислить 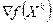
Шаг 4. Проверить выполнение критерия окончания 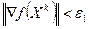 :
:
а) если критерий выполнен, то X *= Xk;
б) иначе перейти к шагу 5.
Шаг 5. Проверить выполнение равенства k ≥ M:
а) если неравенство выполнено, то X *= Xk;
б) иначе перейти к шагу 6.
Шаг 6. Вычислить величину αk в соотношении  на основе метода квадратичной аппроксимации [6], положив αk 1=0, Δ α =0,1.
на основе метода квадратичной аппроксимации [6], положив αk 1=0, Δ α =0,1.
Шаг 7. Вычислить  .
.
Шаг 8. Проверить выполнение условий:

а) если оба условия выполнены, то расчет окончен и X *= Xk+ 1;
б) если хотя бы одно из неравенств не выполнено, то положить k = k +1 и перейти к шагу 3.
Пример 4. Выполнить приближение к локальному минимуму функции f (X)=2 x 12+ x 1 x 2+ x 22 на основе двух итераций в соответствии с методом наискорейшего спуска (Коши).
1. Зададим X 0= 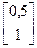 , ε 1=0,1, ε 2=0,15, М =1. Градиент функции в произвольной точке равен
, ε 1=0,1, ε 2=0,15, М =1. Градиент функции в произвольной точке равен 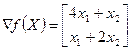 .
.
2. Положим k =0.
3 0. Вычислим  .
.
4 0. Вычислим  . Перейти к шагу 5.
. Перейти к шагу 5.
5 0. Проверим условие k =0<1, перейти к шагу 6.
6 0. Вычислим величину шага вдоль выбранного направления α 0 на основе метода квадратичной аппроксимации [6]. Для этого выполним следующие действия.
1) α 01=0;  ; Значение функции в вычисленной точке равно
; Значение функции в вычисленной точке равно  ;
;
2) α 02= α 01+ Δ α =0,1;

Значение функции в вычисленной точке равно  ;
;
3) Так как f 1> f 2, то α 03= α 01+ 2Δ α =0,2;
 .
.
Значение функции в вычисленной точке равно  ;
;
По имеющимся значениям α 01, α 02 и α 03 и значениям функций f 1, f 2 и f 3 вычисляем значение  , минимизирующее функцию вдоль выбранного направления
, минимизирующее функцию вдоль выбранного направления  .
.
7 0.Вычислим координату точки
 .
.
8 0. Вычислим  .
.
Вычислим  . Полагаем k = k +1=1 и переходим к шагу 3.
. Полагаем k = k +1=1 и переходим к шагу 3.
3 1. Вычислим  .
.
4 1. Вычислим  . Перейти к шагу 5.
. Перейти к шагу 5.
5 1. Проверим условие k =1<2, перейти к шагу 6.
6 1. Вычислим величину шага вдоль выбранного направления α 1 на основе метода квадратичной аппроксимации [6]:  .
.
7 0.Вычислим координату точки
 .
.
Две итерации выполнены. Считаем точку 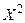 приближением к минимуму функции f (X), то есть
приближением к минимуму функции f (X), то есть  .
.