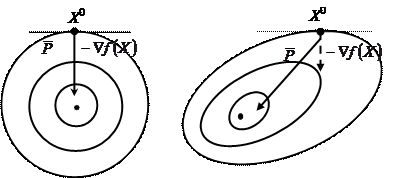
Направление антиградиента функции нескольких переменных приводит точно к точке ее минимума только в определенных случаях [4,5]. Так, например, для функции двух переменных перспективное направление поиска минимума функции совпадает с направлением антиградиента, если линии ее равного уровня представляют собой концентрические окружности (рисунок 7а). В силу нелинейности функций перспективное направление поиска — вектор  может отклоняться от антиградиента (рисунок 7б). Этот вектор может быть вычислен точно с помощью матрицы Гессе или приближенно по системе сопряженных направлений.
может отклоняться от антиградиента (рисунок 7б). Этот вектор может быть вычислен точно с помощью матрицы Гессе или приближенно по системе сопряженных направлений.
Определение 8. Пусть Н — симметрическая матрица размера  . Векторы
. Векторы  называются Н -сопряженными, если
называются Н -сопряженными, если 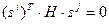 для всех
для всех  .
.
 |
а) б)
Рисунок 7 — Перспективное направление поиска минимума функции.
В методе сопряженных направлений используется тот факт, что минимум квадратичной функции размерности n может быть найден не более, чем за n шагов при условии, что поиск ведется вдоль сопряженных относительно матрицы Гессе направлений. Так как достаточно большой класс целевых функций может быть представлен в окрестности точки минимума своей квадратичной аппроксимацией, описанная идея применяется и для неквадратичных функций.
Метод Флетчера-Ривса.
Пусть дана функция f (X), ограниченная снизу на множестве  и имеющая непрерывные частные производные во всех его точках.
и имеющая непрерывные частные производные во всех его точках.
Требуется найти безусловный минимум функции f (X) на множестве допустимых решений, то есть найти такую точку  , что
, что
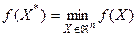 .
.
Стратегия поиска
Стратегия метода состоит в построении последовательности точек { Xk }, k =0,1, …, таких что, 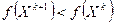 , k=0,1, …. Точки последовательности { Xk } вычисляются по правилу [4,5]:
, k=0,1, …. Точки последовательности { Xk } вычисляются по правилу [4,5]:
 (4.5)
(4.5)
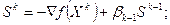 (4.6)
(4.6)
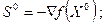 (4.7)
(4.7)
 . (4.8)
. (4.8)
Точка X 0 задается пользователем, величина шага αk определяется для каждого значения k путем минимизации функции f(X) вдоль выбранного направления на основе методов однопараметрической оптимизации.
Вычисление величины 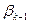 по формуле (4.6) обеспечивает для квадратичной формы
по формуле (4.6) обеспечивает для квадратичной формы  построение последовательности Н -сопряженных направлений
построение последовательности Н -сопряженных направлений 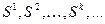 , для которых
, для которых 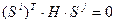 , для всех
, для всех  . При этом в точках последовательности { Xk } градиенты функции f (X) взаимно перпендикулярны, то есть
. При этом в точках последовательности { Xk } градиенты функции f (X) взаимно перпендикулярны, то есть  .
.
Для квадратичных функций f (X) с матрицей Гессе H >0 метод Флетчера-Ривса является конечным и сходится за число шагов, не превышающее n — размерность вектора X.
При минимизации неквадратичных функций метод не является конечным и погрешности в решении задачи минимизации шага вдоль выбранного направления поиска приводят к нарушению не только перпендикулярности градиентов, но и Н -сопряженности направлений.
Алгоритм
Шаг 1. Задать X 0, ε 1>0, ε 2>0, предельное число M. Найти градиент функции в произвольной точке.
Шаг 2. Положить k =0.
Шаг 3. Вычислить 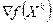
Шаг 4. Проверить выполнение критерия окончания 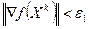 :
:
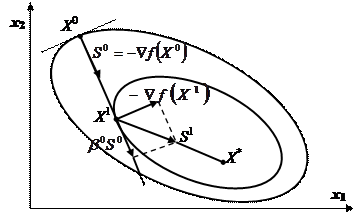 |
Рисунок 8 — Приближение к точке минимума функции на основе метода Флетчера-Ривса.
а) если критерий выполнен, то X *= Xk;
б) иначе перейти к шагу 5.
Шаг 5. Проверить выполнение равенства k ≥ M:
а) если неравенство выполнено, то X *= Xk;
б) иначе, при k =0 перейти к шагу 6, а при k ≥1 перейти к шагу 7.
Шаг 6. Определить 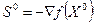 . Перейти к шагу 9.
. Перейти к шагу 9.
Шаг 7. Определить 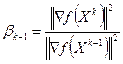
Шаг 8. Определить  .
.
Шаг 9. Вычислить величину αk в соотношении  на основе метода полиномиальной аппроксимации, положив αk 1=0, Δ α =0,1.
на основе метода полиномиальной аппроксимации, положив αk 1=0, Δ α =0,1.
Шаг 10. Вычислить  .
.
Шаг 11. Проверить выполнение условий:

а) если оба условия выполнены, то расчет окончен и X *= Xk;
б) если хотя бы одно из неравенств не выполнено, то положить k = k +1 и перейти к шагу 3.
Пример 5. Выполнить приближение к локальному минимуму функции f (X)=2 x 12+ x 1 x 2+ x 22 на основе двух итераций в соответствии с методом Флетчера-Ривса.
1. Зададим X 0= 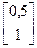 , ε 1=0,1, ε 2=0,15, М =1. Градиент функции в произвольной точке равен
, ε 1=0,1, ε 2=0,15, М =1. Градиент функции в произвольной точке равен 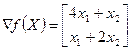 .
.
2. Положим k =0.
3 0. Вычислим  .
.
4 0. Вычислим  . Перейти к шагу 5.
. Перейти к шагу 5.
5 0. Проверим условие k =0<1, перейти к шагу 6.
6 0. Определим  . Перейти к шагу 9.
. Перейти к шагу 9.
9 0.Вычислим величину шага вдоль выбранного направления α 0 на основе метода квадратичной аппроксимации:  . Подробное описание вычислений приведено в примере 4, пункт 6 0.
. Подробное описание вычислений приведено в примере 4, пункт 6 0.
10 0. Вычислим координату точки
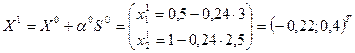 .
.
11 0.Вычислим  .
.
Вычислим  . Полагаем k = k +1=1 и переходим к шагу 3.
. Полагаем k = k +1=1 и переходим к шагу 3.
3 1. Вычислим 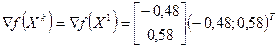 .
.
4 1. Вычислим  . Перейти к шагу 5.
. Перейти к шагу 5.
5 1. Проверим условие k =1<2, при k ≥1 перейти к шагу 7.
7 1. Определим 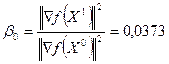 .
.
8 1. Определим

9 1. Вычислим величину шага вдоль выбранного направления α 1 на основе метода квадратичной аппроксимации: 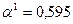 .
.
10 1. Вычислим координату точки
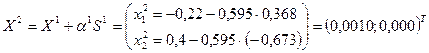 .
.
Две итерации выполнены. Считаем точку 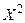 приближением к минимуму функции f (X), то есть
приближением к минимуму функции f (X), то есть 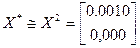 .
.
На рисунке 9 представлен процесс приближения к точке минимума методами Коши и Флетчера-Ривса.
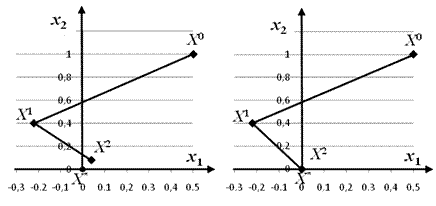
а) б)
Рисунок 9 — Процесс приближения к точке минимума на основе методов: а) Коши; б) Флетчера-Ривса.
Учитывая, что точное значение минимума функции соответствует 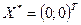 , можно заметить, что метод Флетчера-Ривса позволяет достигнуть точки минимума за две итерации.
, можно заметить, что метод Флетчера-Ривса позволяет достигнуть точки минимума за две итерации.