Метод Дэвидона-Флетчера-Пауэлла.

Пусть дана функция f (X), ограниченная снизу на множестве и имеющая непрерывные частные производные во всех его точках.

Требуется найти безусловный минимум функции f (X) на множестве допустимых решений, то есть найти такую точку , что

.

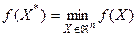Стратегия поиска

Стратегия метода Дэвидона-Флетчера-Пауэлла (Д-Ф-П) состоит в построении последовательности точек { X^k }, k =0,1, …, таких что, 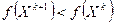, k=0,1, …. Точки последовательности { X^k } вычисляются по правилу [4,5]:

(4.9)

, (4.10)

где A^k – матрица размера , которая вычисляется по правилу:

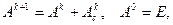(4.11)

, (4.12)

 

где , Е — единичная матрица размера .

Точка X ⁰ задается пользователем, величина шага α^k определяется в результате решения задачи минимизации функции f (X) вдоль выбранного направления S^k на основе методов однопараметрической минимизации.

Формулы (4.11) и (4.12) при аналитическом решении задачи минимизации f (X) обеспечивают построение последовательности { А^k } положительно определенных матриц, таких, что при . Следствием этого для квадратичной функции направления S^k будут Н -сопряженными и, следовательно, алгоритм Д-Ф-П сойдется не более чем за n шагов.

Для неквадратичных функций f (X) алгоритм перестает быть конечным и его сходимость зависит от точности решения задачи минимизации шага вдоль направления поиска. Глобальную сходимость алгоритма можно гарантировать лишь при его обновлении через каждые n шагов, то есть, когда в выражении (4.10)

Построение последовательности { X^k } заканчивается в точке X^k, для которой , где ε ₁ – заданное число, или при k ≤ M (M – предельное число итераций), или при двукратном выполнении двух неравенств , где ε ₂ – малое положительное число.

 

Алгоритм.

Шаг 1. Задать X ⁰, ε ₁>0, ε ₂>0, предельное число итераций M. Найти градиент функции в произвольной точке .

Шаг 2. Положить k =0, А ⁰= Е.

Шаг 3. Вычислить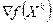

Шаг 4. Проверить выполнение критерия окончания :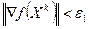

а) если критерий выполнен, то X ^*= X^k;

б) иначе перейти к шагу 5.

Шаг 5. Проверить выполнение равенства k ≥ M:

а) если неравенство выполнено, то X ^*= X^k и расчет закончен.

б) иначе перейти при k =0 перейти к шагу 10, а при k≥1 перейти к шагу 6.

Шаг 6. Вычислить .

Шаг 7. Вычислить .

Шаг 8. Вычислить .

Шаг 9. Вычислить .

Шаг 10. Определить .

Шаг 11. Вычислить величину α^k в соотношении на основе метода полиномиальной аппроксимации, положив α^k ₁=0, Δ α =0,1.

Шаг 12. Вычислить .

Шаг 13. Проверить выполнение условий:

:

а) если оба неравенства выполняются в двух последовательных итерациях с номерами k и k -1, то расчет окончен и X ^*= X^k;

б) в противном случае положить k = k +1 и перейти к шагу 3.

 

Пример 6. Найти локальный минимум функции f (X)=2 x ₁²+ x ₁ x ₂+ x ₂² на основе Д-Ф-П метода. Выполнять вычисления, пока не будет выполнен хотя бы один из критериев окончания расчетов.

1. Зададим X ⁰, ε ₁, ε ₂, М: X ⁰= 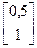, ε ₁=0,1; ε ₂=0,15; М =10. Найдем градиент функции в произвольной точке .

2. Положим k =0, А ⁰= Е= .

3⁰. Вычислим : .

4⁰. Проверим выполнение условия : .

5 ⁰. Проверим выполнение условия k ≥ M: k =0<10= M, переходим к шагу 10.

10⁰. Определим :

11⁰. Вычислим α⁰ на основе метода квадратичной аппроксимации: α⁰ =0,24. Подробное описание вычислений приведено в примере 4, пункт 6 ⁰.

12⁰. Вычислим

13⁰. Проверим условия

:

.

Полагаем k = k +1=1 и переходим к шагу 3.

3¹. Вычислим : .

4¹. Проверим условие : .

5¹. Проверим условие k ≥ M: k =1<10= M, переходим к шагу 6.

6⁰. Вычислим : .

7⁰. Вычислим :

8⁰. Вычислим :

.

9⁰. Вычислим : .

10¹. Определим : .

11¹. Вычислим α¹ на основе метода квадратичной аппроксимации: α¹ =0,618.

12¹. Вычислим

13¹. Проверим условия

:

.

Полагаем k = k +1=2 и переходим к шагу 3.

3². Вычислим : .

4². Проверим условие : .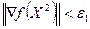

Расчет окончен в точке X ²=(0;0) ^Т. Эта точка является минимумом рассматриваемой функции.

 

 

5 Методы второго порядка. Метод Ньютона.

Пусть дана функция f (X), ограниченная снизу на множестве и имеющая непрерывные частные производные во всех его точках.

Требуется найти безусловный минимум функции f (X) на множестве допустимых решений, то есть найти такую точку , что

.

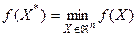Стратегия поиска

Стратегия метода Ньютона состоит в построении последовательности точек { X^k }, k =0,1, …, таких что, 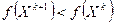, k=0,1, …. Точки последовательности { X^k } вычисляются по правилу [4,5]:

, (5.1)

где X ⁰ — задается пользователем, а направление спуска S^k определяется для каждого значения k по формуле

. (5.2)

Выбор S^k по формуле (5.2) гарантирует выполнения требования 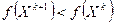при условии, что . Формула (5.2) получена из следующих соображений.

Для определения направления убывания значений функции f (X) и величины шага вдоль выбранного направления метод Ньютона использует информацию о вторых частных производных функции. Разложим функцию f (X) в ряд Тэйлора в окрестности точки X^k:

. (5.3)

В разложении функции f (X) (5.3) отбросим все члены третьего порядка и выше:

(5.4)

Функция F^k представляет собой квадратичную функцию, аппроксимирующую заданную функцию f (X) в точке X^k. Минимум функции F^k является оценкой минимума функции f (X). Определим величину , при которой аппроксимирующая функция F^k достигнет минимального значения. В соответствии с необходимым условием существования экстремума имеем:

. (5.5)

Подставив (5.4) в уравнение (5.5), получим

 

. (5.6)

Решая (5.6) относительно , получим оценку минимума функции f (X):

,

где H (X^k) – матрица Гессе, вычисленная в точке X^k.

Для квадратичных функций метод Ньютона сходится за одну итерацию, для неквадратичных функций сходимость метода определяется точностью решения задачи.

Построение последовательности { X^k } заканчивается в точке X^k, для которой , где ε ₁ – заданное число, или при k ≤ M (M – предельное число итераций), или при двукратном выполнении двух неравенств , где ε ₂ – малое положительное число.

Алгоритм

Шаг 1. Задать начальную точку X ⁰, ε ₁>0, ε ₂>0, предельное число итераций M. Найти градиент функции в произвольной точке и матрицу Гессе H (X).

Шаг 2. Положить k =0.

Шаг 3. Вычислить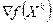

Шаг 4. Проверить выполнение критерия окончания :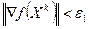

а) если критерий выполнен, то X ^*= X^k;

б) иначе перейти к шагу 5.

Шаг 5. Проверить выполнение равенства k ≥ M:

а) если неравенство выполнено, то X ^*= X^k;

б) иначе перейти к шагу 6.

Шаг 6. Определить матрицу Гессе H (X^k).

Шаг 7. Определить матрицу, обратную матрице Гессе H^-1 (X^k).

Шаг 8. Определить .

Шаг 9. Определить точку .

Шаг 10. Проверить выполнение условий:

:

а) если оба неравенства выполняются в двух последовательных итерациях с номерами k и k -1, то расчет окончен и X ^*= X^k;

б) в противном случае положить k = k +1 и перейти к шагу 3.

 

Пример 7. Определить минимум функции f (X)=2 x ₁²+ x ₁ x ₂+ x ₂². Выполнять вычисления, пока не будет выполнен хотя бы один из критериев окончания расчетов.

1. Зададим X ⁰= 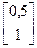, ε ₁=0,1, ε ₂=0,15, М =10.

 

Вычислим градиент функции в произвольной точке и матрицу Гессе .

2. Положим k =0.

 

3 ⁰. Вычислим .

4 ⁰. Вычислим . Перейти к шагу 5.

5 ⁰. Проверим условие k =0<10, перейти к шагу 6.

6 ⁰. Определим матрицу Гессе: .

7 0. Определим матрицу, обратную матрице Гессе:

;

.

8 ⁰. Вычислим

9 ⁰. Вычислим .

10 ⁰. Вычислим .

Вычислим . Полагаем k = k +1=1 и переходим к шагу 3.

3 ¹. Вычислим .

4 ¹. Вычислим .

Точка Х ¹=(0,0) ^Т является точкой минимума функции. Так как рассматриваемая функция является квадратичной, вычислительный процесс сходится за одну итерацию.