Тема: Мера плоского множества
Мера плоского множества 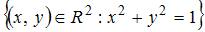 равна
равна  0
0
Решение:
В условии дана окружность радиуса 1, то есть кривая. Ее мера равна нулю.
Тема: Элементы теории множеств
Даны два множества  и
и  . Тогда количество целых значений
. Тогда количество целых значений  ,принадлежащих пересечению множеств А и В равно 4.
,принадлежащих пересечению множеств А и В равно 4.
Тема: Метрические пространства
Функция  заданная на множестве целых чисел …
заданная на множестве целых чисел …

| удовлетворяет всем трем аксиомам метрического пространства |
Тема: Отображение множеств
Прообразом множества  при отображении
при отображении  является
является 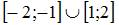
Тема: Элементы теории множеств
Даны два множества: 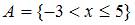 и
и  .Тогда количество целых значений х, принадлежащих объединению множеств А и В, равно …8
.Тогда количество целых значений х, принадлежащих объединению множеств А и В, равно …8
Тема: Мера плоского множества
Мера плоского множества, изображенного на рисунке,

Равна  .
.
Решение:
Мера плоского множества равна площади соответствующей фигуры, то есть для ее определения из площади круга радиуса 4 нужно вычесть площадь круга радиуса 2. Следовательно, мера этого множества равна 
Тема: Метрические пространства
Функция  , где
, где  и
и  , ….
, ….  не удовлетворяет аксиоме треугольника
не удовлетворяет аксиоме треугольника
не удовлетворяет аксиоме симметрии
не удовлетворяет аксиоме тождества
удовлетворяет всем трем аксиомам метрического пространства
Решение:
Функция  не удовлетворяет аксиоме треугольника, например, для точек (-1, -1), (0, 0) и (1, 1).
не удовлетворяет аксиоме треугольника, например, для точек (-1, -1), (0, 0) и (1, 1).
Тема: Отображение множеств
Биективное отображение отрезка  на отрезок
на отрезок 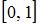 может быть задано функцией …
может быть задано функцией … 
Тема: Метрические пространства
Расстояние между функциями  и
и  пространства всех непрерывных действительных функций, определенных на отрезке
пространства всех непрерывных действительных функций, определенных на отрезке 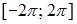 , с метрикой
, с метрикой  , равно…3
, равно…3
Решение: 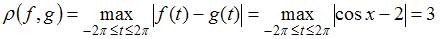
Тема: Отображение множеств
Отображение, действующее из отрезка  на действительную числовую ось и имеющее обратное отображение, может быть задано функцией …
на действительную числовую ось и имеющее обратное отображение, может быть задано функцией … 
Решение:
Функция, действующая из отрезка  на действительную числовую ось и имеющая обратную, должна быть непрерывной и монотонной на
на действительную числовую ось и имеющая обратную, должна быть непрерывной и монотонной на  . Например, это функция
. Например, это функция 
Тема: Мера плоского множества
Мера плоского множества  равна …
равна … 
Решение:
Мера плоского множества  равна площади соответствующей фигуры, изображенной на рисунке:
равна площади соответствующей фигуры, изображенной на рисунке:

Вычислим ее с помощью определенного интеграла. 
Следовательно, мера этого множества равна 
Тема: Отображение множеств
Отображение  действует по правилу:
действует по правилу:  Тогда
Тогда  имеет вид …
имеет вид … 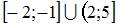
Решение:
Так как  при
при  и
и  при
при  ,то
,то 
Тема: Метрические пространства
Функция  , где
, где  и
и  , …
, …

| не удовлетворяет аксиоме треугольника | ||
| не удовлетворяет аксиоме симметрии | |||
| не удовлетворяет аксиоме тождества | |||
| удовлетворяет всем трем аксиомам метрического пространства |
Решение:
Функция  , где
, где  и
и  , не удовлетворяет аксиоме треугольника, например, для точек (-1, -1), (0, 0) и (1, 1).
, не удовлетворяет аксиоме треугольника, например, для точек (-1, -1), (0, 0) и (1, 1).
Тема: Элементы теории множеств
Даны три множества: 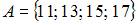 ,
,  и
и 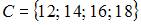 . Тогда число элементов множества
. Тогда число элементов множества  равно …
равно …
| 5 | |
Решение:
Выполним операцию в скобках, то есть определим множество 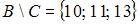 . Теперь выполним объединения
. Теперь выполним объединения  , в результате которого получится множество чисел
, в результате которого получится множество чисел  . Таким образом, множество
. Таким образом, множество 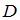 содержит пять элементов.
содержит пять элементов.
Тема: Мера плоского множества
Мера плоского множества  , где А =
, где А = 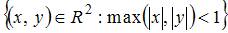 и
и  равна …
равна …

| 
| ||
Решение:
Мера плоского множества 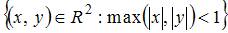 равна площади соответствующей фигуры, то есть квадрата со стороной 2. Мера плоского множества
равна площади соответствующей фигуры, то есть квадрата со стороной 2. Мера плоского множества  равна площади соответствующей фигуры, то есть круга с радиусом 1. Так как круг целиком лежит внутри квадрата, то искомая мера равна
равна площади соответствующей фигуры, то есть круга с радиусом 1. Так как круг целиком лежит внутри квадрата, то искомая мера равна 
Тема: Элементы теории множеств
Даны множества: 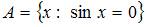 и
и  . Тогда число элементов, принадлежащих их пересечению равно …
. Тогда число элементов, принадлежащих их пересечению равно …
| 3 | |
Решение:
 . Определим множество
. Определим множество 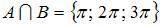 . Получили множество, состоящее из трех элементов.
. Получили множество, состоящее из трех элементов.
Тема: Мера плоского множества
Мера плоского множества 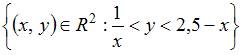 равна …
равна …

| 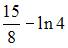
| ||

| |||
Решение:
Мера плоского множества 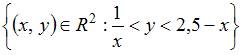 равна площади соответствующей фигуры, изображенной на рисунке:
равна площади соответствующей фигуры, изображенной на рисунке:

Вычислим ее с помощью определенного интеграла. 
Следовательно, мера этого множества равна  .
.
Тема: Элементы теории множеств
Даны два множества:  и
и  . Тогда количество целых значений
. Тогда количество целых значений 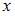 , принадлежащих пересечению множеств
, принадлежащих пересечению множеств 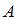 и
и  , равно …
, равно …
| 4 | |
Решение:
Пересечением множеств 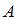 и
и  является промежуток [-1; 3), который содержит четыре целых числа.
является промежуток [-1; 3), который содержит четыре целых числа.
Тема: Метрические пространства
Функция  , где
, где  и
и  , …
, …

| не удовлетворяет аксиоме треугольника | ||
| не удовлетворяет аксиоме симметрии | |||
| не удовлетворяет аксиоме тождества | |||
| удовлетворяет всем трем аксиомам метрического пространства |
Тема: Отображение множеств
Пусть задано отображение  . Тогда
. Тогда  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
По определению прообраза множества  .
.
Тогда 
Тема: Элементы теории множеств
Даны множества:  ,
,  . Тогда число целых чисел, принадлежащих их объединению равно …
. Тогда число целых чисел, принадлежащих их объединению равно …
| 9 | |
Решение:
 .
.
 . Таким образом, объединение содержит девять элементов.
. Таким образом, объединение содержит девять элементов.
Тема: Мера плоского множества
Плоская мера множества  равна …
равна …

| |||
Тема: Метрические пространства
Расстояние между функциями  и
и  пространства всех непрерывных действительных функций, определенных на отрезке
пространства всех непрерывных действительных функций, определенных на отрезке 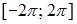 , с метрикой
, с метрикой  , равно …
, равно …

| |||
| – 2 | |||

|
Тема: Отображение множеств
Обратимым на  является отображение …
является отображение …

| 
| ||

| |||
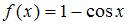
| |||

|
Решение:
Отображение  называется обратимым, если существует отображение
называется обратимым, если существует отображение  такое, что
такое, что  , где
, где 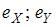 – тождественные отображения на множествах
– тождественные отображения на множествах  и
и  соответственно.
соответственно.
По критерию обратимости: отображение  будет обратимым, если оно инъективно и сюръективно.
будет обратимым, если оно инъективно и сюръективно.
Отображение  на отрезке
на отрезке  не инъективно, например, для точек
не инъективно, например, для точек  и
и 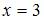 образы совпадают:
образы совпадают:  .
.
Отображения  и
и 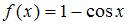 также не инъективны, например, для точек
также не инъективны, например, для точек  и
и  в обоих случаях
в обоих случаях  . Отображение
. Отображение  инъективно (для
инъективно (для  ) и сюръективно (отрезок
) и сюръективно (отрезок  переходит в отрезок
переходит в отрезок  ); обратным для него будет отображение
); обратным для него будет отображение 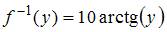
Тема: Мера плоского множества
Мера плоского множества 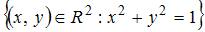 равна …
равна …

| |||

| |||

| |||
Решение:
В условии дана окружность радиуса 1, то есть кривая. Ее мера равна нулю.
Тема: Отображение множеств
Отображение  действует по правилу:
действует по правилу:  Тогда
Тогда  имеет вид …
имеет вид …

| 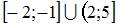
| ||

| |||

| |||

|
Тема: Элементы теории множеств
Даны множества: 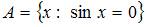 и
и  . Тогда число элементов, принадлежащих их пересечению равно …
. Тогда число элементов, принадлежащих их пересечению равно …
| 3 | |
Решение:
 . Определим множество
. Определим множество 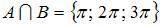 . Получили множество, состоящее из трех элементов.
. Получили множество, состоящее из трех элементов.
Тема: Отображение множеств
Обратимым на  является отображение …
является отображение …

| 
| ||

| |||
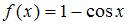
| |||

|
Тема: Элементы теории множеств
Даны два множества:  и
и  . Тогда количество целых значений
. Тогда количество целых значений 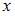 , принадлежащих пересечению множеств
, принадлежащих пересечению множеств 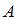 и
и  , равно …
, равно …
Тема: Метрические пространства
Расстояние между функциями  и
и  пространства всех непрерывных действительных функций, определенных на отрезке
пространства всех непрерывных действительных функций, определенных на отрезке 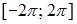 , с метрикой
, с метрикой  , равно …
, равно …

|
Тема: Элементы теории множеств
Даны три множества: 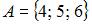 ,
,  и
и  . Тогда число элементов множества
. Тогда число элементов множества  равно …
равно …
| 1 | |
Решение:
Определим множество  и выполним операцию пересечения
и выполним операцию пересечения 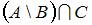 . В результате получится множество
. В результате получится множество  , состоящее из одного элемента.
, состоящее из одного элемента.
Тема: Отображение множеств
Прообразом множества  при отображении
при отображении  является …
является …

| 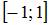
| ||

| |||
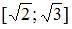
| |||

|
Решение:
Прообразом множества  при отображении
при отображении  являются те точки
являются те точки 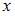 , которые при данном отображении попадают в отрезок
, которые при данном отображении попадают в отрезок  , то есть множество
, то есть множество 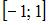 .
.
Тема: Мера плоского множества
Плоская мера отрезка [0; 1], лежащего на оси  в плоскости
в плоскости 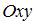 равна …
равна …

| |||
| бесконечности | |||
| несчетна |
Решение:
Плоская мера отрезка [0; 1], лежащего на оси  в плоскости
в плоскости 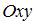 равна нулю.
равна нулю.
Тема: Метрические пространства
Расстояние между точками 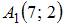 и
и  в метрике
в метрике  , где
, где  и
и  равно 4
равно 4