П.1. Основные утверждения комбинаторики
На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих теми или иными свойствами, располагать элементы одного или нескольких множеств в определенном порядке и т. д. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют "комбинаторные задачи".
Комбинаторика занимается различного рода соединениями, которые можно образовать из элементов некоторого конечного множества. Термин "комбинаторика" происходит от латинского combina - сочетать, соединять.
Комбинаторика - область математики, изучающая комбинации и перестановки различных объектов.
Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.
Правило суммы: пусть имеется n попарно непересекающихся множеств A1, A2, …, An, содержащих m1, m2, …, mn элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m1 + m2 + … + mn.
То есть, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки, можно X+Y способами.
Пример: студент должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение: m1=17, m2=13. По правилу суммы A1UA2=17+13=30 тем.
Кортеж - конечная последовательность (допускающая повторения) элементов какого-нибудь множества.
Правило произведения (Основной принцип комбинаторики): пусть имеется n множеств A1, A2, …, An содержащих m1, m2, …, mn элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т.е. построить кортеж (а1,а2,...,аn), где аiÎАi1 (i = 1, 2, …, n), равно m1·m2·…·mn.
То есть, если на первой полке стоит X книг, а на второй Y, то выбрать одну книгу с первой полки и одну со второй можно X*Y способами.
Пример: сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя - как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z -любые цифры, а X - не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9*10*10=900 вариантов.
п.2. Составление комбинаций из элементов множеств
В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: размещения, перестановки, сочетания. Т.о., основными задачами комбинаторики являются следующие:
1) образование упорядоченных подмножеств - составление размещений;
2) образование упорядоченных множеств, состоящее в установлении определенного порядка следования элементов множества друг за другом, - составление перестановок;
3) образование подмножеств, состоящее в выделении из данного множества некоторой части его элементов, - составление сочетаний.
Размещениями из n элементов по m элементов (m < n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов. Обозначаются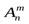 
.
Размещения без повторений: Число размещений из n различных элементов по m элементов вычисляется по формуле:
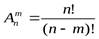(1).
Доказательство: Для того чтобы расположить m элементов в определенном порядке, выберем один из них и будем считать его «первым». Это можно сделать n способами.Оставшееся множество содержит n -1 элемент. Из него выберем один и назовем его «вторым». Для выбора второго элементв имеются n -1 способов. Осталось множество из n -2 элементов. Выбираем из него один и называем его «третьим», что сделать n -2 способами. Продолжив процесс отбора, последний m -й элемент можно выбрать n (m -1) способами. Согласно основному принципу комбинаторики, число всех способов, которыми можно составить размещения, т.е. число размещений равно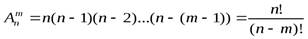 
, ч.т.д.
Размещения с повторениями (n различных элементов, элементы могут повторяться):
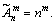(2)
Перестановками из n элементов называются размещения из этих n элементов по n, различающихся только порядком. Перестановки - частный случай размещений. Обозначаются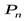 
.
Перестановки без повторений (n различных элементов):
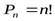(3).
Доказательство: В формуле (1) положим m = n: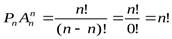 
, ч.т.д.
Перестановки c повторениями (k различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 + … + mk = n, где n - общее количество элементов):
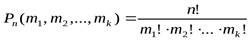(4).
Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом. Обозначаются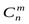 
.
Отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов.
Сочетания без повторений (n различных элементов, взятых по m):
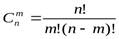(5).
Доказательство: Рассмотрим перестановку из n элементов по m. Их число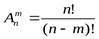 
. Если не считаться с порядком элементов в перестановке из m элементов, то существует m! перестановок, которые неразличимы, т.е. их нельзя отличить от первоначальной перестановки. Поэтому число всех сочетаний из n по m в m! раз меньше числа всех перестановок, т.е. 
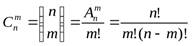, ч.т.д.
Сочетания c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться):
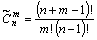(6).