Часть 1
Кинематический и силовой анализ рычажного механизма.
ВВЕДЕНИЕ
Задачи, которые должны быть решены при проектировании, определяются техническим заданием с прилагаемым к нему техническими условиями, определяющими необходимые параметры, которые должны быть выдержаны при проектировании.
Техническое задание
1. Выполнить кинематический синтез схемы центрального кривошипно-ползунного механизма (КПМ) по заданным техническим условиям, включающим структурную схему механизма, и определить координаты характерных точек положения ползуна.
2. Провести кинематический анализ полученной схемы аналитическим и графоаналитическим методами.
3. Провести силовой анализ полученной схемы без учета составляющих сил трения, зависящих от величины усилий, действующих в кинематических парах, аналитическим и графоаналитическим методами.
4. Определить величину уравновешивающего момента с использованием принципа возможных перемещений аналитическим и графоаналитическим методами.
Задание 74, вариант 6, угол 135 
Механизм на рис.1 представляет собой центральный КПМ, преобразующий вращательное движение кривошипа 1 в возвратно-поступательное движение ползуна 3.
Рис.1 Схема кривошипно-ползунного механизма
Механизм имеет следующие исходные данные:
1.Ход поршня 
= 0,25 м.
2.Длина шатуна 
= 1 м.
3.Частота вращения кривошипа n1 = 90 об./мин.
4.Масса шатуна m2 = 5 кг.
5.Масса поршня m3 = 7,5 кг.
6.Угол поворота 
=135 
7.Длина поршня l П = 0,18 м.
8.Перегрузка горизонталная ПГ = 1
9.Перезрузка вертикальная ПВ = 0
10.Сила, действующая на поршень
11.при XB max F’C3 = 400 H
12.при XB ср F’’C3 = 400 H
13.при XB min F’’’C3 = 320 H
14.Число расчетных точек N = 24
15.Диаметр цапфы d = 40 мм.
16.Коэффициенты трения f П = 0,2; fВ = 0,25.
1. Кинематический синтез механизма и определение характерных точек положения ползуна
По известным данным – ходу поршня и длине шатуна - определю длину кривошипа 
, а также координаты двух крайних и среднего положений поршня 
, 
, 
.
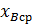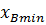Очевидно, что
На рис. 1.1 представлена в масштабе схема механизма в восьми положениях через 450 изменения угла 
1 . На схеме показаны траектории движения точек A, B, S2, где S2 – центр тяжести звена 2.
Рис. 1.1. Схема механизма в восьми положениях
2. Кинематический анализ механизима
Структурный анализ КПМ по Ассуру позволяет представить механизм в виде совокупности первичного механизма (ведущее звено 1 и стойка) и двухповодковой группы (звенья 2 и 3). Кинематический и силовой анализ механизма проводят в соответствии с его структурным составом.
Кинематический анализ КПМ может быть выполнен либо аналитическим, либо графоаналитическим методом.
Аналитическим методом для одного расчетного положения механизма определяются положения, скорости и ускорения звеньев 2 и 3, а также точки S2.
Графоаналитическим методом для того же расчетного положения механизма определяются его кинематические параметры с помощью планов положений механизма, скоростей и ускорений
Аналитический метод расчета
Рис. 2.1 Схема механизма в расчетном положении.
Для решения задачи воспользуемся методом замкнутых векторных контуров. Для этого вдоль каждго звена, составляющего замкнутый контур, направляется вектор. Его угловое положение определяется углом, положительное направление которого отсчитывается в направлении против часовой стрелки от положительной полуоси абсцисс.
На рис.2.1 показаны направления векторов и соответствующие им углы для замкнутого векторного треугольника OBA.
Векторное уравнение замкнутого треугольника имеет вид
Спроектируем векторное уравнение на оси координат x и y:
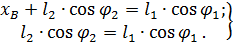
Из первого уравнения можно определить угол 
2. Для принятых расчетных положений механизма он будет
2 = ’2 при xF = +1
2 = 
’2 при xF = -1
где 
- острый угол, определяемый из треугольника OAB:
Из первого уравнения системы определяется координата точки B:
Для оперделения скоростей звеньев 2 и 3 продифференцируеи систму двух уравнений по времени
Или с учетом равенств
будем иметь систему
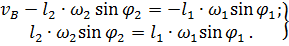
Из второго уравнения системы получим выражение для 
, а из первого – для 
:
Повторное дифференцирование системы уравниений позволяет получить выражения для ускорений звеньев 2 и 3. С учетом равенств
эти выражения имеют вид:
Численные значения кинематический параметров лдя расчетного положения заданного механизма будут следующими:
= 
’2 = 
В радианной мере
Для определения закона движения центра тяжести звена 2 – точки 
составляю новый замкнутый векторный контур 
. Векторное уравнение его имеет вид:
Проектируя уравнение на оси координат, получаю координаты точки
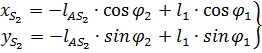
Первая и вторая производные от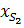 
и 
дадут значения составляющих скорости и ускорения точки :
.
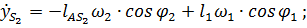
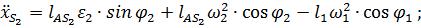
Значения полных векторов скорости и ускорения точки будут
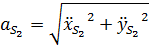
Положение векторов скорости отнсительно оси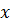 
определяется углом 
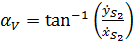при 
при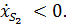 
Аналогично определяется положение вектора ускорения:
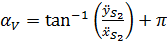при 
при 
Подстановка в полученные выражения численных значений параметров заданного примера дает следующие результаты:
