Рычаг Жуковского является графической интерпретацией метода возможных перемещений.
Н.Е.Жуковский показал, что если векторы всех сил, приложенных к различным точкам звеньев мезанизма, перенести параллельно самим себе в одноименные точки повернутого на 900 плана скоростей, приняв фигуру плана за жесткий рычак, то момент каждой силы относительно полюса плана скоростей будет пропорционален ее мощности, а сумма моментов всех указанных сил будет равна нулю. При этом все моменты, в том числе и уравновешивающий, должен быть заменены парами сил.
Пара сил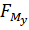 
, заменяющая уравновешивающий момент, будет
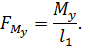
Рычаг Жуковского представлен на рис.3.4, а. План скоростей здесь повернут на 900 по часовой стерлки. Сила 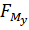произвольно направлена вниз от точки а плана.
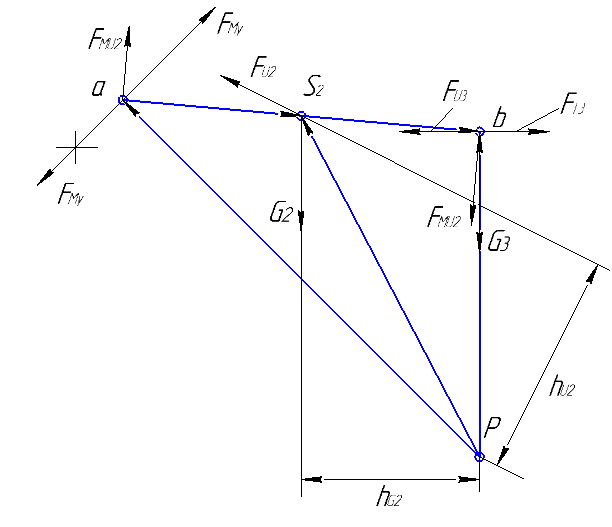
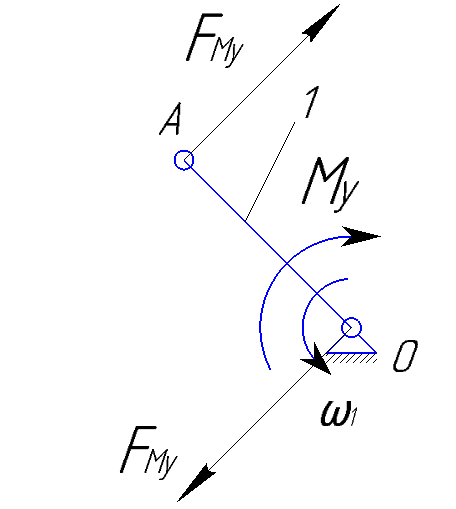
Рис.3.4. Схема первичного механизма и рычаг Жуковского
Сумма моменто сил относительно полюса плана сил р имеет вид
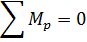
или
Отсюда
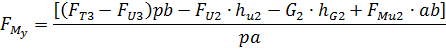
В этом выражении плечи сил определяются из чертежа путем замера.
Как видоно из формулы, величина силы 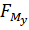не зависит от масштаба построения рычага Жуковского.
Численное значение силы от уравновешивающего момента для рассматриваемого примера равно
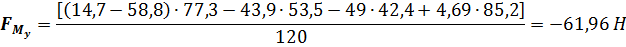
Для определения уравновешивающего момента необходимо полученную силу пренести параллельно самой себе из раычага Жусовского в точку А первичного механизма (рис.3.4,б). Тогда уравновешивающий момент будет положительным и иметь вид
Его величина для рассматриваемого примера
Заключение
Для примера расчета получены следующие разультаты.
1. Вычислены кинематические характеристики ведомых звеньев механизма, позволяющие сделать вывод с рациональности его параметров.
|
|
2. Получены силы и моменты сил, действующие на звенья механизма, позволяющие произветси их расчет на прочность при конструировании.
3. Выявлено влияние сил трения в кинематических парах механизма, позволяющее оценить его КПД.
4. Вычислен уравновешивающий момент, позволяющий щценить потребную мощность для его привода. Для приведенного примера без учета потерь на трение она будет
При подборе электродвигателя следует учесть КПД механизма.
Список литературы
1. Артоболевский И.И. Теория механизма и машин.-М.: Наука, 1988. – 640с.
2. Иосилевич Г.Б., Строганов Г.Б., Маслов Г.С. Прикладная механика. – М.: Высшая школа, 1989. – 351 с.
3. Фралов К.В., Попов С.А. и др. Теория механизмов и машин. – М.: Высшая школа, 1987. – 496 с.
Часть 2
Анализ и синтез планетарного редуктора
Исходные данные для расчета (задание 1047):
1.Стуктурная схема комбинированного редуктора (рис.1а)
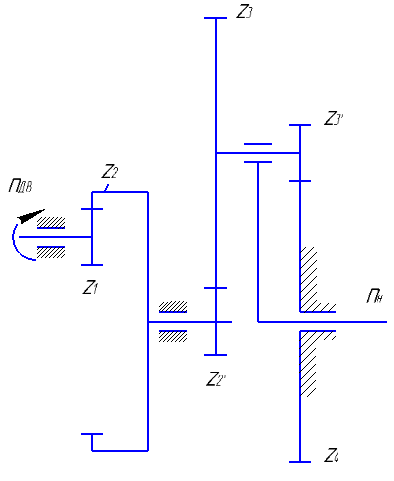
2. Число оборотов на входе редуктора 
=12000 об./мин.
3. Число обротов навыходе редуктора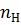 
=250 об./мин.
4.Модуль зубчатых колес передачи m = 8 мм. =0,008 м.
Необходимо выполнить синтез данного планетарного редуктора (найти все zi) беспечивающие работоспособность и заданные передаточные отношения.
Решение. 1.Разбивка общего передаточного отношения по ступеням (первая ступень – рядовая i12 и вторая ступень – планетарная i2’H):
Обычно для такой цилиндрической зубчатой передачи рекомендуется принимать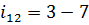 
. Для планетарной ступени 
.
Принимаем 
тогда
2.Подбор чисел зубьев планетарного механизма. Подберём числа зубьев планетарной ступени, обеспечивающие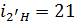 
и соосность осей планетарной ступени по приведенным формулам:
|
|
Тогда
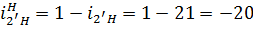
Одновременно
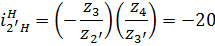
Одновременно возможные варианты значений A,B,C и D:
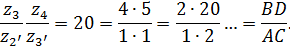
Рассмотрим два варианта подбора чисел зубьев зубчатых колес.
Вариант 1.
С помощью выбора соответствующего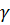 
удовлетворяем рекомендации по выбору 
Принимаем для внешнего зацепления 
для внутреннего – 
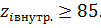Принимаем также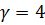 
Тогда
Вариант 2.
Принимаем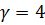
Из двух вариантов вибираем тот, который имеет меньшие габариты, т.е. меньшую сумму зубьев колес, определяющих габариты.
Вариант 1.
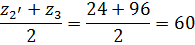
Вариант 2.
Выбираем первый вариант.
Определяем числов зубьев колес 1 и 2 с помощью соотношения 
Принимаем 
Тогда 
3. Определение числа сателлитов. Из условия соседства определим возможное число сателлитов.
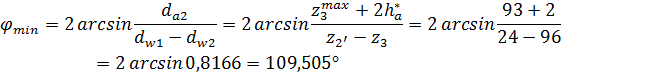
Число сателлитов 
будет
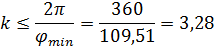
Отсюда 
.
4. Проверка возможности сборки. Условие сборки имеет вид:
При 
т.е. при любом целом p число C будет целом числом, т.е сборка возможно.
5.Кинематический расчет редуктора графоаналитическим метдом. Расчет редуктора графоаналитическим методом выполняется в следующей последовательности.
1.Выбор масштабного коэффициента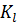 
для построение плана механизма.
2. Построение плана механизма(рис 15,а).
Рис. 15 Кинематический анализ механизма графическим методом
3. Выбор масштабного коэффициента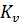 
для построения графика линейных скоростей.
4. Построение графика линейных скоростей (рис. 15,б).
5. Выбор масштабного коэффициента 
для построения плана чисел оборотов
зубчатых колес.
6.Построение плана чисел оборотов (рис. 15,в).
Построение плана зубчатого механизма необходимо начать с определения масштабного коэффициента из равенства:
|
|
где m-модуль зацепления; 
число зубьев первого колеса; 
- длина отрезка, изображающего на плане механизма радиус первого зубчатого колеса.
Размеры других отрезков, изображающих радиусы колес, равны
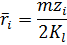
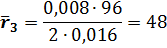
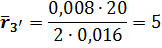
После построения плана редуктора обозначим на чертеже точки кнтакта колес, оси сателлитов и колес (A, B, C, D,E и F).
Масштабный коэффициент для построения графика линейных скоростей определим из соотношения
где 
-скорость точки 
первого зубчатого колеса; 
– длина отрезка, изображающего на графике скорость точки .
Скорость точки первого колеса равна
где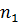 
-число оборотов первого зубчатого колеса 
.
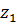Графики линейных скоростей точек зубчатых колес представлены на рис.15,б.
Линия расперделения скоростей каждого колеса строится по двум точкам, скорости которых известны. Так, для первого звена известна скорость точки величина которой определяется по формуле (5)
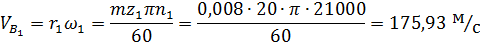
а скорость оси вращения колеса равна нулю. По этим двум точкам строится график распределения окуржных скоростей точек первого звена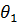 
.
Скорость точки С, лежащей на оси вращения звена 2’ равна нулю. Проводя прямую через точки В’’ и C’ получим линию 
изображающая гафик распределенич окружныз скоростей точек сптеллитов 
. На этой линии располагается конец отрезка D’D’’ скорости точки D, лежащей на линии касанаия колес 
.
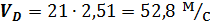
Соединяя точку D’’ с точкой F’ получаем линию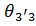 
график окружных скоростей точек звеньев 3 и 3’ относительно водила H.
На линии 
располагается точка E’’ конца отрезка изображающего окружную скорость точки Е, лежащей на оси вращения колеса 3’. Скорость точки F, лежащей на линии касания колес 3’ и 4, равна нулю, так как колесо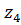 
неподвижно. Проводя прямую через точки E’’ и C’ получим линию 
график распределения окружных скоростей водила Н. Скорость вращения водила Н и звена 3’ равны:
План угловых скоростей зубчаты колес редуктора приведен на рис.15,в.
Масштабный кожффициент для построения плана чисел оборотов определим из равенства
Где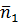 
- размер отрезка, изображающего на плане чисел оборотов первого звена; принимаем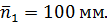 
Построение плана чисел обротов можно начать с отложения на горизонтальной линии отрезка 
соответствующего числу обротов первого звена. Далее из конца этого отрезка (точки 1) проводим линию, параллельную 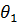, до пересечения ее с вертикальной линией, провденной из начала отрезка (из точки O). Получим точку 
пересечения линии с вертикальной осью. Из этой точки проводим линии, параллельные линиям распределения окружных скоростей точек звеньев на графике линейных скоростей. Отрезок 
пропорционален числу оборотов первого зубчатого колеса, отрезок 
– числу оборотов второго колеса и т.д. Числа оборотов колес можно определить по формуле
где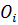 
- длина отрезка, соответствующего числу оборотов 
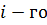звена на плане чисел оборотов.
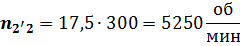
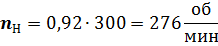
Часть 3