МЕЖДУ ОДИНАКОВЫМИ СПИНАМИ

§ 3. ДИПОЛЬ-ДИПОЛЬНОЕ ВЗАИМОДЕЙСТВИЕ

Полный гамильтониан системы одинаковых взаимодействующих спи­нов в сильном внешнем поле может быть записан в виде

ħ H = ħ(H₀ + H₁). (16)

Основной гамильтониан

ħ H₀ = S_j Z^j = – għ H₀ S_j I^j_z (16a)

описывает энергетические уровни, определяемые выражением ħE⁰_M = – għ Н₀ M, где M — собственное значение оператора

I_z = S_j I^j_z

Гамильтониан возмущения ħ H₁, ответственный за уширение, имеет вид

(16б)

Прежде всего, рассмотрим несколько подробнее взаимодействие между двумя спинами, которые будем обозначать для краткости i и i’. Пусть q и j — полярные координаты вектора r, описывающего их взаимное положение, причем ось z направлена параллельно внешнему полю. Тогда W_ii можно записать в виде

W_{ii '} = { i × i' — 3[ i_z cos q + sin q (i_x cos j + i_y sin j)]x[ i'_z cos q + sin q (i'_x cos y + + i'_y sinj)]}g²ħ²/r³ = { i × i' — 3[ i_z cos q + sin q (i₊ e ^{- i j} + i_- e ^{i j})/2]x[ i'_z cos q + sin q (i₊ e ^{- i j}+ + i_- e ^{i j})/2)]}g²ħ²/r³ = (A+B+C+D+E+F)g²ħ²/r³, (17)

где

A = i'_zi_z (l – 3cos² q),

B = – (l – 3cos² q) (i₊i'_– + i _–i'₊) = (l – 3cos² q)(i_zi'_z– i × i')/2,

C = – 3sinq cosq e ^{- i j} (i_zi'₊ + i ₊i'_z)/2, (18)

D = С* = – 3sinq cosq e ^{i j} (i_zi'_– + i _–i'_z)/2,

E = – 3sin² qe ^{-2 i j} i₊i'₊ /4,

F = E* = – 3sin² qe ^{-2 i j} i _– i'_– /4,.

Запись W в такой форме вызвана следующими причинами. Согласно формуле (14),

c¢¢(w) ~ S¢ | < п | M_x | n’ >| ².

Это приводит к необходимости определить изменение в положении энер­гетических уровней, отвечающих ħ H₀ ,обусловленное наличием ħ H₁. Операторы А, В, С, D, E, F дают качественно различным вклады в это изменение. Упомянутые операторы, действуя на состояние невозмущенного гамильтониана, характеризующееся значениями i_z=т, i ' _z=т', при­водят к следующему изменению этого состояния:

(19)

Рассмотрим теперь энергетический уровень ħE⁰_M = – għ H₀ M, соот­ветствующий гамильтониану (16a). Этот уровень сильно вырожден, так как существует много способов, которыми можно скомбинировать отдельные значения I^j_z =m_j, чтобы получить величину M = S m_j. Таким образом, уровень ħE⁰_M соответствует вырожденному множеству состояний |М>, причем вырождение снимается (по крайней мере частично) возмущением, описываемым гамильтонианом ħ H₁, который расщепляет уровень ħE⁰_M на много подуровней. Согласно первому приближению тео­рии возмущений, вклад первого порядка в расщепление уровня ħE⁰_Mдают лишь те члены гамильтониана возмущения, которые обладают отлич­ными от нуля матричными элементами внутри множества |М >, т. е. те, которые, действуя на состояние |М>, не вызывают изменения величины М. Обращаясь к формуле (19), мы видим, что только те части W, которые отвечают операторам А и В, удовлетворяют этому условию и должны быть сохранены для вычисления энергетических уровней ħ H методом возму­щений.

Член А имеет тот же вид, что и выражение для взаимодействия двух классических диполей и описывает упомянутое в разделе А взаимодействие одного диполя со статическим локальным полем, создаваемым другим дипо­лем. Член В описывает взаимодействие, при котором возможно одновре­менное переворачивание двух соседних спинов в противоположных направ­лениях. Эта часть гамильтониана, названная «переворачивающей» частью, соответствует описанному в разделе А резонансному действию враща­ющегося локального поля. Влияние такого члена, как С, заключается в примешивании к состоянию |М> с невозмущенной энергией ħE⁰_M = – għ H₀ M малой доли состояния |М — 1>. Таким образом, точное соб­ственное состояние ħ H₀ следует представить в виде

| М > + a | М – 1 > + …,

где a — малая величина. Взаимодействие системы спинов с радиочастот­ным полем, приложенным вдоль оси ох, пропорционально I_x = S I^j_x и может индуцировать только переходы с DМ = ± 1. Слабые переходы знежду состоянием, скажем, |M – 2> + малая примесь, энергия которого приблизительно равна – għ H₀ (M —2), и состоянием | М > + a | М – 1 > + … становятся возможными с вероятностью порядка a². Разность энергии между этими состояниями приблизительно равна 2ħw₀. Следовательно, таким переходам на частоте 2w₀ соответствует очень слабая линия, кото­рую обычно трудно наблюдать экспериментально. Легко видеть, что линии сравнимых интенсивностей появляются на частотах 0 и 3w₀.

Доказательство справедливости сохранения в гамильтониане ħ H₁ только членов А и В, которые коммутируют с H₀ обычно называются адиабатической или секулярной частью ħ H₁ и которые впредь будут обо­значаться как ħ H’₀, может быть также дано следующим способом. Так как c¢¢(w) пропорционально фурье-преобразованию G(t)=Sp{ M_x(t)M_x }, то оно может быть вычислено, если известно M_x(t) = е^iHtM_xе^–iHt. В этомслучае M_x(t) удовлетворяет уравнению

(1/i) dM/dt = [ H₀ +H₁, M_x(t) ]. (20)

ОПРЕДЕЛЕНИЕ МОМЕНТОВ

Для резонансной кривой, описываемой нормированной функцией формы f(w) с максимумом на частоте w₀, n-й момент M_n относительно w₀ опреде­ляется выражением

М_n = ∫ (w – w₀)ⁿf(w)dw.

Если f(w) симметрична относительно w₀, то все нечетные моменты равны нулю. Знание моментов дает некоторую информацию о форме резонансной кривой и, в частности, о скорости, с которой она спадает до нуля на крыльях вдали от w₀.

Достоинство метода моментов состоит в том, что моменты могут быть вычислены на основании общих принципов без определения собственных состояний общего гамильтониана ħ H. Прежде чем останавливаться на вычислении моментов, рассмотрим два примера резонансных кривых разном формы. Гауссова кривая описывается нормированной функцией

(24)

для которой легко найти

М₂ = D², M₄ =3D⁴,

М_2n = 1, 3, 5,..., (2n – 1) D²ⁿ,

причем нечетные моменты равны нулю. Полуширина на половине высоты d определяемая соотношением f(w₀ + d) = f(w₀)/2, или ехр(– d²/2D²) = 1/2 оказывается равной

Отсюда видно, что значение второго момента M₂ = D² для гауссовой кри­вой обеспечивает удовлетворительное приближение для ширины линии d.

Другой формой линии, которая часто наблюдается в магнитном резо­нансе, является лоренцева форма, опи­сываемая нормированной функцией

(25)

где d — полуширина на половине высоты.

В этом случае ни второй, ни более высокие моменты не могут быть определены, так как соответствующие интегралы расходятся. Однако иногда теория дает конечные значения для второго и четвертого моментов линий, которые в экспериментально наблюдаемой области имеют лоренцеву форму. В соответствии с конечными значениями M₂ и М₄ далеко на крыльях линии, где невозможно произвести достаточно точные измерения погло­щения вследствие его малой величины, линия должна изменяться более быстро, чем это следует из лоренцевой формы.

Грубая, но удобная пробная модель состоит в описании кривой по формуле (25) внутри интервала |w – w₀|£a, где a>>d и в пред­положении о том, что она равна нулю вне этого интервала. Тогда, прене­брегая членами порядка d/a, найдем

M₂ = D² = 2ad /p, M₄ = 2a³d /(3p), (IV.25a)

откуда, если известны M₂ и M₄ можно вычислить d и a. Поскольку

M₄ /(M₂)² = pa /6d,

упомянутая модель может быть использована лишь, когда теоретическое отношение M₄ /(M₂)² оказывается большим числом., В этом случае

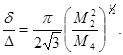(IV.25б)

Ширина на половине высоты значительно меньше, чем среднеквадратичная ширина. С другой стороны, предположение о гауссовой форме линии может быть разумным всякий раз, когда отношение M₄ /(M₂)² порядка 3.