МЕТОД ВЫЧИСЛЕНИЯ МОМЕНТОВ

Основной недостаток метода моментов состоит в том, что важный вклад в значение момента (вклад тем существеннее, чем выше момент) дают крылья кривой, которые на практике не наблюдаются. Необходимо из вычисленных моментов линии магнитного резонанса с центром на ларморовской частоте w =w₀ исключить вклады от сопутствующих линий на частотах w = 0, 2w₀, 3w₀ о которых упоминалось ранее. Легко видеть, что, несмотря на их малую интенсивность (благодаря удаленности от центральной частоты w₀) вклад во второй момент сравним с вкладом от главной линии и тем больше, чем выше порядок момента. Для исключения вкладов от них следует рассматри­вать в гамильтониане возмущения ħ H₁ ответственного за уширение, только его секулярную часть ħ H¢₀, которая коммутирует с H₀ и, следова­тельно, не может отвечать перемешиванию состояний с различными пол­ными М; такое смешивание является причиной появления побочных линий. Таким образом, сокращение дипольного гамильтониана до его секулярной части

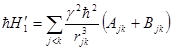
не только упрощает вычисление моментов, но и делает его более точным.

Прежде чем начать расчет, отметим, что линия магнитного резонанса симметрична относительно центральной частоты w₀. Убедимся в правиль­ности этого утверждения. Если | а > и | b > — два собственных состояния ħ(H₀ + H¢₁) с разностью энергии ħ(Е_а — Е_b) = ħw₀ + d_ab, то два состоя­ния | а^~ > и | b^~ >, полученные из | а > и | b > соответственно путем пово­рота всех спинов в обратном направлении, будут также собственными состояниями ħ(H₀ + H¢₁) с ħ(Е_b~ – Е_a~) = ħw₀ + d_ab. Таким образом, каждо­му переходу с частотой w₀ + u соответствует переход равной интенсивности с частотой w₀ – u. Если f(w) — функция формы, то h (u) = f(w₀ + u)— четная функция u. Поскольку моменты кривой пропорциональны про­изводным в начале координат от их фурье-преобразования, мы будем применять для их вычисления формулу (13). Вследствие узости линии ядерного магнитного резонанса можно пренебречь изменением величины w в пределах ширины линии и предположить, что форма линии описывается c¢¢(w)/w, так же как и c¢¢(w). Тогда, поскольку f(w) — нормированная функция формы, (13) может быть переписано в виде

f(w) = A∫ G(t) cos wt dt, (IV.26)

где постоянная A определяется из условия нормировки f(w), а опреде­ленная ранее четная функция G (t) равна Sp{ M_x(t)M_x }. Обратно

G(t) = 2/(pA)∫ f(w) cos wt dw, (IV.27)

Согласно вышеизложенному, в выражении

M_x(t) = е^iHtM_xе^–iHt.

следует вместо H = H₀ + H₁ подставить H = H₀ + H¢₁ что значи­тельно упрощает вычисления. Поскольку H₀ и H¢₁ коммутируют, можно записать

exp{i(H₀ + H¢₁)t} = exp(i H₀ t) exp(i H¢₁ t).

Учитывая, что зеемановский гамильтониан ħ H₀ равен ħw ₀ I_z функцию G (t) можно переписать в виде

(IV.28)

Шпур произведения операторов инвариантен относительно циклической перестановки, поэтому

(IV.28a)

В этом выражении оператор exp(iw ₀ I_zt) определяет поворот на угол w ₀ tвокруг оси z, и, следовательно, можно записать

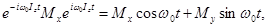
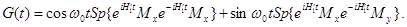(29)

Легко видеть, что второй член в (29) равен нулю, так как поворот спинов на 180°, например вокруг оси ох, не изменяет H¢₁ и M_x но преоб­разует M_у в – M_y.

Заменяя в (27) G (t) на G₁ (t) cosw ₀ t, где

G₁(t)=Sp{ еxp(iH‘₁t)M_xе(–iH‘₁t)M_x }

называется сокращенной функцией автокорреляции, и вводя обозначение

h (u) = f(w₀ + u),

получаем

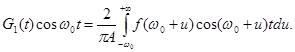
Заменяя нижний предел на – ¥, что допустимо для узких линий, найдем

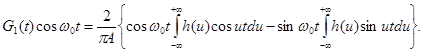
Поскольку h (и) является четной функцией, второй интеграл равен нулю и

G₁(t)=Sp{ еxp(iH‘₁t)M_xе(–iH‘₁t)M_x }

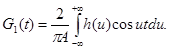(30)

Различные моменты кривой распределения h (и) относительно резонансной частоты w =w₀ определяются выражением

Нечетные моменты равны нулю, а четные определяются формулой

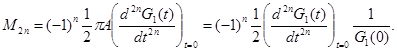(31)

Таким образом, для вычисления моментов резонансной кривой достаточно разложить G₁ (t) в выражении (30) по степеням t. При этом коэффициенты разложения представляют собой шпуры от операторов, которые являются полиномами от H¢₁ и M_x.

Сущность метода заключается в том, что значения упомянутых шпуров не зависят от выбора основных состояний и могут быть вычислены, напри­мер, в представлении, где значения m^j = I^j_z отдельных спинов (поэтому представление называется m^j-представлением) являются хорошими кван­товыми числами. Таким образом, нет необходимости решать проблему отыскания собственных состояний | n > полного гамильтониана. Из опре­деления (30) функции G₁(t) вытекает, что значение ее р-й произ­водной в момент t = 0 определяется выражением

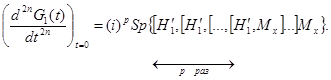(IV.32)

Формула (32) просто находится из дифференциального уравнения

(33)

которому удовлетворяет зависящий от времени оператор

M¢_x(t) = е(iH₁¢t)M_xе(–iH₁¢t)^t.

Решение этого уравнения может быть представлено в виде ряда

M¢_x(t) = M_x + M¢ ⁽¹⁾_x(t) + M¢ ⁽²⁾_x(t) + …+ M¢ ⁽ⁿ⁾_x(t),

отдельные члены, которого получаются методом индукции с помощью соот­ношения

из последнего сразу же следует (32). Из (31) и (32) для первых двух четных моментов находим

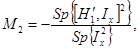(34)

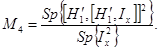(34a)

B (34) M_x заменено полным спином I_x, пропорциональным M_x. По­скольку мы определили гамильтониан в виде ħ H, следует помнить, что эти моменты соответствуют ширинам линии, измеренным в единицах w = 2pn.