Поперечных сил.
Расчёт балки ведём из условия равновесия отдельных дисков. Последовательность расчёта определяется поэтажной схемой (рис.26).
|
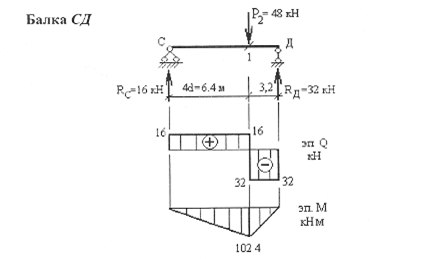
Определение опорных реакций:
Rc-=? ZMD = 0: Rc (4d+2d) - P2-2d = 0
Rc= P2 •2d / (4d+2d) = 48 -2d /6d = 16 kH
RD=? Mс = 0:RD (4d+2d)-P2-4d = 0
Rc= P2•4d / (4d+2d) = 48 -4d /6d =32 kH
Проверка:
ΣY = Rс+ 4 RD-P2 = 16 + 32-48 = 0
Построение эпюр:
Qc = Rc = 16 kH; QLлев = Qc = 16kH
QD = - RD = -32 kH; QLпр = -RD= -32 kH;
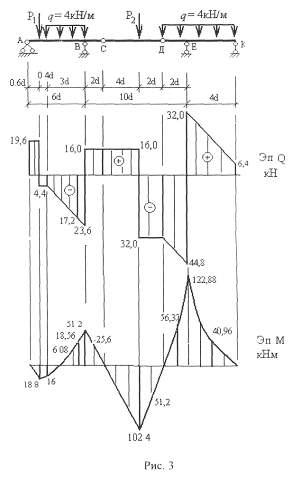
ML = Rc-4d =16-6,4 = 102,4 кН м
Балка А В
Определение опорных реакций:
RA=? ΣMB=0
RA 4d - P,(0,4d+3d) - q-3d-l,5d + Rc• 2d = 0
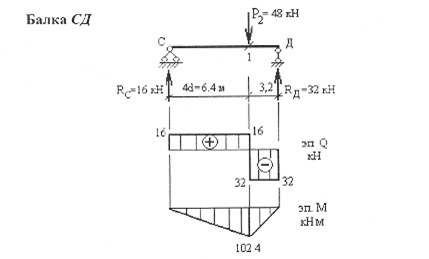
RA = (3,4P1+4,5qd-2Rc)d/4d = (3,4-24 +4,54 1.6-2 16)/4= = 19,6kH
RB=? ΣMA=0;
Rb 4d - R' c (4d + 2d) - q•3d • (3d/2+0,6d+0,4d) – P1 • 0,6d = 0) RB =(6R'c+7,5qd+0,6P1)/4= (6-16 +7,5-4-1,6+0,6-24) / 4= 39,6 kH
Проверка: ΣY- RA+ RB- 2P-3qd = 19,6 + 39,6- 24-3•4•1,6=0
Построение эпюр: Qх = ΣQ4лев = - ΣQхправ QA=RA=19,6kH;
Qsлев = Qa= 19,6kH; Qs пр = RA-P1 = 19,6 -24.0 - 4.4 kH;
Qт= Qsnp= - 4,4 kH:
QBлев= R’с – Rв = 16,0 - 39.6 23.6 kH
Mx = ΣMx лев = - Σ Mxnpaв
М A=0;
Ms = 0.6d RA= 0,6•1,6•19,6 = 18,82 kH∙м
MT = 1.0d•RA-P1•0,4d = 1,6•19,6-24•0,4•1,6 =16.0 kH∙ м
Mв = -Rc • 2d= -16•2•1,6= - 51,2 кН ∙м
Mx = ΣΜхпр = - (Rc (2d +x) - Rb•x + qx2/2) =
= -16(2•l,6+x) + 39,6• x-4x2/2
= -51,2 + 23,6x-2x2
пpи x = 1.5d Mx=-51,2+23,6-l,5d-2(1.5d)2 =- 6.08 kH∙м
при x=2d Mx= ∙ 51,2 +23,6 • 2d -2(2d)2 = 3.84 kH м
Балка ЕК
Определение опорных реакций:
Rt=? ΣMk-0. RE 4d - RD(2d+4d) – q • (2d44d)2/2 = 0
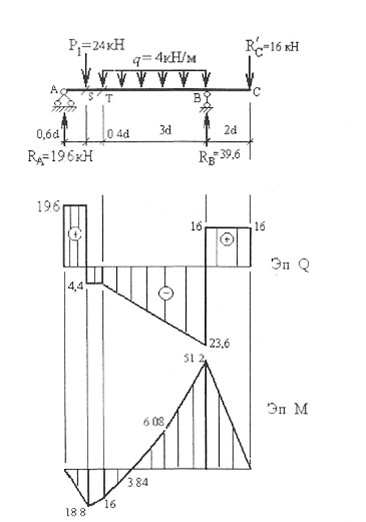
RЕ =(6RD)+8qd)/4 = (6•32 +18 • 4•1.6) /4 = 76.8 kH) RK=0
ΣMЕ =0, Rk 4d- Rс (4d + 2d)- q•4d•2d-RD 2d- q•4d2/2 =0
RK (2R'D - 6qd) /4 = (2 • 32 +6 • 4 1,6) /4 6,4 kH
Проверка ΣY = RΕ- RK- R'D - 6qd = 76,8 - 6,4- 32-6•4•1,6 = 0 Построение эпюр
QD=-R'D=32.0kH,
QEлев = - R'D - q•2d = - 32.0 - 4,0•2•1,6 = - 44,8 kH,
QEпр QEлев + RE = - 44,8 + 76,8 = 32,0 kH;
QK = RK = 6,4 kH,
Мд = 0,
ME =Σ MXлев = -2d RД - q∙ 2d∙d = -2•1,6•32,0 -4,0•2•1.62 =
-122,88kH-м
При X=d
Mx = - dRD - q•d•0,5d = - 1,6•32,0-4,0•0,5•1,62 =
- 56,32 кНм
Мк = 0
Mx= ΣMxnp = - (RK • x + qx2/2) = - 6,4 • x - 2 x2
при x =2d Mx = - 6,4 • 2d - 2(2d)2 = - 40.96 Ш-м
Эпюры изгибающих моментов М и поперечных сил Q для
заданной балки показаны на рис. 3
Построение линий влияния
При построении линий влияния руководствуемся поэтажной схемой (рис. 4). При движении единичного груза Р=1 по балке АВ его действие испытывает только балка АВ. При движении единичного груза Р=1 по балке CD его действие передаётся на балки АВ и ЕК через опоры С и D соответственно.
При движении единичного груза Р=1 по балке ЕК его действие испытывает только балка ЕК

|
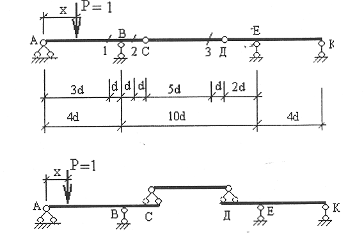
Рис.4
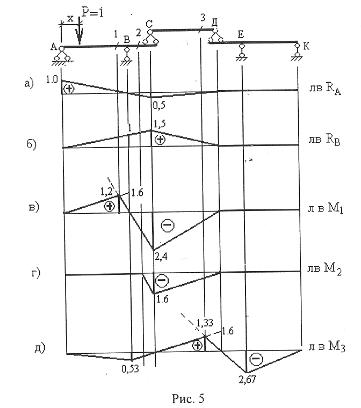
Линия влияния опорной реакции ra (рис. 5а)
При расположении груза Р=1 в т.А нагрузка полностью воспринимается этой опорой и Ra= P=l.
При расположении груза Р=1 в т.В нагрузка полностью воспринимается этой опорой и Ra= 0.
При расположении груза Р=1 в т.С RA= P• 2d/4d =P/2 = 0,5
Линия влияния опорной реакции rb (рис. 56) При расположении груза Р.=1 в т. В нагрузка полностью воспринимается этой опорой и Rb = Р = 1.
При расположении груза Р.=1 в т. А нагрузка полностью воспринимается этой опорой и Rb= 0. При расположении груза Р=1 в т.С rb = P-6d/4d =1,5Р =1,5 Для построения линий влияния в заданных сечениях будем рассматривать движение единичного груза Р=1 сначала слева, а затем справа от сечения. Составляя каждый раз уравнение для определяемого усилия, получим уравнения левой прямой (при движении груза Р=1 слева от сечения) и правой прямой (при движении груза Р=1 справа от сечения) для соответствующей линии влияния.
Линии влияния опорных реакций-см. рис.5(а,б)

|
Линии влияния изгибающих моментов - см. рис.5(в, г, д)
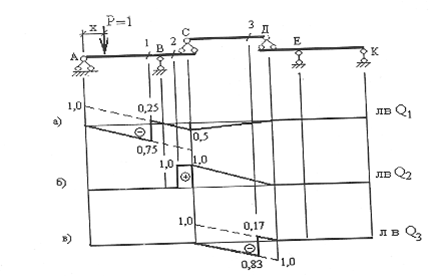
Линия влияния Q1
| Груз Р =1 движется слева от сечения 1 | Груз Р =1 движется справа от сечения 1 |
| Q1 = Σ Q1пр = - RВ л.в. Q1= л.в. RВ - | Q1 = Σ Q1лев= RА л.в. Q1= л.в. RA - |
| уравнение левой прямой | уравнение правой прямой |
Линия влияния Q2
| Груз P= 1 движется слева отсечения 2 | Груз Р= 1 движется справа от сечения 2 |
| M2=ΣQ2пр = 0 л.в. Q2 = 0 - уравнение левой прямой | Q2 =Σ Q2 np= P =1 л.в. Q2 = 1 – уравнения пр.пр. |
Линия влияния Q3
| Груз Р=1 движется слева от сечения 3 | Груз Р=1 движется слева Справа от сечения 3 |
| Q3 =ΣQ3пр = - RД л.в. Q3 = л.в. RД - управление левой прямой | Q3 =ΣQ3лев = - Rс л.в. Q3 = л.в. Rс - управление правой прямой |
Линии влияния поперечных сил- см. рис.6 (а, б, в)
Определение величин опорных реакций, изгибающих моментов и поперечных сил от