Лабораторная работа № 3. Проверка условий. Геометрия на плоскости.
Цель работы: закрепить навыки работы с условным оператором языка Си.
Задачи проверки вхождения точки с заданными координатами в ограниченную область.
Проверка расположения точки с координатами (x,y) относительно прямой.
Пусть уравнение прямой задано в каноническом виде y = ax+b. Тогда, все точки, лежащие на линии прямой подчиняются условию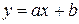 
. Все точки, лежащие левее линии прямой подчиняются условию 
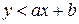, это условие выполняется для точки с координатами 
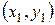. Все точки, лежащие правее линии прямой подчиняются условию 
. Тогда:
· 
.
· 
.
· 
.
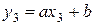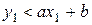Для представленного рисунка составим уравнение прямой по двум заданным точкам: прямая проходит через точки с координатами (0,-1) и (2,0). Найдем коэффициенты уравнения a и b.
Решим систему уравнений:
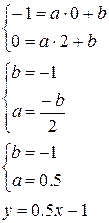
Таким образом, проверить, местоположение точки с координатами (x,y) можно следующим образом:
…
if (y<0.5*x-1) printf(“Точка расположена левее прямой”);
else if(y>0.5*x-1)) printf(“Точка расположена правее прямой”);
else) printf(“Точка расположена на прямой”);
Проверка расположения точки относительно окружности известного радиуса и с заданным центром.
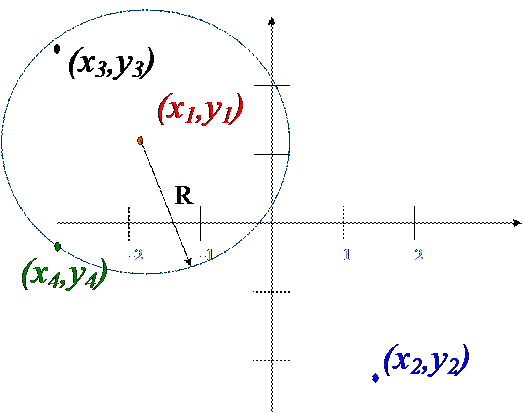
Пусть общее уравнение окружности задано в виде:
R2 = (x-x1) 2+(y-y1) 2
Тогда для точки с координатами (x4,y4) выполняется равенство:
R2 = (x4-x1) 2+(y4-y1) 2
Это уравнение описывает все точки, лежащие на окружности. Для точки с координатами (x2,y2), и для всех точек, лежащих за окружностью, выполняется неравенство:
R2 < (x2-x1) 2+(y2-y1) 2
То есть, радиус данной окружности меньше радиуса окружности с центром в точке (x1,y1), на которой лежит точка с координатами (x2,y2). Соответственно, для точки с координатами (x3,y3) выполняется неравенство -
R2 > (x3-x1) 2+(y3-y1) 2
То есть, радиус данной окружности больше радиуса окружности с центром в точке (x1,y1), на которой лежит точка с координатами (x3,y3).
Построим условия вхождения точки в заданную область:
Уравнение прямой, на которой лежат гипотенузы прямоугольных треугольников, образующих фигуру - y = -x.
Разобьем фигуру на две части. Точка будет считаться принадлежащей фигуре, если она попадет в первую или вторую часть.
Первую (верхнюю часть) можно ограничить следующими условиями:
(y>=-x) и (х<=0) и (y<=2)
Первое условие описывает гипотенузу, второе и третье условие описывают катеты. Условия связаны между собой связками И (логическое умножение)
Вторую (нижнюю часть) можно ограничить условиями:
(y<=-x) и (х>=0) и (y>=-2)
Общее условие для двух частей будет выглядеть следующим образом:
Если (y>=-x) и (х<=0) и (y<=2) или (y<=-x) и (х>=0) и (y>=-2) то «Точка принадлежит заданной области», иначе «Точка не принадлежит заданной области»
Рассмотрим еще один пример:
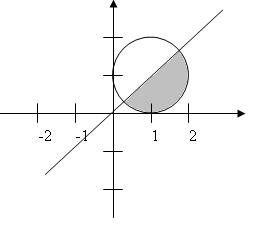
В этом случае уравнение прямой y = x. Уравнение окружности 1 = (x-1) 2+(y-1) 2. Ограниченная область находится правее прямой (y<x) и внутри окружности - 1 > (x-1) 2+(y-1) 2. Тогда общее условие будет выглядеть следующим образом:
Если y<x и 1 > (x-1) 2+(y-1)2 то «Точка принадлежит заданной области», иначе «Точка не принадлежит заданной области»
Порядок выполнения работы
1. Выбрать индивидуальный вариант по номеру в журнале.
2. По выбранному варианту определить условия вхождения точки в заданную область.
3. Составить и записать алгоритм решения задачи
4. Составить программу, реализующую алгоритм:
4.1.Описать входные и выходные данные
4.2.Ввести данные с клавиатуры
4.3.Проверить входные данные
4.4.Проверить условие вхождения точки в заданную область
4.5.Вывести результат проверки на экран
4.6.Вывести личные данные
4.7.Выполнить компиляцию проекта
5. Защитить работу