Раздел 3. ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
Электростатика
· Закон Кулона. Сила F взаимодействия двух точечных неподвижных зарядов q 1 и q 2 прямо пропорциональна величине каждого заряда и обратно пропорциональна квадрату расстояния r между ними:
, или 
, или 
.
Здесь k – постоянная, равная 
; ε0 – электрическая постоянная; e – диэлектрическая проницаемость среды. Для вакуума по определению 
.
· Диэлектрическая проницаемость среды e показывает, во сколько раз взаимодействие зарядов в среде ослабляется по сравнению с вакуумом:
, или 
,
где F – сила взаимодействия зарядов в среде, F 0 – в вакууме; E – напряжённость поля в среде, E 0 – в вакууме.
· Закон сохранения заряда. В замкнутой (точнее, электрически изолированной, то есть не обменивающейся зарядами с окружающей средой) системе алгебраическая сумма электрических зарядов сохраняется:
.
· Напряжённость электростатического поля в данной точке:
,
где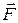 
– сила, действующая на пробный точечный заряд q, помещённый в данную точку поля.
· Сила, действующая на точечный заряд Q, помещенный в точку электрического поля с напряжённостью 
:
.
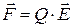· Принцип суперпозиции. Напряжённость поля, созданного в данной точке системой зарядов, равна векторной сумме напряжённостей полей, созданных в этой точке каждым зарядом: 
. В случае непрерывного распределения зарядов: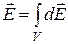 
. Интегрирование ведётся по всему объёму, в котором расположены заряды.
В случае двух электрических полей с напряженностям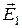и 
и 
модуль результирующего вектора напряженности:
,
где 
– угол между векторами 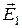и (рис. 3.1).
· Линейная плотность заряда, распределенного по нити (цилиндру) есть величина, равная заряду, приходящемуся на единицу её длины:
.
· Поверхностная плотность заряда, распределённого по поверхности, есть величина, равная заряду, приходящемуся на единицу площади этой поверхности:
.
· Объёмная плотность заряда – это заряд единицы объёма:
.
· Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда
.
· Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:
а) внутри сферы (r<R) E =0;
б) на поверхности сферы (r = R) 
;
в) вне сферы (r>R) .
· Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью
,
где s – поверхностная плотность заряда.
· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью 
заряда (поле плоского конденсатора)
.
Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.
· Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром при r > R, R – радиус цилиндра) нарасстоянии r от нити (или оси цилиндра):
,
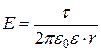где t – линейная плотность заряда.
· Поток вектора напряженности электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
, или 
,
где 
– площадь элемента поверхности; En – проекция вектора напряженности на нормаль 
(рис. 3.2); 
– элементарный поток, пронизывающий малую площадку; – угол между вектором напряженности и нормалью к элементу поверхности;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
.
· Поток вектора напряженности через замкнутую поверхность:
,
где интегрирование ведётся по всей поверхности.
· Вектор электрического смещения – вспомогательная характеристика электрического поля, равная
,
где e – диэлектрическая проницаемость, ε0 – электрическая постоянная, – напряжённость поля. Вектор 
описывает поле только свободных зарядов (в отличие от напряжённости поля , описывающей суммарное поле свободных и связанных, индуцированных зарядов). Соотношение справедливо только дляизотропных диэлектриков.
· Теорема Остроградского – Гаусса. Поток Ф E вектора напряженности через любую замкнутую поверхность:
,
где 
– алгебраическая сумма зарядов (свободных и связанных), заключенных внутри замкнутой поверхности; п – число зарядов.
· Теорема Остроградского – Гаусса для электрического смещения . Поток Ф D вектора электрического смещения через любую замкнутую поверхность равен
,
где 
– алгебраическая сумма свободных зарядов, заключенных внутри замкнутой поверхности; п – число зарядов.
· Циркуляция векторного поля –это интеграл по замкнутому контуру вектора напряжённости поля. Для электростатического поля циркуляция напряжённости:
, или 
,
где 
– проекция вектора напряженности в данной точке контура на направление касательной к контуру в той же точке, a – угол между вектором напряженности и элементом 
контура (рис. 3.3).
· Теорема о циркуляции: циркуляция вектора напряжённости электростатического поля по произвольному замкнутому контуру равна нулю:
.
· Энергия взаимодействия двух точечных зарядов q 1 и q 2, находящихся на расстоянии r друг от друга:
,
где e – диэлектрическая проницаемость среды; ε0 – электрическая постоянная.
· Потенциал данной точки поля – это энергия единичного положительного точечного пробного заряда, помещённого в данную точку поля:
.
Потенциал данной точки поля численно равен работе по перемещению единичного точечного пробного положительного заряда из данной точки поля на бесконечность: 
. Потенциал бесконечно удалённой точки считается равным нулю. Если точечный заряд q поместить в точку поля, имеющую потенциал φ, то энергия заряда равна 
.
· Потенциал электрического поля, создаваемый точечным зарядом q на расстоянии r от заряда:
.
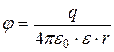· Потенциал электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы
- внутри и на поверхности сферы (
): 
;
- вне сферы (r>R): .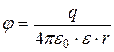
Здесь e – диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
· Принцип суперпозиции. Потенциал, созданный в данной точке системой зарядов qi, равен алгебраической сумме потенциалов полей, созданных в данной точке каждым зарядом системы в отдельности:
.
В случае непрерывно распределённых зарядов: 
. Здесь интеграл берётся по всей области, где локализованы заряды, а потенциал dφ создаётся зарядом 
, локализованным в элементарном малом объёме dV; ρ – объёмная плотность заряда.
· Потенциал электрического поля, созданного системой п точечных зарядов в данной точке, равен алгебраическойсуммепотенциалов j 1, j 2,..., jn полей, создаваемых отдельными точечными зарядами q 1, q 2,..., qn:
.
· Потенциальная энергия W взаимодействия системы точечных зарядов q 1, q 2,..., qn:
,
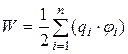где 
– потенциал поля, создаваемого всеми (п– 1) зарядами (за исключением i -го) в точке, где расположен заряд qi. Энергия системы зарядов равна работе, которую эта система зарядов совершает при удаленииих относительно друг друга в бесконечность: 
.
· Связь потенциала 
и напряженности электрического поля:
, или 
.
Здесь 
. Интегрирование производится по любому контуру, соединяющему точки 1 и 2; 
– проекция вектора напряженности 
в данной точке контура на направление касательной к контуру в той же точке. В проекциях на любую ось:
.
В случае электрического поля, обладающего сферической симметрией:
, или 
.
В случае однородного поля (когда напряженность в каждой точке поля одинакова как по модулю, так и по направлению:
,
где j 1 и j 2 – потенциалы точек двух эквипотенциальных поверхностей; d – расстояние между этими поверхностями вдоль силовой линии поля.
· Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал j 1, в другую, имеющую потенциал j 2, равна
, или 
,
где – проекция вектора напряженности на направление перемещения; dl – перемещение. В случае однородного поля:
,
где l – перемещение; 
– угол между векторами напряжённости поля 
и перемещения 
.
· Диполь (электрический диполь) – система двух одинаковых по величине противоположных по знаку точечных зарядов q и – q (рис. 3.4). Плечо диполя 
– вектор, начинающийся на отрицательном заряде и оканчивающийся на положительном. Диполь называетсяточечным, если его плечо l много меньше расстояния r до точек наблюдения (l<<r).
· Дипольный момент электрического диполя – вектор, равный произведению модуля заряда диполя на плечо диполя:
.
· Напряженность поля точечного диполя в точке А (рис. 3.4) с радиус-вектором 
, образующим угол α с вектором 
дипольного момента:
, или 
.
· Потенциал поля точечного диполя в точке А (рис. 3.4) с радиус-вектором , образующим угол α с вектором дипольного момента:
, или 
.
· Механический момент сил, действующий на диполь в электрическом поле:
; или 
,
где 
– электрический дипольный момент, – напряжённость поля, α – угол между ними.
· Сила, действующая на диполь в неоднородном электрическом поле. В неоднородном электрическом поле, кроме механического момента (пары сил), на диполь действует сила, проекция которой на произвольную ось OX равна:
,
где pe – дипольный момент,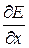 
– быстрота изменения поля вдоль оси OX, α – угол между дипольным моментом и вектором напряжённости. Если угол α острый, диполь втягивается в область сильного поля, если тупой – выталкивается.
· Потенциальная энергия диполя в электрическом поле:
,
где – электрический дипольный момент, – напряжённость поля,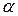 
– угол между ними.
· Электрическая ёмкость проводника:
,
где 
– заряд, сообщенный проводнику; 
– изменение потенциала проводника, вызванное этим зарядом. Или: ёмкость равна отношению заряда проводника к его потенциалу: 
. (Считается, что потенциал бесконечно удалённой точки равен нулю.)
· Электрическая ёмкость уединенной проводящей сферы (шара) радиусом R,находящейся в бесконечной среде с диэлектрической проницаемостью ε:
.
Если сфера полая и заполнена диэлектриком, то электроемкость её от этого не изменяется.
· Электрическая ёмкость конденсатора:
,
где 
– заряд конденсатора; 
– разность потенциалов обкладок конденсатора.
· Связь между напряженностью 
поля плоского конденсатора и напряжением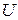 
на нём:
,
где d – расстояние между обкладками.
· Электрическая ёмкость:
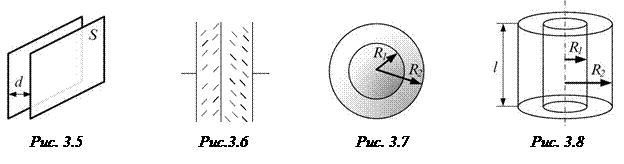- плоского конденсатора (рис. 3.5):
,
где S – площадь пластин (каждой пластины); d – расстояние между ними (d много меньше размера пластин); ε – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами;
- плоского конденсатора, заполненного п слоями диэлектрика толщиной 
каждый с диэлектрическими проницаемостями 
, (слоистый конденсатор, рис. 3.6):
;
- сферического конденсатора (две концентрические сферы радиусами R 1и R 2, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε, рис. 3.7):
;
- цилиндрического конденсатора (два коаксиальных цилиндра длиной l и радиусами R 1и R 2, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε, рис. 3.8) при условии l >> R:
.
· Общая ёмкость при параллельном соединении конденсаторов:
,
где п – число конденсаторов. Для двух конденсаторов: 
. Для п одинаковых конденсаторов с электроёмкостью С 1 каждый: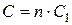 
.
· Общая ёмкость при последовательном соединении конденсаторов:
,
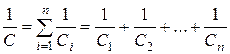где п – число конденсаторов. Для двух конденсаторов: 
. Для п одинаковых конденсаторов с электроёмкостью С 1 каждый: 
.
· Энергия заряженного проводника выражается через заряд q, потенциал φ и электрическую ёмкость С проводника следующими соотношениями:
.
· Энергия заряженного конденсатора
где С – электрическая ёмкость конденсатора, q – его заряд, U – разность потенциалов на его пластинах.
· Объёмная плотность энергии – это энергия единицы объёма:
, или 
.
· Объёмная плотность энергии электростатического поля:
, или 
,
где Е – напряжённость поля, D – электрическое смещение.
Электрический ток
· Сила тока – отношение заряда 
, прошедшего через сечение проводника, к промежутку времени 
, за которое заряд был перенесён:
.
Сила тока – производная заряда по времени. Только в случае, когда ток постоянный, можно использовать формулу
,
где 
– заряд, прошедший через сечение проводника за время 
.
· Плотность электрического тока – это сила тока 
, приходящаяся на единицу площади сечения проводника 
:
, или, точнее, 
.
· Плотность электрического тока – это вектор, равный:
;
,
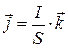Здесь 
– концентрация свободных носителей заряда в проводнике, 
– заряд каждой частицы, 
– средняя скорость их направленного движения, 
– единичный вектор, сонаправленный с направлением движения положительных носителей заряда.
· Сопротивление однородного проводника
,
где ρ – удельное сопротивление вещества проводника; l – его длина; S – его сечение.
· Проводимость G проводника и удельная проводимость γ вещества
; 
.
· Зависимость сопротивления R и удельного сопротивления ρ от температуры:
; 
,
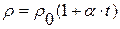где ρ 0 (R 0) – удельное сопротивление (сопротивление) при температуре 00С; t –температура (по шкале Цельсия); 
– температурный коэффициент сопротивления.
· Сопротивление при последовательном соединении проводников:
· Сопротивление при параллельном соединении проводников:
.
Здесь Rk – сопротивление k- го проводника; N – число проводников.
· Электродвижущая сила (ЭДС) численно равна работе сторонних сил по перемещению единичного заряда по замкнутой цепи. Или: ЭДС равна работе сторонних сил по перемещению точечного заряда по замкнутой цепи, отнесённой к величине этого заряда:
.
· Закон Ома:
- для неоднородного участка цепи (участка, содержащего ЭДС):
;
- для однородного (не содержащего ЭДС) участка цепи:
;
- для замкнутой цепи: 
.
Здесь (φ 1– φ 2) – разность потенциалов на концах участка цепи; ε – ЭДС источника тока, U – напряжение на участке цепи; R – сопротивление цепи (участка цепи); r – внутреннее сопротивление источника тока.
· Первое правило Кирхгофа. Алгебраическая сумма токов, сходящихся в узле, равна нулю:
,
причём токи, заходящие в узел, надо брать в этой сумме с положительным знаком, выходящие из узла – с отрицательным. Здесь N – число токов, сходящихся в узле.
· Второе правило Кирхгофа. Алгебраическая сумма напряжений на всех участках любого замкнутого контура равна алгебраической сумме ЭДС, включенных в данный контур:
.
Здесь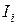 
– сила тока на i- мучастке; 
– сопротивление i- тогоучастка;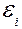 
– ЭДС источников тока на i- мучастке; п – число участков, содержащих сопротивления; k – число участков, содержащих источники тока. Правило знаков: если направление тока на данном участке совпадает с направлением обхода контура, то произведение 
надо брать с положительным знаком; иначе – с минусом. Если ЭДС при обходе контура проходим от минуса к плюсу, то 
надо брать с плюсом; иначе – с минусом.
· Работа, совершаемая электростатическим полем и сторонними силами на участке цепи постоянного тока за время t:
.
В случае непостоянного тока работа равна:
.
· Мощность тока
.
· Закон Джоуля-Ленца для постоянного тока:
,
где Q – количество теплоты, выделяющееся в участке цепи при протекании постоянного тока за время t. В случае непостоянного тока:
; 
.
Здесь 
– мгновенная сила тока. Закон Джоуля-Ленца справедлив при условии, что участок цепи неподвижен и в нём не совершаются химические превращения
· Коэффициент полезного действия источника тока (см.рис. 3.9):
.
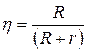Раздел 4. ЭЛЕКТРОМАГНЕТИЗМ
Магнитное поле
· Закон Био-Савара-Лапласа: индукция 
, созданная элементом тока 
точке А (рис. 4.1):
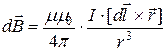, или 
.
Здесь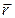 
– радиус-вектор точки, в которой нужно рассчитать индукцию поля (вектор проводится от элемента тока к точке); 
– угол между радиус-вектором 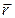и элементом тока ; m – магнитная проницаемость вещества;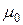 
– магнитная постоянная; 
– вектор, равный по модулю элементу длины dl проводника и совпадающий по направлению с током; I – сила тока.
· Магнитная проницаемость среды μ показывает, во сколько раз индукция 
магнитного поля в среде больше индукции 
в вакууме:
.
· Напряжённость магнитного поля 
– это вспомогательная характеристика магнитного поля, описывающая только поле макротоков (токов проводимости), в отличие от индукции 
магнитного поля. Связь между индукцией 
и напряжённостью для однородной изотропной среды:
.
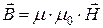Для вакуума (m =1):
.
Для поля соленоида (тороида) с сердечником из ферромагнетика магнитную проницаемость 
следует определять, используя график зависимости В от Н для конкретного вида магнетика, а затем по формуле:
.
· Магнитный момент контура с током:
,
где I – сила тока в контуре, S – его площадь, 
– единичный вектор нормали к контуру (рис. 4.2). Если контур имеет N витков, то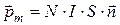 
.
· Индукция магнитного поля В – отношение максимального вращающего момента М max сил, действующих на контур, к магнитному моменту 
контура:
.
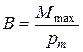· Момент силы (механический вращающий момент), действующий на магнитный момент 
в магнитном поле с индукцией :
, или 
,
где – угол между вектором магнитной индукции и магнитным моментом магнитной стрелки или витка с током (рис. 4.3).
· Принцип суперпозиции: если в данной точке пространства различные источники создают магнитные поля, магнитные индукции которых равны 
, 
…, 
, то результирующая индукция поля в этой точке равна:
.