ЧАСТЬ 1. Общая теория статистики
Задача 1
Имеются данные по 19 предприятиям отрасли:
| Среднегодовая стоимость основных фондов, млн. руб. | 4,9 | 4,5 | 7,0 | 1,0 | 3,0 | 7,0 | 2,0 | 3,9 | 3,3 | 2,8 |
| 6,5 | 6,6 | 2,0 | 4,7 | 2,7 | 3,3 | 3,0 | 3,1 | 3,1 | ||
| Производство продукции за отчетный год, млн. руб. | 4,4 | 5,6 | 12,9 | 1,6 | 3,2 | 9,6 | 1,5 | 4,2 | 6,4 | 2,8 |
| 9,4 | 11,9 | 2,5 | 3,5 | 2,3 | 1,3 | 1,4 | 3,0 | 2,5 |
Проведите аналитическую группировку. По каждой группе подсчитайте: 1) число заводов; 2) стоимость основных фондов в среднем на одно предприятие; 3) производство продукции всего и в среднем на одно предприятие. Сделайте выводы.
Решение.
При 19 наблюдениях целесообразно образовать 3группы, группировочный признак – среднегодовая стоимость основных фондов.
Величина интервала определяется по следующей формуле:

где xmax, xmin – соответственно максимальное и минимальное значение признака в ряду распределения;
k – число групп.

Статистическая таблица группировки предприятий по среднегодовой стоимости основных фондов
| Группа предприятий по среднегодовой стоимости основных фондов, млн. руб. | Число предприятий в группе | Среднегодовая стоимость основных фондов, млн. руб. | Производство продукции за отчетный год, млн. руб. | ||
| общая по группе | средняя по группе | общая по группе | средняя по группе | ||
| 1,0 – 3,0 | 7,7 | 1,93 | 7,9 | 1,98 | |
| 3,0– 5,0 | 39,6 | 3,60 | 38,3 | 3,48 | |
| 5,0 - 7,0 | 27,1 | 6,78 | 43,8 | 10,95 | |
| Итого | 74,4 | - | 90,0 | - |
Данные таблицы показывают, что с увеличением среднегодовой стоимости основных фондов систематически в среднем по группе возрастает и объем производства продукции, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.
Задача 2
Вычислите средние по следующим признакам:
| Предприятие | Фактический выпуск продукции за период, тыс. руб. | Выполнение плана по выпуску продукции за период, % | Выпуск продукции на одного рабочего, тыс. руб. | Продукция высшего сорта, % |
| 125,0 | 0,26 | 94,2 | ||
| 110,0 | 0,22 | 98,6 | ||
| 105,0 | 0,18 | 95,0 |
Решение:
Фактический выпуск продукции (Q):

где w – выпуск продукции на одного рабочего;
T – численность рабочих.
Средний фактический выпуск продукции одного предприятия по формуле средней арифметической простой:

Относительная величина выполнения плана по выпуску продукции определяется по формуле:

Средний процент выполнения планового задания по выпуску продукции по формуле средней гармонической взвешенной:

Выпуск продукции на одного рабочего

где w – выпуск продукции на одного рабочего;
Q – выпуск продукции;
T – численность рабочих.
Средний выпуск продукции на одного рабочего по формуле средней гармонической взвешенной:

Процент продукции высшего сорта по формуле:

Средний процент продукции высшего сорта по формуле средней арифметической взвешенной:


Задача 3
На предприятии, где число рабочих составляет 1000 человек, было проведено выборочное обследование возраста рабочих. Методом случайного бесповторного отбора было отобрано 50 человек. Результаты обследования следующие:
| Возраст рабочих, лет | Число рабочих |
| До 30 | |
| 30–40 | |
| 40–50 | |
| Свыше 50 | |
| Итого |
В каких пределах находится доля рабочих возрастом свыше 50 лет во всей генеральной совокупности? Ответ дать с вероятностью 0,997.
Решение:
Границы генеральной доли определяются по формуле:

где – p генеральная доля;
Δw – предельная ошибка выборочной доли.
Для собственно-случайной выборки с бесповторным способом отбора предельная ошибка выборки доли единиц, обладающих заданным свойством, рассчитывается по формуле:

где w – доля единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не обладающих заданным свойством;
t – коэффициент доверия, при Ф(t) = 0,997 t = 3.
Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой:

где m – число единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Выборочная доля:


Доверительный интервал генеральной доли (р):
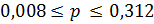

С вероятностью 0,997 можно утверждать, что границы доли рабочих возрастом свыше 50 лет находятся в пределах от 0,8% до 31,2%.
Задача 4
Имеются следующие данные о розничном товарообороте магазина:
| Месяцы | Январь | Февраль | Март | Апрель | Май | Июнь |
| Розничный товарооборот, тыс. руб. |
Используя аналитическое выравнивание по параболе второго порядка, определите ожидаемый объем товарооборота в июле. Рассчитайте за полугодие: а) средний размер розничного товарооборота; б) среднемесячный абсолютный прирост; в) средний темп роста.
Решение:
Трендовое уравнение параболы второго порядка имеет вид:

При Σt=0 система нормальных уравнений для нахождения параметров уравнения:

Вспомогательная таблица для расчета параметров
| Годы | Розничный товарооборот, тыс. руб. | Обозначения временных дат, t | t2 | t3 | t4 | yt | yt2 |
| Январь | -3 | -27 | -255 | ||||
| Февраль | -2 | -8 | -172 | ||||
| Март | -1 | -1 | -87 | ||||
| Апрель | |||||||
| Май | |||||||
| Июнь | |||||||
| Итого |



Трендовое уравнение имеет вид:

Ожидаемый объем товарооборота в июле:

Если выявленная тенденция сохранится, то объем товарооборота в июле составит 91,95 тыс. руб.
а) средний размер розничного товарооборота:

б) среднемесячный абсолютный прирост:

где yn, y1– конечный и начальный уровни ряда.

в) средний темп роста

За исследуемый период среднемесячный розничный товарооборот магазина составил 87,3 тыс. руб. Выявлена положительная динамика, за исследуемый период ежемесячное увеличение розничного товарооборота магазина составляло в среднем 1,2 тыс. руб. или 1,4%.
Задача 5
Имеются следующие данные о продаже картофеля на рынках города за два месяца:
| Рынок | Февраль | Март | ||
| Количество, т | Средняя цена 1 кг, руб. | Количество, т | Средняя цена 1 кг, руб. | |
На основе приведенных данных определить: 1) динамику средней цены на картофель (индекс переменного состава); 2) среднее изменение цены на картофель (индекс постоянного состава); 3) влияние изменения структуры продажи картофеля на динамику средней цены (индекс структурных сдвигов). Сделайте выводы.
Решение:
Вспомогательная таблица для расчета индексов переменного состава, постоянного состава и структурных сдвигов
| Рынок | Количество, т | Средняя цена 1 кг, руб. | Товарооборот, тыс. руб. | Расчетная величина, тыс. руб. | |||
| Февраль | Март | Февраль | Март | Февраль | Март | ||
| q0 | q1 | p0 | p1 | 
| 
| 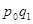
| |
| Итого | – | – |
Индекса переменного состава:

Индекс цен постоянного состава

Индекс цен структурных сдвигов:

На основе этой системы индексов можно сделать вывод, что средняя цена на картофель в марте по сравнению с февралем увеличилась на 3,3%.
За счет изменения структуры цены, средняя цена возросла на 4,8%, за счет изменения доли каждого рынка (структурных сдвигов) в общем объеме товарооборота средняя цена снизилась на 1,5%.
ЧАСТЬ 2. Социально-экономическая статистика