Уровень капиталовооруженности и Золотое правило

Теперь предположим, что субъект, вырабатывающий экономическую по­литику, может просто выбрать национальную норму сбережений и соответст­венно определенное устойчивое состояние.

Делая выбор в пользу того или иного устойчивого состояния, политик преследует цель максимизации экономического благосостояния общества. Для самих же членов общества важно лишь количество товаров и услуг, которое они могут потреблять. Поэтому политик, заинтересованный в экономическом благосостоянии, захочет выбрать устойчивое состояние с наивысшим уровнем потребления. Уровень накопления капитала, обеспечивающий устойчивое со­стояние с наивысшим уровнем потребления называется Золотым уровнем на­копления капитала и обозначается k**.

Чтобы определить k**, необходимо сначала определить потребление на одного работника в устойчивом состоянии, а затем выяснить, какое из устойчи­вых состояний обеспечивает наибольшее потребление.

Чтобы найти потребление в устойчивом состоянии, начнем с уравнения

 

y = c + i

 

Преобразуем его в c = y – i.

Заменим значение у и i на их величины в условиях устойчивого уровня капиталовооруженности: y = f(k*), т. к. в устойчивом состоянии капиталово­оруженность не изменяется, а инвестиции равны выбытию, т. е. i = dk*. Под­ставим эти выражения и получим:

 

c* = f(k*) – dk*

 

Это уравнение показывает, что устойчивый уровень потребления есть разность между выпуском и выбытием капитала в устойчивом состоянии. На рис. 3.6 показан выпуск продукции f(k*) и выбытие dk* в виде функции от ус­тойчивой капиталовооруженности. На графике видно, что существует только один уровень капиталовооруженности – уровень золотого правила k**, при ко­тором душевое потребление достигает максимума.

 

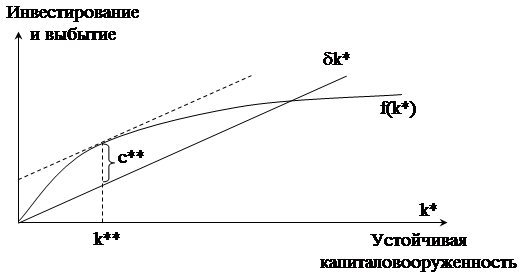Рис. 3.6 - Устойчивый уровень потребления

 

Если капиталовооруженность меньше уровня по Золотому правилу, рост запасов капитала вызывает рост производства, превышающий увеличение вы­бытия (потребление растет). Если объем капитала превышает уровень Золотого правила, дальнейший рост капиталовооруженности уменьшает потребление, так как рост выпуска продукции оказывается меньше, чем прирост выбытия ка­питала. При капиталовооруженности на уровне Золотого правила потребление достигает максимума.

К этому же выводу мы можем прийти другим путем. Увеличение устой­чивой капиталовооруженности с k* до k*+ 1 увеличит выпуск продукции с f(k*) до f(k*+ 1).

 

f(k*+ 1) – f(k*) = MPK – предельный продукт капитала

 

Увеличение капиталовооруженности на 1 единицу увеличивает выбытие на d. Значит, увеличение потребления от дополнительной единицы составит МРК – d. Т. о., если запас капитала меньше уровня по Золотому правилу МРК > d, потребление растет. Если запас капитала больше уровня по Золотому пра­вилу МРК < d – потребление падает. Потребление достигает максимума, когда МРК = d.

Усложним задачу. До сих пор, мы предполагали, что можно просто вы­брать устойчивое состояние с наиболее высоким уровнем потребления в соот­ветствии с Золотым правилом. Теперь посмотрим, что происходит в экономике, если происходит переход от одного устойчивого состояния к другому.

Случай 1. Экономика начинает развиваться с запасом капитала большим, чем по Золотому правилу.

В этом случае, необходимо проводить политику, направленную на сни­жение нормы сбережений, чтобы уменьшить устойчивый уровень запаса капи­тала. На рис. 3.7 показано, что происходит с производством, потреблением и инвестициями. Уменьшение нормы сбережения в момент t₀ вызывает немед­ленный рост потребления и соответствующее снижение инвестиций. По мере уменьшения капиталовооруженности выпуск, потребление и инвестиции одно­временно уменьшаются. Но, так как исходный запас капитала был слишком вы­сок, потребление в новом устойчивом состоянии выше по сравнению с началь­ным состоянием.

Рис. 3.7 - Уменьшение нормы сбережения при начальной

капиталовооруженности большей, чем по Золотому правилу

 

Случай 2. Экономика начинает развиваться с запасом капитала меньшим, чем по Золотому правилу.

В этом случае необходимо увеличивать норму сбережения, чтобы дос­тигнуть точки, соответствующей Золотому правилу. На рис. 3.8 показано, что при этом произойдет. Увеличение нормы сбережения в момент t₀ вызовет не­медленное падение потребления и увеличение инвестиций. Рост инвестиций приведет к росту капиталовооруженности. В свою очередь, рост капиталово­оруженности приведет к росту потребления и инвестиций и к достижению но­

вого устойчивого уровня.

Рис. 3.8 - Увеличение нормы сбережений при начальной

капиталовооруженности меньшей, чем по Золотому правилу

 

Когда начальная капиталовооруженность выше, чем по Золотому пра­вилу, достижение устойчивого состояния с максимумом потребления сопрово­ждается более высоким уровнем потребления в течение всего времени пере­хода.

Когда начальная капиталовооруженность ниже, чем по Золотому пра­вилу, достижение устойчивого состояния с максимумом потребления требует немедленного снижения потребления в настоящем для того, чтобы повысить его в будущем.

 

3.3 Рост населения

Базовая модель Солоу показывает, что само по себе накопление капитала не может объяснить непрерывный экономический рост. Высокий уровень сбе­режений временно приводит к увеличению темпов роста, но, в конце концов, экономика приближается к устойчивому состоянию, при котором запасы капи­тала и объем производства постоянны.

Чтобы объяснить непрерывный экономический рост, необходимо расши­рить модель Солоу за счет включения в нее двух других источников экономи­ческого роста: рост населения и технологический прогресс. Предположим, что население и рабочая сила растут с постоянным темпом n.

Если n = 0,01, это значит, что ежегодно население увеличивается на 1%.

Чтобы понять, как рост населения влияет на устойчивое состояние, необ­ходимо понять, как рост населения влияет на капиталовооруженность. До этого мы считали, что Dk = i – dk (инвестиции увеличивают капиталовооруженность, а выбытие уменьшает). Очевидно, что рост населения также будет уменьшать капиталовооруженность, так как капитал будет теперь распределяться на боль­шее количество рабочих. Приблизительно мы можем записать:

 

Dk = i – dk – nk

 

Перепишем это равенство, заменив i на sf(k):

 

Dk = sf(k) – (d + n)k

 

Теперь видно, что рост населения, также как и выбытие капитала, умень­шает капиталовооруженность. Чтобы запас капитала на одного работника не менялся, необходимо, чтобы i = (d + n)k или sf(k) = (d + n)k.

Величина (d + n)k является критической величиной инвестиций – это инве­стиции, необходимые для поддержания запаса капитала, приходящегося на од­ного работника на постоянном уровне, и включает инвестиции, необходимые для возмещения выбытия капитала dk и инвестиции, необходимые для обеспе­чения капиталом новых работников nk.

Мы знаем, что экономика находится в устойчивом состоянии, если капи­таловооруженность k не изменяется. Воспользуемся рис. 3.4, чтобы на его ос­нове построить график устойчивого уровня капиталовооруженности с учетом роста населения.

Рис. 3.9 - Устойчивый уровень капиталовооруженности с учетом роста

населения

 

В устойчивом состоянии Dk = 0 и i*= dk*+ nk*.

 

Последствия роста населения:

1. В устойчивом состоянии экономики при росте населения капитал и вы­пуск на одного работника остаются постоянными, но так как количество работ­ников растет с темпом n, капитал и объем производства тоже растут с темпом n. Поэтому рост населения может объяснить непрерывный рост валового вы­пуска продукции.

2. На рис. 3.10 показано влияние увеличения темпов роста населения на устойчивый уровень капиталовооруженности. Увеличение темпов роста насе­ления с n₁ до n₂ уменьшает уровень устойчивой капиталовооруженности с k₁ до k₂, но в результате этого уменьшается и производительность у, так как y*= = f(k*). Таким образом, модель Солоу показывает, что при прочих равных условиях страны с более высоким темпом роста населения будут иметь более низкий ВНП на душу населения.

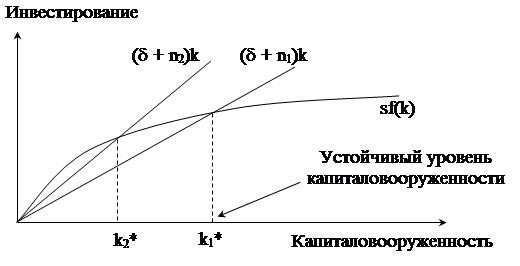Рис. 3.10 - Влияние увеличения темпов роста населения на устойчивый

уровень капиталоворуженности

 

3. Рост населения влияет на уровень накопления капитала по Золо­тому правилу. Вспомним, что потребление на одного работника равно: c = y – i. Так как устойчивый объем производства: y*= f(k*), i*= (d + n)k*,

 

c*= f(k*) – (d + n)k*

 

Мы знаем, что уровень k*, который максимизирует потребление, таков, что

 

MPK = d + n, или МРК – d = n

 

Таким образом, в устойчивом состоянии по Золотому правилу предель­ный продукт капитала минус норма выбытия равен темпу прироста населения.