1 Котеленец Н.Ф., Кузнецов Н.Л. Испытания и надежность электрических машин: Учебное пособие для вузов по спец. «Электромеханика».-М.: Высш. шк., 1988.-232 с., ил.
2 Cборник задач по теории надежности /А.Н. Половко, И.М. Маликов.-М: Сов. Радио, 1972.-408 с., ил.
3 Певзнер Л.Д. Надежность горного электрооборудования и технических средств шахтной автоматики. – М.: Недра, 1983. – 198 с., ил.
Приложение А
Методические указания к решению задачи №1
Так как испытуемые электрические аппараты относятся к классу неремонтируемых изделий, то критериями надежности будут Р(t), а=f(t), λ=f(t), Tср. Вероятность безотказной работы ρ(t) можно вычислять по формуле:
(ПА.1)
где N0 – число изделий в начале испытания;
n(t) – число отказавших изделий за время t или 
.
Частота отказов 
согласно определению определяется по формуле:
, (ПА.2)
где n(∆t) – число отказавших изделий в интервале времени от 
до 
.
Интенсивность отказов 
согласно определения определяется по формуле:
, (ПА.3)
где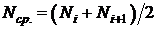 
- среднее число изделий, исправно работающих в интервале времени ∆t;
- число изделий, исправно работающих в начале интервала времени ∆t;
- число изделий, исправно работающих в конце интервала времени ∆t.
Результаты расчетов 
целесообразно сводить в таблицу.
Средняя наработка до первого отказа может определяться по формуле:
, (ПА.4)
В выражении (ПА. 4) 
и m находятся по следующим формулам:
; (ПА.5)
, (ПА.6)
где 
- время начала і- го интервала;
- время конца і- го интервала;
- время, в течение которого вышли из строя все элементы;
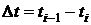- интервал времени.
Зависимость и целесообразно строить в одной координатной системе.
Приложение Б
Методические рекомендации к решению задачи №2
Структурной надежностью системы называется результирующая надежность при заданной структуре и известных значениях надежности всех входящих в нее блоков или элементов.
Расчет надежности при последовательном (основном) соединении элементов.
Когда отказ технического изделия наступает при отказе одного из его узлов, то такое изделие имеет последовательное соединение элементов. Например, электрическая машина практически всегда представляется в виде последовательного соединения узлов.
Если надежность отдельных узлов (элементов) Р1, Р2, …. Рn не зависит друг от друга, то надежность системы, состоящей из N узлов, определяется по формуле:
(ПБ. 1)
Расчет надежности при параллельном соединении элементов (резервирование).
Для повышения надежности часто используется резервирование или дублирование. Например, применяется параллельная работа трансформаторов и синхронных генераторов в энергосистемах, в электронных системах часто используется параллельное включение диодов и т.д. Если в структурной схеме имеется М параллельных ветвей, то результирующая для них вероятность безотказной работы определяется по формуле:
(ПБ. 2)
Расчет надежности при параллельно - последовательном (смешанном) соединении элементов.
Методику расчета надежности рассмотрим на двух наиболее характерных случаях параллельно-последовательных соединений.
В первом случае (его называют общим резервированием с постоянно включенным резервом и целой кратностью) система состоит из M параллельных цепочек по N блоков в каждой (см. рис. ПБ. 1). 
N
|
M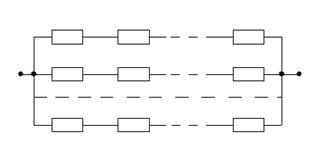 
Рисунок ПБ. 1 – Последовательно-параллельное соединение блоков.
Результирующая вероятность безотказной работы всей системы определяется по формуле:
(ПБ.3)
Во втором случае (его также называют раздельным резервированием с постоянно включенным резервом и целой кратностью) система состоит из последовательно соединенных N групп, состоящих из М параллельно включенных блоков (см. рис. ПБ. 2)
N
|
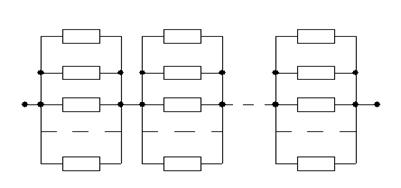
Рисунок ПБ. 2 – Параллельно – последовательное соединение блоков
Результирующая вероятность безотказной работы всей системы определяется по формуле:
, (ПБ.4)
 |  | ||
Пример. Дана структурная схема блока пускорегулирующей аппаратуры (см. рис. ПБ. 3) с известными вероятностями безотказной работы входящих в нее элементов, указанными на рисунке. Требуется найти вероятность безотказной работы всей системы в целом.
 |
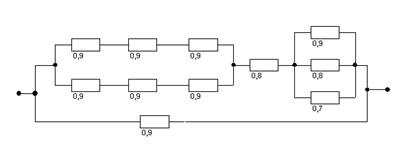
Рисунок ПБ. 3 – Структурная схема
Решение. Представленная система состоит из двух (цепи АВС и Д) параллельных цепей различной надежности. Разберем цепочку АВС, которая состоит из трех блоков. На основании формулы (ПБ.3) определим надежность блока А:
Блок В нерезервируемый и имеет надежность РВ=0,8.
Надежность работы блока С определяется по формуле (ПБ.2):
Вероятность цепочки АВС будет равно:
Результирующая вероятность безотказной работы всей резервируем ой системы будет:
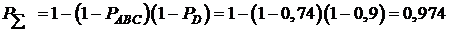
Ответ: 
Приложение В