| Элемент передачи | Марка материала | Dпред | Термооб- работка | НВ | σв | σТ | σ-1 | [σ]F | [σ]н |
| Sпред | Н/мм 2 | ||||||||
| Шестерня | Сталь 40Х | Улучшение | |||||||
| Колесо | 154,5 |
РАСЧЁТ ЗАКРЫТОЙ ПЕРЕДАЧИ.
ПРОЕКТНЫЙ РАСЧЁТ
4.1. Определяем главный параметр – межосевое расстояние аw,мм:
аw >Kа´(u+1)´ 
´KНβ =
= 49,5´(5 + 1)´ 
´1 = 214,08 мм
где: Kа= 49,5 – вспомогательный коэффициент;
KНβ = 1 – коэффициент неравномерности нагрузки по длине зуба;
= 0,3 – коэффициент ширины венц 
а.
полученное значение межосевого расстояния округляем до ближайшего числа по табл. 13.15. и принимаем:
аw = 220 мм.
4.2. Определяем модуль зацепления т, мм:
т > 
мм.
где: 
= 6,8 – вспомогательный коэффициент;
- делительный диаметр колеса, мм:
мм
- ширина венца колеса, мм.
мм.
Полученное значение округляем до стандартного в большую сторону.
т = 1,5 мм.
4.3. Определяем суммарное число зубьев шестерни и колеса:
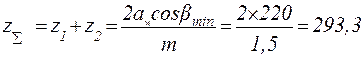
4.4. Определяем число зубьев шестерни:
Округляем до целого числа и принимаем 
=49
4.5. Определяем число зубьев колеса:
= 
- 
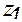=293-49 =244
4.6. Определяем фактическое передаточное число uф и проверяем его отклонение ∆ uф от заданного и:
uф= 
; ∆u = 
´100% < 3,36%
uф = 4,9; ∆u = 2 <3,36%
4.7. Определяем фактическое значение межосевого расстояния аw,мм:
аw =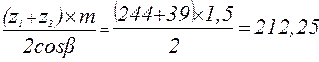 
мм.
4.8. Определяем фактические основные геометрические размеры передачи, мм.
а) Основные размеры шестерни:
делительный диаметр
d1 = тz1 /cosβ = 1,5´49/1 =73,5 мм.
диаметр вершин зубьев
da1 = d1 + 2т = 73,5 +2´1,5 = 76,5 мм.
диаметр впадин зубьев
df1 = d1 – 2,4т = 73,5 – 2,4´1,5 = 69,9 мм.
ширина венца
b1 = b2 + (2…4) = 66 + (2…4) = 68…70 мм.
по таб. 13.15. в полученный интервал входит значение b1 = 70 мм.
|
|
б) Основные размеры колеса:
делительный диаметр:
d2 = тz2 /cosβ = 1,5´244/1 = 366 мм.
диаметр вершин зубьев:
da2 = d2 + 2т = 366 +2´1,5 = 369 мм.
диаметр впадин зубьев:
df2 = d2 – 2,4т = 366 – 2,4´1,5 = 362,4 мм.
ширина венца:
мм.
по таб. 13.15. в полученный интервал входит значение b2 = 66 мм.
ПРОВЕРОЧНЫЙ РАСЧЁТ
4.9. Проверяем межосевое расстояние аw, мм:
аw = (d1 + d2 )/2 = (76,5+366)/2 = 220 мм.
4.10. Проверяем контактные напряжения 
, Н/мм2:
,
где: 
К = 436 – вспомогательный коэффициент
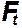- окружная сила в зацеплении, Н;
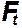= 2Т2´10 3 /d2 = 2´319´1000/366 = 1743,16 Н.
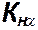=1 – коэффициент учитывающий распределение нагрузки между зубьями в зависимости от окружной скорости 
колес и степени точности передачи
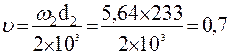м/с.
= 1,05 – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени передачи (таб. 4.3.).
Н/мм2
464,73 < 499
условие прочности выполняется т.к. недогрузка 3,5% не превышает допустимой 10%.
4.11. Проверяем напряжение изгиба зубьев шестерни 
и колеса 
, Н/мм 2:
= 
,
= 
,
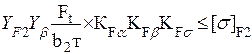где 
=1 – коэффициент учитывающий распределение нагрузки между зубьями;
=1 – коэффициент неравномерности нагрузки по длине зуба для прирабатывающихся колес.
=1,13 – коэффициент динамической нагрузки, зависящий от окружной скорости колёс и степени передачи (таб. 4.3.).
и 
- коэффициенты формы зуба шестерни и колеса
Определяется в зависимости от числа зубьев z1 и z2 :
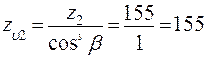
= 3,65 = 3,63
=1 – коэффициент учитывающий наклон зуба:
= 
,
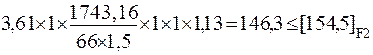условие прочности выполняется < 
, недогрузка 52%.
= 
,
Условие прочности выполняется < 
, недогрузка 56%.
Таблица 4