Одним из центральных звеньев рыночных структур являются коммерческие банки, поэтому развитие их деятельности – необходимое условие функционирования рыночной экономики.
Коммерческие банки принято относить к категории финансовых посредников. Это многофункциональные организации, осуществляющие свою деятельность в различных секторах рынка ссудного капитала: они привлекают капиталы, свободные денежные средства, высвобождающиеся в процессе хозяйственной деятельности, сбережения населения и предоставляют их во временное пользование различным заемщикам, нуждающемся в дополнительном капитале. Таким образом, банки выполняют важную функцию, осуществляя межотраслевое и межрегиональное перераспределение денежных средств.
Операции коммерческих банков делятся на пассивные и активные. К пассивным операциям относятся операции, связанные с формированием ресурсов банка (формирование собственных средств, привлечение средств во вклады и депозиты, выпуск собственных ценных бумаг), к активным – операции, связанные с размещением ресурсов (кредитование, вложение в ценные бумаги и т.д.).
Рассмотрим основные виды расчетов, применяемых при анализе пассивных и активных операций банка.
Основную часть своих потребностей в денежных ресурсах для осуществления активных операций банки покрывают за счет привлеченных средств. К таким средствам в первую очередь относятся депозиты, вклады и средства от продажи собственных ценных бумаг (облигаций, векселей, депозитных и сберегательных сертификатов).
Плата за привлеченные ресурсы банков состоит в выплате процентов за их использование.
При расчете платы за привлеченные ресурсы банки используют две основные методики – наращение по простым и сложным процентным ставкам.
|
|
Для записи формулы наращения простых процентов примем обозначения:
I – сумма начисленных процентов, руб.;
P– первоначальная сумма долга (депозита, кредита, номинал ценной бумаги), руб.;
S – наращенная сумма, то есть сумма в конце срока (P+I), руб.;
i – годовая ставка наращения, %;
n – срок наращения (срок вклада. Депозита, кредита, ценной бумаги), годах.
Если срок измеряется в годах, то каждый год приносит проценты в сумме 
. Следовательно, начисленные за весь срок проценты составят
(1)
Наращенная сумма, таким образом, находится как
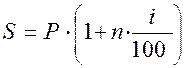(2)
Пример 1. Вкладчик поместил в банк вклад величиною в 15 тыс. руб. под 8% годовых, сроком на два года. Определите, какую сумму денег получит вкладчик по истечении срока вклада.
| Дано: P – 15 тыс.руб. i – 8% годовых n- 2 года | Решение:
Используем формулу 7.
 тыс. руб.
I = 17400-15000 = 2400 тыс.руб.
|
| S -?, I -? | Ответ: S= 17400 тыс.руб., I = 2400 тыс.руб. |
Если же срок банковской операции не равен целому числу лет, то срок n можно выразить в виде дроби n=t/K, где t – число дней, K – расчетное количество дней в году.
Пример 2. Депозитный вклад величиной 1000 руб. помещен в банк на 120 дней под 6% годовых. Определите, какой доход получит вкладчик.
| Дано: P – 1000руб. i – 6% годовых t – 120 дней K – 365 дней | Решение:
Используем формулу 6.
 руб.
|
| I -? | Ответ: 19,7 руб. |
В банковской практике иногда применяются плавающие процентные ставки. В таком случае наращенная на конец срока сумма определяется следующим образом:
(3)
где, it – ставка простых процентов в периоде t, %;
|
|
nt – продолжительность периода с постоянной ставкой i, дни или года.
Пример 3. Банк предлагает следующую схему начисления дохода по вкладу:
- базовая ставка 5% годовых;
- надбавка к базовой ставке за первый месяц 1%, за второй месяц 2%, за третий месяц 3%.
Определите какой доход получит вкладчик, если поместит 20 000 руб. во вклад сроком на 3 месяца.
| Дано: P – 20 000 руб. i – 5% годовых i1 – 6% годовых i2 – 7%годовых i3 – 8%годовых t1,2,3 – 30 дней K – 365 дней | Решение:
Используем формулу 8.
 руб.
I = 20 350 руб. – 20 000 руб. = 350 руб.
|
| I -?, S -? | Ответ: I = 350 руб., S =2350 руб. |
Иногда начисление процентов производится на изменяющиеся суммы во времени (счет, с которого производятся списания и на который производятся зачисления).
Расчет суммы процентов, в данном случае производится по формуле:
(4)
где, Rj – остаток средств в момент j после очередного поступления или списания, руб.;
tj – срок в днях между последовательными изменениями остатков на счете, дни.
Величину 
называют процентным числителем, а 
- процентным делителем.
Пример 4. Движение средств на счете характеризуется следующими данными: 05.02 поступило 12 млн. руб., 10.07 снято 4 млн. руб. и 20.10 поступило 8 млн. руб. Найти сумму на счете на конец года. Процентная ставка 18% годовых.
Решение:
1)процентный делитель составит 365:18 = 20,27778.
2) расчет суммы процентных чисел приведен в следующей таблице.
| Дата | Движение средств | Остаток (Rj) | Срок (tj) | Процентное число |
| 05.02 | 18,6 | |||
| 10.02 | -4 | 8,16 | ||
| 20.10 | 11,52 | |||
| 31.12 | - | - | - | |
| Итого | 38,28 |
Ответ: Сумма процентов за весь срок равна 
млн. руб.
|
|
Помимо расчета процентов по простой процентной ставке коммерческие банки часто прибегают к использованию сложной процентной ставки. То есть происходит капитализация суммы дохода за определенный период, а начисление процентов в следующем периоде производится на увеличенную базу.
Для записи формулы наращения примем те же обозначения, что и для записи формулы простых процентов.
Очевидно, что в конце первого периода проценты равны величине P·i, а наращенная сумма составит 
. К концу второго периода она достигнет величины 
и т.д. В конце n-го периода сумма будет равна
(5)
Проценты за этот период составят
(6)
Пример 5. Вкладчик – физическое лицо – заключил с банком договор о сберегательном вкладе сроком на три года на сумме 50 000 руб. под 12% годовых. По условиям договора банк производит начисление процентов ежегодно и капитализирует их. Определите сумму процентов, которую получит вкладчик по условиям договора.
| Дано: P – 50000руб. i – 12% годовых n – 3 года | Решение:
Используем формулу 11.
 = 20246 руб.
|
| I -? | Ответ: I = 20246 руб. |
Данный метод расчета используется в том случае, когда период капитализации равен году. Если же начисление и капитализация процентов происходят определенное количество раз в течение одного года, то формула для расчета имеет следующий вид
(7)
где, N –количество периодов начисления процентов (месяцев, кварталов и т.п.);
in – процентная ставка за один период начисления (если проценты начисляются ежемесячно, то in = i: 12, сели поквартально, то in = i: 4 и т.д.)
Пример 6. Какой величины достигнет долг, равный 15500 руб. через 5 месяцев при росте по сложной ставке 15,5% годовых.
| Дано: P – 15500руб. i – 15,5% годовых in – 1,291% N – 5 мес. | Решение:
Используем формулу 11.
 = 1026,7 руб.
|
| I -? | Ответ: I = 1026,7 руб. |
Как было отмечено выше, коммерческие банки, аккумулируя свободные денежные ресурсы, размещают их в активные операции. К активным операциям банков относят кассовые, кредитные и инвестиционные, а так же вложения в основные средства.
Основную роль в деятельности банков играют кредитные операции. Ставка, по которой выдаются кредиты, превышает ставку, по которой принимаются депозиты, на величину процентной маржи, являющейся источником прибыли банка.
При расчете платы за предоставленный кредит банки используют простые процентные ставки, поскольку использование сложных ставок будет увеличивать сумму долга, а это противоречит кредитному договору (в котором сумма долга ссудозаемщика фиксируется).
Пример 7. Коммерческий банк заключил с СПК «Красный луч» кредитный договор на сумму 250 000 руб. сроком 6 месяцев. Процентная ставка была установлена на уровне 18% годовых. Требуется определить, какой доход получит банк от данной сделки.
| Дано: P – 250 тыс.руб. i – 18% годовых n – 0,5 года | Решение:
Используем формулу 6.
 22500руб.
|
| I -? | Ответ: 22500 руб. |
Коммерческие банки занимаются кредитованием не только юридических, но и физических лиц. Однако методика расчета платежей в потребительском кредите несколько иная.
В потребительском кредите проценты, как правило, начисляются на всю сумму кредита и присоединяются к основному долгу уже в момент открытия кредита. Погашение долга с процентами производится частями, обычно равными суммами на протяжении всего срока кредита. Из сказанного следует, что наращенная сумма долга рассчитывается по формуле 7, а величина погасительного платежа составит
(8)
где, n – срок кредита в годах;
N – число платежей в году.
Пример 8. Кредит для покупки товара на сумму 100 тыс. руб. открыт на 3 года, расчет процентов производится по ставке 15% годовых. Выплаты по кредиту – в конце каждого месяца. Определите сумму наращенного долга по ссуде и размер погасительного платежа.
| Дано: P – 100 тыс.руб. i – 15% годовых n – 3 года N -36 | Решение:
Используем формулу 7 и рассчитаем сумму наращенного долга.
 = 45000 руб.
Ежемесячные погасительные платежи рассчитаем по формуле 13
 = 1250 руб.
|
| S -?, R -? | Ответ: S - 45000руб., R - 1250 руб. |
В банковской практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую нужно уплатить через некоторое время n, необходимо определить сумму P. Такая ситуация может возникнуть при выдаче так называемой дисконтированной ссуды, когда проценты по кредиту удерживаются вперед, то есть непосредственно при выдаче ссуды.
В этих случаях говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты – дисконтом. Необходимость дисконтирования возникает, например, при покупке краткосрочных обязательств, оплата которых должником произойдет в будущем.
В зависимости от вида процентной ставки применяют два метода дисконтирования – математическое дисконтирование и банковский (коммерческий) учет. В первом случае применяется ставка наращения, во втором – учетная ставка.
Математическое дисконтирование представляет собой решение задачи, обратной наращению первоначальной суммы. Задача, в этом случае формулируется так: какую первоначальную сумму нужно предоставить в долг, чтобы получить в конце срока сумму S, при условии, что на долг начисляются проценты по ставке i? Решив (3) относительно P, находим
(9)
Пример 9. Через 180 дней после подписания договора должник уплатит 310 тыс.руб. Кредит выдан банком под 16% годовых. Какова первоначальная сумма долга, при условии, что временная база равна 365 дням.
| Дано: S – 310 тыс.руб. i – 16% годовых t – 180 дней K -365 дней | Решение:
Используем формулу 14
 = 287328,62 руб.
|
| P -? | Ответ: P - 287328,62 руб. |
Банковский учет отличается от математического дисконтирования. Суть операции заключается в следующем. Банк или другая финансовая организация до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной в этом обязательстве, то есть покупает его с дисконтом. Получив при наступлении срока векселя деньги, банк реализует процентный доход в виде дисконта. В свою очередь владелец векселя с помощью его учета имеет возможность получить деньги хотя и не в полном объеме, однако ранее указанного на нем срока.
При учете векселя применяется банковский или коммерческий учет. Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d. Следовательно
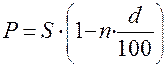(10)
где, n – срок от момента учета до даты погашения, года (если срок выразить в днях, то получим отношение 
, где t – число дней, K – расчетное количество дней в году).
Иногда при разработке финансовых контрактов или их анализе и сравнении возникает необходимость в решении ряда вторичных задач – определении срока (кредита, депозита или эмитируемого долгового обязательства) и размера процентной ставки при прочих заданных условиях.
Необходимые для расчета продолжительности операции в годах и днях формулы получим, решив (3) и (10) относительно n.
Срок в годах:
(11)
Срок в днях (напомним, что , где t – число дней, K – расчетное количество дней в году):
(12)
Необходимость в расчете процентной ставки возникает при определении финансовой эффективности операции и при сравнении контрактов по их доходности, когда процентные ставки в явном виде не указаны. Решив выражения (3) и (10) относительно i или d, получим искомые формулы.
(13)
(14)
Список литературы
Основная
1. Банковское дело: организация деятельности центрального банка и коммерческого банка, небанковских организаций: учебник / А.А. Казимагомедов. - М.: ИНФРА-М, 2018. - 502 с. + Доп. материалы [Электронный ресурс; Режим доступа: https://www.znanium.com]. — (Высшее образование: Бакалавриат). — www.dx.doi.org/10.12737/25095.
2. Организация деятельности коммерческого банка: Учебник / Маркова О.М. - М.: ИД ФОРУМ, НИЦ ИНФРА-М, 2016. - 496 с.: 60x90 1/16. - (Профессиональное образование) (Переплёт) ISBN 978-5-8199-0638-5
Дополнительная
1. Банковское дело: Учебник / Под ред. О.И. Лаврушина; Финансовый университет при Правительстве РФ. - 11-е изд., стер. - М.: Кнорус, 2014.
2. Вешкин Ю. Г. Экономический анализ деятельности коммерческого банка: Учебное пособие. - 2-e изд., перераб. и доп. - М.: Магистр: НИЦ ИНФРА-М, 2014. (ЭБС znanium.com)
3. Ефимова О.В. Финансовый анализ: современный инструментарий для принятия экономических решений: Учебник. - 2-е изд., стер. - М.: Омега-Л, 2010.
4. Куницына Н. Н. Бизнес-планирование в коммерческом банке: Учебное пособие / Н.Н. Куницына, А.В. Малеева, Л.И. Ушвицкий. - М.: Магистр: НИЦ ИНФРА-М, 2014. (ЭБС znanium.com)
5. Маевская Е. Б Стратегический анализ и бюджетирование денежных потоков коммерческих организаций: Монография / Е.Б. Маевская. - М.: НИЦ ИНФРА-М, 2014. (ЭБС znanium.com)
6. Поморина М.А. Финансовое управление в коммерческом банке: учебное пособие. – М.: КноРус, 2013 (ЭБС znanium.com)
7. Тысячникова Н.А., Юденков Ю.Н. Стратегическое планирование в коммерческих банках: концепция, организация, методология. - М.: КноРус, 2013. (ЭБС Book.ru 2013)
Периодические издания
1. Журнал «Деньги и кредит».
2. Журнал «Банковское дело».
6. Перечень ресурсов информационно-коммуникационной сети «Интернет, необходимых для освоения дисциплины:
Сайт Центрального Банка России. — https://www.cbr.ru
При возникновении вопросов в период самостоятельной подготовки в течение семестра обращаться за консультацией к ведущему занятия преподавателю доценту кафедры «Философия, история, право и межкультурная коммуникация» Екатерина Александровне Кузнецовой по адресу:
EAKuznetcova@fa.ru или e.a.kuznetsova@list.ru.