Комплексные числа и многочлены
Комплексные числа в алгебраической форме
Определение 1. Комплексным числом 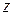 называется выражение
называется выражение
 , (1)
, (1)
где  и
и 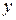 – действительные числа,
– действительные числа, 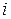 – так называемая мнимая единица, определяемая равенством
– так называемая мнимая единица, определяемая равенством
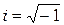 или
или 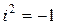 . (2)
. (2)
Действительные числа  и
и 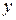 обозначаются
обозначаются 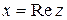 ,
, 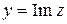 и называются соответственно действительной и мнимой частями комплексного числа
и называются соответственно действительной и мнимой частями комплексного числа 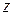 . Если
. Если 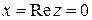 , то число
, то число 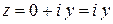 называется чисто мнимым, если
называется чисто мнимым, если 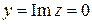 , то число
, то число  является действительным. Таким образом, множество действительных чисел R есть подмножество множества комплексных чисел C.
является действительным. Таким образом, множество действительных чисел R есть подмножество множества комплексных чисел C.
Комплексное число  называется сопряжённым комплексному числу
называется сопряжённым комплексному числу  . Сопряжённые комплексные числа отличаются только знаком мнимой части:
. Сопряжённые комплексные числа отличаются только знаком мнимой части: 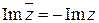 .
.
Т.к. 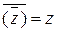 , то числа
, то числа 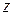 и
и 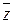 являются взаимно сопряжёнными.
являются взаимно сопряжёнными.
Пример 1.  ,
,  ,
, 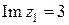 ,
, 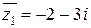 ;
;
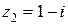 ,
, 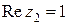 ,
, 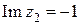 ,
, 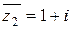 ;
;
 ,
, 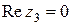 ,
,  ,
,  ;
;
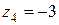 ,
,  ,
, 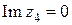 ,
,  .
.
Определение 2. Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части.
Комплексное число 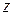 равно нулю тогда и только тогда, когда
равно нулю тогда и только тогда, когда 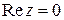 и
и  .
.
Запись комплексного числа в виде (1) называется алгебраической формой записи.
Сложение, вычитание, умножение и деление комплексных чисел в алгебраической форме выполняются по обычным правилам алгебры с учётом соотношения (2). Результат действия также должен быть записан в алгебраической форме.
Пусть 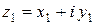 и
и 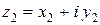 , тогда
, тогда
 , (3)
, (3)
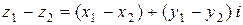 , (4)
, (4)
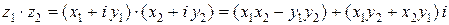 , (5)
, (5)
в частности,
 . (6)
. (6)
Чтобы разделить 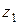 на
на  (при условии, что
(при условии, что 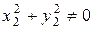 , т.е.
, т.е.  ), делимое и делитель умножаются на число
), делимое и делитель умножаются на число 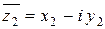 , сопряжённое делителю:
, сопряжённое делителю:
 .
.
Пример 2. Выполним умножение и деление чисел примера 1:
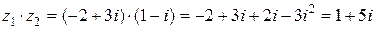 ;
;
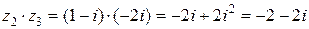 ;
;
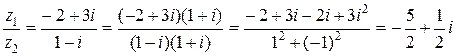 ;
;
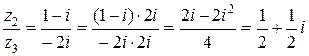 .
.
При выполнении алгебраических действий следует учитывать, что 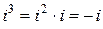 ,
, 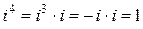 ,
,  и так далее. Вообще, при любом целом n
и так далее. Вообще, при любом целом n
 ,
, 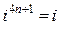 ,
, 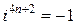 ,
, 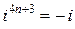 . (7)
. (7)
Геометрическое изображение комплексного числа.
Тригонометрическая и показательная формы записи
Каждое комплексное число  можно изобразить точкой с координатами
можно изобразить точкой с координатами  и
и 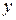 на плоскости с прямоугольной системой координат. Обратно, каждой точке
на плоскости с прямоугольной системой координат. Обратно, каждой точке 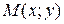 этой плоскости соответствует комплексное число
этой плоскости соответствует комплексное число  . Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексной переменной
. Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексной переменной 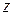 или, кратко, комплексной плоскостью. Ось
или, кратко, комплексной плоскостью. Ось 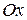 комплексной плоскости называется действительной осью, так как её точкам соответствуют действительные числа. Точкам оси
комплексной плоскости называется действительной осью, так как её точкам соответствуют действительные числа. Точкам оси 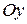 соответствуют чисто мнимые числа, поэтому она называется мнимой осью. Взаимно сопряжённые комплексные числа
соответствуют чисто мнимые числа, поэтому она называется мнимой осью. Взаимно сопряжённые комплексные числа 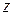 и
и 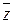 изображаются точками, симметричными относительно действительной оси.
изображаются точками, симметричными относительно действительной оси.
Комплексное число  можно также изображать вектором
можно также изображать вектором 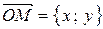 – радиус-вектором точки
– радиус-вектором точки 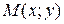 , или любым равным ему вектором.
, или любым равным ему вектором.
Если ввести на комплексной плоскости полярную систему координат 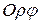 , совместив её с прямоугольной системой
, совместив её с прямоугольной системой 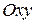 , то
, то 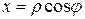 ,
, 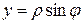 , и число
, и число  представляется в виде
представляется в виде
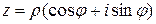 , (8)
, (8)
называемым тригонометрической формой записи комплексного числа 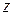 . Величины
. Величины 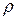 и
и 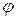 обозначаются
обозначаются 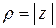 ,
, 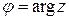 и называются соответственно модулем и аргументом комплексного числа
и называются соответственно модулем и аргументом комплексного числа 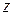 .
.
Модуль числа 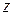 геометрически представляет собой расстояние от начала координат
геометрически представляет собой расстояние от начала координат 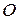 до точки
до точки 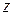 (длину её радиус-вектора):
(длину её радиус-вектора):
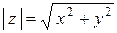 , (9)
, (9)
при этом  . Из соотношений (6) и (9) следует важное свойство:
. Из соотношений (6) и (9) следует важное свойство:
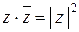 . (10)
. (10)
Аргумент комплексного числа 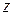 , будучи полярным углом точки
, будучи полярным углом точки 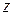 , определяется не однозначно, а с точностью до слагаемого
, определяется не однозначно, а с точностью до слагаемого 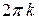 , где
, где 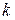 – любое целое число. Чтобы аргумент определялся однозначно, его считают изменяющимся в пределах
– любое целое число. Чтобы аргумент определялся однозначно, его считают изменяющимся в пределах 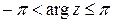 и называют тогда главным значением аргумента комплексного числа
и называют тогда главным значением аргумента комплексного числа 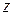 . Находить главное значение аргумента числа
. Находить главное значение аргумента числа  удобно по формуле
удобно по формуле
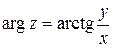 , (11)
, (11)
выбирая из двух возможных значений угла то, которое соответствует расположению точки 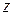 на комплексной плоскости.
на комплексной плоскости.
Точка 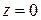 (начало координат) является единственной точкой комплексной плоскости, для которой
(начало координат) является единственной точкой комплексной плоскости, для которой  не определён (в качестве него можно принять любой угол). Модуль числа
не определён (в качестве него можно принять любой угол). Модуль числа 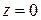 равен нулю.
равен нулю.
Пример 3. Запишем числа  ,
, 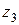 и
и 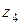 примера 1 в тригонометрической форме.
примера 1 в тригонометрической форме.
Для числа 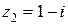 находим
находим 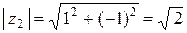 ,
, 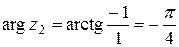 или
или 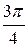 . Так как изображающая число
. Так как изображающая число  точка располагается в четвёртом квадранте комплексной плоскости, то
точка располагается в четвёртом квадранте комплексной плоскости, то 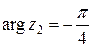 . Окончательно имеем
. Окончательно имеем  .
.
У чисто мнимого числа  модуль
модуль 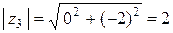 , аргумент
, аргумент 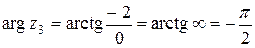 , т.к. точка
, т.к. точка 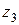 располагается на отрицательной части мнимой оси. Тригонометрическая форма числа
располагается на отрицательной части мнимой оси. Тригонометрическая форма числа 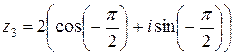 .
.
Число 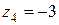 имеет модуль
имеет модуль  , аргумент
, аргумент 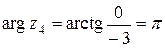 , т.к. точка
, т.к. точка 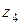 лежит на отрицательной части действительной оси. Получаем, что
лежит на отрицательной части действительной оси. Получаем, что 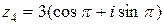 .
.
Из формул (3) и (4) следует, что сложение и вычитание комплексных чисел, изображённых векторами, может производиться по геометрическим правилам сложения и вычитания векторов. При этом модуль разности двух комплексных чисел 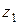 и
и  равен расстоянию
равен расстоянию  между точками
между точками 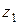 и
и  комплексной плоскости. Это означает, что уравнение окружности радиуса
комплексной плоскости. Это означает, что уравнение окружности радиуса  с центром в точке
с центром в точке 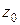 записывается в виде
записывается в виде  .
.
Если по правилам алгебраических действий умножить (разделить) комплексное число 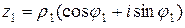 на число
на число 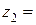
 и использовать формулы косинуса и синуса суммы (разности) двух углов, то получим правило умножения (деления) комплексных чисел в тригонометрической форме, заключающееся в том, что при умножении (делении) комплексных чисел их модули перемножаются (делятся), а аргументы складываются (вычитаются):
и использовать формулы косинуса и синуса суммы (разности) двух углов, то получим правило умножения (деления) комплексных чисел в тригонометрической форме, заключающееся в том, что при умножении (делении) комплексных чисел их модули перемножаются (делятся), а аргументы складываются (вычитаются):
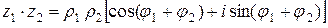 , (12)
, (12)
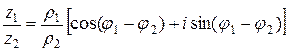 . (13)
. (13)
Пример 4. Найдём произведение и частное чисел  и
и 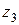 , заданных в тригонометрической форме (пример 3). Имеем
, заданных в тригонометрической форме (пример 3). Имеем
 =
=
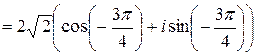 ,
,
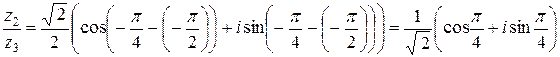 .
.
Следствием правила умножения является формула Муавра возведения комплексного числа в целую положительную степень 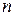 :
:
 . (14)
. (14)
Корнем 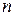 -ой степени из комплексного числа
-ой степени из комплексного числа 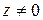 называется комплексное число
называется комплексное число 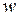 , являющееся решением уравнения
, являющееся решением уравнения  и обозначаемое
и обозначаемое  . Пусть
. Пусть 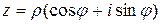 и
и 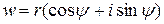 . Так как у равных комплексных чисел модули равны, а аргументы могут отличаться на число, кратное
. Так как у равных комплексных чисел модули равны, а аргументы могут отличаться на число, кратное  , то
, то 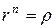 ,
, 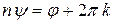 , где
, где 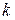 – любое целое число. Отсюда следует формула извлечения корня:
– любое целое число. Отсюда следует формула извлечения корня:
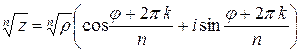 ,
, 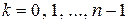 , (15)
, (15)
в которой  – арифметическое значение корня из положительного числа
– арифметическое значение корня из положительного числа 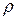 . Значения
. Значения 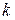 , отличающиеся от приведённых в (15), дают повторяющиеся значения корня. Таким образом, корень
, отличающиеся от приведённых в (15), дают повторяющиеся значения корня. Таким образом, корень 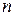 -ой степени из комплексного числа имеет
-ой степени из комплексного числа имеет 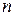 различных значений.
различных значений.
На множестве комплексных чисел имеет место формула Эйлера
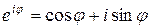 , (16)
, (16)
обосновать которую можно с помощью теории степенных рядов (см.). Применяя (16) к тригонометрической записи комплексного числа (8), получаем показательную форму записи комплексного числа
 , (17)
, (17)
в которой 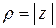 ,
, 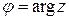 .
.
Пример 5. Для чисел  ,
, 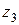 и
и 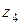 примера 3
примера 3
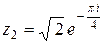 ,
, 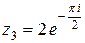 ,
,  .
.