ОДп.02.
Информатика и ИКТ
Автомеханик
УРОК № 11
Группа: АМ-3-20
Дата: 05.11.2020 г.
Преподаватель: Л.Н.Иванова
ТЕМА УРОКА: ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. ДВОИЧНАЯ
АРИФМЕТИКА
Цель урока: расширение знаний о системах счисления, двоичная система счисления. двоичная арифметика.
Давайте вспомним:
· Что называется, системой счисления? (знаковая система, в которой приняты определенные правила записи чисел)
· Что такое алфавит системы счисления? (совокупность цифр, используемых для записи чисел)
· Для чего нужно основание системы счисления? Что оно показывает? (количество цифр в алфавите)
Итак:
Система счисления - это знаковая система, в которой приняты определённые правила записи чисел.
Алфавит системы счисления - совокупность цифр.
Основание системы счисления равно количеству цифр, составляющих её алфавит. Существуют следующие системы счисления:
Десятичная 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двоичная 2 0, 1
Восьмеричная 8 0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А(10), В(11), С(12), D(13), E(14), F(15).
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Двоичной системой счисления называется позиционная система счисления с основанием 2.
Двоичный алфавит: 0 и 1.
Для целых двоичных чисел можно записать:
100112 = 1´24+0´23+0´22+1´21+1´20 = 24 +21 + 20 = 1910
111012 =1´24+1´23+1´22+0´21+1´20 = 24 +23 + 22 +1=2910
ДВОИЧНАЯ АРИФМЕТИКА
Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:
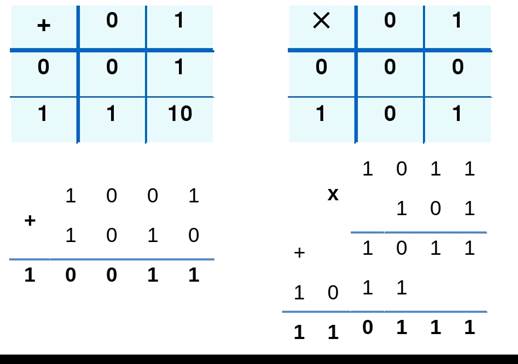
Для того чтобы лучше освоить двоичную систему счисления, необходимо освоить выполнение арифметических действий над двоичными числами.
Все позиционные системы «одинаковы», а именно, во всех них арифметические операции выполняются по одним и тем же правилам:
- справедливы одни и те же законы арифметики: коммуникативный, ассоциативный, дистрибутивный;
- справедливы правила сложения, вычитания, умножения и деления столбиком;
- правила выполнения арифметических операций опираются на таблицы сложения и умножения.
Сложение.
Таблица сложения двоичных чисел проста.
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
1 + 1 + 1 = 11
При сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания.
Пример.

Вычитание.
0 – 0 = 0
0 – 1 = 11
1 – 0 = 1
1 – 1 = 0
Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведённой таблицей вычитания с учетом возможных заёмов из старших разрядов.
Пример.

Умножение.
Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя.
Пример.

Деление.
При делении столбиком приходится в качестве промежуточных результатов выполнять действия умножения и вычитания.
Пример.

Решение задач.
Выполните сложение:
1001001 + 10101 (ответ 1011110);
101101 + 1101101 (ответ 10011010)
11000,11 + 11010,11 (ответ 110011,1)
Выполните вычитание:
10001000 – 1110011 (ответ 10101)
1101100 – 10110110 (ответ – 1001010)
110101,101 – 1001,111 (101011,11)
Выполните умножение:
100001х111,11 (ответ: 11111111,11)
10011х1111,01 (ответ: 100100001,11)
Выполните деление:
1000000 / 1110 (ответ:100)
11101001000/111100 (ответ: 11111)
ДОМАШНЕЕ ЗАДАНИЕ
1. Выполните операцию сложения над двоичными числами:
А) 101010+1101=…
Б) 1010+1010 = …
В) 10101+111 = …
2. Выполните операцию умножения над двоичными числами:
А) 1010х11 = …
Б) 111х101 = …
В) 1010х111 = …
Ответ на домашнее задание
(в виде фотографий или документов Microsoft Word)
прислать на электронный адрес:
larisanikolaevna.epgl@yandex.ru