Выражение (11) представляет собой упрощенный вариант релятивистских преобразований координат, справедливый при нулевых их начальных значениях (для большей наглядности). Нетрудно видеть, что любые соотношения однонаправленных координат и времен
, (12)
представляет собой инвариантную величину, равную скорости света 
, что и наблюдается в реальной природе.
А теперь вновь обратимся к выражению (6). Очевидно, что оно остается справедливым только для одного единственного случая, а именно для плоскости 
, проходящей через центр движущейся системы отсчета 
и перпендикулярной вектору скорости ее движения относительно неподвижной системы отсчета.
Действительно, если рассмотреть прямоугольный треугольник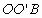 
(рис. 1) с отрезком 
, лежащим в вышеуказанной плоскости, то видно, что только для него последнее слагаемое в выражении (5) обращается в нуль так, что оно превращается в выражение (6). Таким образом, оказывается, что как ковариантность интервала, так и правомочность использования преобразований Лоренца справедливы только для ортогональных компонент преобразуемых величин (традиционная электродинамика этому удовлетворяет).
А теперь детальнее проанализируем формулы преобразования Лоренца:
. (13)
В них не все так просто, как кажется на первый взгляд. И касается это, в первую очередь, соотношения между интервалом времени между двумя какими-то событиями и величиной единицы времени. Очевидно, что, увеличивая единицу времени (при каких-либо преобразованиях координат), мы тем самым сокращаем интервал времени между двумя событиями. И наоборот, сокращая единицу времени, мы тем самым увеличиваем интервал времени. Так что же описывают преобразования (13): изменение интервала времени или единицы времени?
Если во втором соотношении выражения (13) взять 
, то получится выражение
, (14)
которое совпадает с формулами преобразований (11) для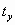 
и 
, т.е. “работает” только в плоскости, перпендикулярной вектору скорости движения подвижной системы отсчета.
Именно так и нужно записывать выражение для изменения единицы времени при переходе к движущейся системе отсчета. Но если преобразуется интервал времени, то соотношение (14) изменится к виду
. (15)
Именно данная формула, как считается в СТО, описывает замедление хода времени в движущейся системе отсчета. Однако если наблюдатель находится в движущейся системе отсчета, то все эти рассуждения носят абсолютно противоположный характер, что является полным абсурдом СТО.
В конечном итоге, если перейти к соответствующим соотношениям единиц (дифференциалов) пространства и времени, то данные преобразования нужно записать в виде:
(16)
Как известно, электромагнитные волны в электродинамике Максвелла поперечны, т.е. их векторы электрической 
и магнитной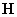 
напряженностей находятся в перпендикулярной к направлению распространения плоскости. Применение преобразований Лоренца к этим компонентам электромагнитного поля давало единственный правильный результат, что и стало триумфом вышеуказанных преобразований. Это подтолкнуло ученых считать и все остальные комбинации правильными.
Между тем, ряд электромагнитных явлений (продольные электромагнитные волны, продольные силы между токовыми элементами, несоблюдение законов сохранения в некоторых задачах традиционной электродинамике и т.п.) уже давно ставят под сомнение всеобщую правильность преобразований Лоренца и полноту уравнений Максвелла. Несоответствие этих преобразований элементарным определениям единиц длины и времени – новое тому доказательство.
Из вышеуказанных рассуждений также вытекает важный вывод о существовании синхронной деформации пространства-времени при переходе от одной инерциальной системы отсчета к другой, а не замедления времени, как это принято в СТО. Данное обстоятельство подтверждается также тем, что вышеуказанные преобразования (11) и (16) не только сохраняют инвариантной скорость света, но и дают правильные результаты для аберрации света и поперечного эффекта Допплера. В то же время продольный эффект Допплера для света должен выражаться такой же формулой, как и соответствующий эффект Допплера для звука при неподвижном относительно воздуха источнике. Это результат различий двух преобразований, касающийся только продольных компонент преобразуемых величин.