Создание стальной балки
Спроектировать стальную балку (рис. 6,а) в 5 вариантах поперечного сечения: круглого, прямоугольного (h/b=2), двутаврового, из швеллеров и уголков, приняв допускаемое напряжение [σ] = 160 МПа. Оценить экономичность всех пяти сечений и начертить их в одном масштабе. Для балки двутаврового профиля построить эпюры нормальных и касательных напряжений, а также исследовать аналитически и графически напряженное состояние в точке К опорного сечения.
Принять: М = 4qa2 кН·м, F = 2qa кН, q=15 кН/м, а = 1,2 м, yк /h= – 0,1
Решение
1. Определение опорных реакций и построение эпюр Qy и Mx.
ΣYi=0
RA - 2qa + q2a = 0
RA =4qa
ΣmA=0
MA - 4qa2 + 2qa3a-q2a2a = 0
MA = 4qa2 + 6qa2 + 4qa2 = 14qa2
Эпюра Qy. Строится по формуле
Q = Q0 ± qz
В данном случае следует взять знак «минус», так как погонная нагрузка направлена вниз. Поперечная сила постоянна на участке АВ (q=0) и изображается наклонной прямой на участке MF (q=const). Вычисляем значения Qy в характерных точках и строим ее эпюру (рис. 6,б)
QA=RA=4qa
QAB=QA=4qa
QBC=QAB – q2a=4qa – 2qa=2qa
QC =QBC – 2qa=2qa – 2qa=0
Эпюра Mx. Строится по формуле
Mx = M0 + Q0Z – 0,5qz2
Изгибающий момент изменяется по квадратичному закону на участке MF (q=const) и по линейному закону – на участке АВ (q=0). Вычисляем значения в характерных точках и строим эпюру (рис. 6,в)
MA = – 14qa2
MAВ = MA + 4qa2 = – 14qa2+ 4qa2 = – 10qa2
MВ = MAВ + 4qa2 = – 10qa2+ 4qa2 = – 6qa2
MВС = MВ + 6qa2 = – 6qa2+ 6qa2 = 0
Расчетный изгибающий момент равен
Mрас = |MA| = 14qa2 = – 14·15·103·1,2 = 302,4 кН·м
Подбор сечений.
Из условий прочности по нормальным напряжениям определяем требуемый момент сопротивления поперечного сечения по кторому подбираем конкретные сечения

 см3
см3
Круг:

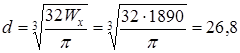 см
см
Принимаем по ГОСТ 6636-86 нормализованное значение d0=270 мм, тогда
 см3
см3
Прямоугольник (h/b=2):

 см
см
Ближайшее меньшее стандартное значение равно b0=140 мм. При этом балка будет работать с перенапряжением, равным
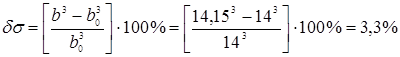
что удовлетворяет требованию, и для которого
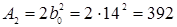 см2
см2
Двутавр. По ГОСТ 8239-89 выбираем двутавр № 55 для которого  =2035 см3, A3=118 см2.
=2035 см3, A3=118 см2.
Три швеллера. По ГОСТ 8240-89 выбираем три швеллера № 36, для которых  =3·601=1803 см3, A4=3·53,4=160,2 см2.
=3·601=1803 см3, A4=3·53,4=160,2 см2.
Неравнобокие уголки. Они находятся подбором, так как в сортаменте не даны значения момента сопротивления. Использую формулу

Сделав несколько попыток, выбираем восемь уголков 250´160´16 для которых
 см3
см3
A5=8·63б6=508,8 см2
Оценка экономичности подобранных сечений
Масса балки определяется как произведение плотности материала на ее объем m=rAl, т.е. расход материала при прочих равных условиях зависит только от площади поперечного сечения А. Сравнивая массы балок
m1: m2: m3: m4: m5 = A1: A2: A3: A4: A5 = 1: 0,68: 0,2: 0,28: 0,89 заключаем, что самым неэкономичным является круглое сечение. При замене круга другими формами (прямоугольник, двутавр, три швеллера, восемь уголков) достигается экономия, равная соответственно 32%, 80%, 72% и 11%.
Исследование напряжений в опорном сечении для балки двутаврового профиля № 55 (рис. 7,а), параметры которой по ГОСТ 8239-89 равны:
h=55 см, b=18 см, d=1,1 см, t=1,65 см, Ix=55962 см4, Sx=1181 см3
Внутренние силовые факторы в опорном сечении А:
QA = 4qa=4·15·1,2 = 72 кН
MA = – 14qa2 = – 14·15·103·1,22 = – 302,4 кН·м
Эпюра σ. Нормальные напряжения в поперечном сечении изменяются по линейному закону
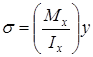
Вычисляем напряжения в крайних точках и строим эпюру σ (рис. 7,б)
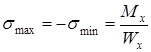
Эпюра τ. Она строится по формуле Журавского

Находим значения τ в 4 характерных точках по высоте сечения (необходимые вычисления представлены в табл. 3) и строим касательные напряжения (рис. 7,в)
Таблица 3 – Вычисления касательные напряжений в характерных точках
| № точек | bi, мм |  , см3 , см3
| 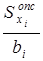
| 
|  , МПа , МПа
| 
|
| 1,1΄ | 
 МПа МПа
| |||||
| 2,2΄ | 0,04 | 0,6 | ||||
| 3,3΄ | 1,1 | 0,7 | 9,3 | |||
| 1,1 | 1073,6 |
Определение главных напряжений в точке К (yк /h= – 0,1):
– напряжение в поперечном сечении
 МПа
МПа
 МПа
МПа
– величины главных напряжений

σ1 = 35,25 МПа
σ3 = – 5,25 МПа
– ориентация главных площадок
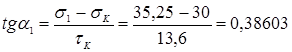
 21º
21º
Экстремальные касательные напряжения равны по величине
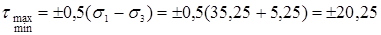 МПа
МПа
и действуют на площадках, равнонаклоненных к осям 1 и 3.
Выбор материала
Согласно схеме нагружения (рис. 9,а), подобрать сечение балки (рис. 10), изготовленной из материала, неодинаково работающего на растяжение и сжатие.
Принять: М = 4qa2 кН·м, F = 2qa кН, q= 15 кН/м, а = 1,2 м,
[σр] = 40 МПа, [σс] = 70 МПа
Решение
1. Определение опорных реакций и построение эпюр Qx и Mx.
ΣmB=0
RA4a - 2qaa - 4qa2- q3a3,5a = 0
RA = 4,125qa
ΣYi=0
RA - 2qa - q3a+ RB = 0
RB =0,875qa
Эпюра Qy. Строится по формуле
Q = Q0 ± qz
В данном случае берем знак «минус», так как погонная нагрузка направлена вниз. Находим значения поперечной силы в характерных точках и строим ее эпюру (рис. 9,б)
QС = 0
QCA = QC –qa= – qa
QA = QCA + RA = – qa + 4,125qa = 3,125qa
QAF = QA – 2qa = 3,125qa – 2qa = 1,125qa
QFD = QAF = 1,125qa
QD = QFD – 2qa = 1,125qa – 2qa = – 0,875qa
QDB = QD = – 0,875qa
QB = QDB + RB = – 0,875qa + 0,875qa = 0
Эпюра Mx. Строится по формуле
Mx = M0 + Q0Z – 0,5qz2
Изгибающий момент изменяется по квадратичному закону на участке CA и AF (q=const) и по линейному закону – на участках FD и DB (q=0). Вычисляем значения в характерных точках и строим эпюру (рис. 9,в)
MС = –4qa2
MA = MС –  qa2 = – 4qa2 – 0,5 = – 4,5qa2
qa2 = – 4qa2 – 0,5 = – 4,5qa2
MF = MA +  qa2 = – 10qa2+ 4qa2 = – 6qa2
qa2 = – 10qa2+ 4qa2 = – 6qa2
MD = MF + 1,125qa2 = – 0,25qa2+ 1,125qa2 = 0,875qa2
MB = MD – 0,875qa2 = 0,875qa2+ 0,875qa2 = 0
Расчетный изгибающий момент равен
Mрас = |MA| = 4,5qa2 = 4,5·15·103·1,22 = 97,2 кН·м
Геометрические характеристики сечения
Положение центра тяжести.
Необходимые вычисления представлены в табл. 4.
Таблица 4 – Положение центра тяжести
| № п/п | υi | Ai | υi Ai |
| 2t | 8t2 | 16t3 | |
| t | – 3t2 | – 3t3 | |
| Σ | 5t2 | 13t3 |

Момент инерции относительно главной центральной оси.
Предварительно определим моменты для элементов сечения относительно собственных центральных осей, а последующие вычисления выполним в табличной форме (табл. 5)
Таблица 5 – Момент инерции
| № эл-в | yi | Ai | 
| yi = υi – υc
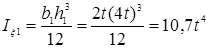

|

| 
| |||
| –0,6t | 8t2 | 10,7t4 | 2,88t4 | |
| –1,6t | –3t2 | –1,5t4 | –7,68t4 | |
| Σ | 9,2t4 | –4,8t4 | ||
| 4,4t4 |
Момент сопротивления


Поскольку материал хуже работает на растяжение, то с точки зрения наиболее эффективного его использования профиль следует расположить так, чтобы более тонкий слой толщиной h2 испытывал растяжение в опасном сечении А. В этом сечении растяжение возникает в верхней части балки, поэтому профиль следует расположить полостью вниз.
Подбор сечения балки.
Находим необходимые размеры:
– из условия прочности на растяжение

 мм
мм
– из условия прочности на сжатие

 мм
мм
Принимаем большее значение t = max { tр, tс} = 113 мм.
В опорном сечение D изгибающий момент меньше расчетного. Поэтому здесь нужно проверить прочность балки на растяжение. Находим
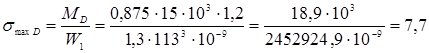 МПа
МПа
Т.к. перенапряжение составляет 15,4%, что недопустимо, принимаем t =200 мм
 МПа
МПа
В этом случае перенапряжение составляет 2,78%, что допустимо, т.к. 2,78% < 5%, следовательно прочность балки при найденных размерах будет обеспечена.
Создание стержня определенной жесткости
Подобрать сечение балки (рис. 11,а), удовлетворяющее условиям прочности и жесткости. Допускаемое напряжение материала определяется исходя из диаграммы растяжения материала (задача 1.3). Исследование перемещения выполнить двумя способами:
– пользуясь методом начальных параметров, определить прогибы и углы поворота сечений балки с координатами z = 0, a, 2a, 3a, 4a, 5a; изобразить изогнутую ось балки и показать на ней найденные перемещения;
– определить прогибы в середине пролета и на концах консолей, а также углы поворота на опорах энергетическим методом.
Принять: q= 15 кН/м, а = 1,2 м, [σ] = 220 МПа, l / [ f ] = 800
Решение
1. Определение опорных реакций и построение эпюр поперечной силы и изгибающего момента.
ΣmB=0
RA4a + 1,5qa2 – q4a2а- 1,5qa·a = 0
RA = 2qa
ΣYi=0
RA - 4qa + 1,5qa + RB = 0
RB =0,5qa
Эпюра Qy. Поперечная сила изменяется на всех участках по линейному и принимает в характерных точках следующие значения (рис. 11,б)
QA=RA=2qa
QAD=QA – qa=2qa – qa=qa
QDB=QAD –q3a=qa – 3qa= – 2qa
QB=QDB + RB = – 2qa + 0,5qa= – 1,5qa
QBC =QB = – 1,5qa
QC=QDC + 1,5qa = – 1,5qa +1,5qa = 0
Эпюра Mx. Изгибающий момент изменяется по квадратичному закону на участке AB (q=const) и по линейному закону – на участке BC (q=0). Вычисляем значения в характерных точках и строим эпюру (рис. 11,в)
MA = 0
MAD = MA +  qa2 = 0+ 1,5qa2 = 1,5qa2
qa2 = 0+ 1,5qa2 = 1,5qa2
MD = MAD + 1,5qa2 = 1,5qa2+ 1,5qa2 = 3qa2
ME = MD +  qa2 = 3qa2+ 0,5qa2 = 3,5qa2
qa2 = 3qa2+ 0,5qa2 = 3,5qa2
MB = ME –  qa2 = 3,5qa2 – 2qa2 = 1,5qa2
qa2 = 3,5qa2 – 2qa2 = 1,5qa2
MC = MB – 1,5qa2 = 1,5qa2 – 1,5qa2 = 0
Расчетный изгибающий момент равен
Mрас = |ME| = 3,5qa2 = 3,5·15·103·1,22 = 75,6 кН·м
Определение перемещений.
Для перемещения упругих перемещений в инженерной практике применяются как аналитические (точные и приближенные), так и графические методы. Из точных аналитических методов следует отметить метод начальных параметров и энергетический метод. К приближенным относят метод конечных разностей (МКР) и метод конечных элементов (МКЭ).
Определим первыми двумя методами.
Метод начальных параметров.
Из граничных условий задачи имеем: νA = 0, νB = 0. Первое дает ν0 = 0, а из второго находим θ0:

откуда

А теперь находим искомые перемещения:
– сечение z=a


– сечение z=2a




– сечение z=3a
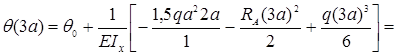



– сечение z=4a



– сечение z=5a
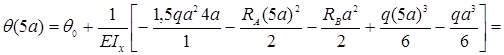



Результаты вычислений сведем в табл. 6 и построим упругую линию балки, показано на рис. 11,а пунктиром.
Таблица 6 – Перемещения и угол поворота в сечение балки
| Перемещения | Сечение z | |||||
| а | 2а | 3а | 4а | 5а | ||
θ´ 
| 
| 
| 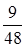
| 
| 
| 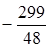
|
ν´ 
| 
| 
| 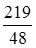
| 
|
Для расчета балки на жесткость необходимо знать максимальный прогиб, который имеет место в сечении, где угол поворота равен нулю. Последний описывает полиномом 3-й степени и в связи с этим нахождение максимального прогиба связано с громоздкими вычислениями. С другой стороны, судя по приведенной выше таблице, он имеет место в интервале (2а, 3а). В силу непрерывности функции прогибов νmax мало отличается от прогиба сечения E. Следовательно, с небольшой погрешность (не превышающей точности инженерных расчетов) можно принять
νmax ≈ νЕ = 
Энергетический метод
Искомые перемещения находятся с помощью интеграла Мора
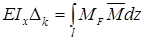
для вычисления которых в простых случаях можно пользоваться правилом Верещагина

а в более сложных случаях – формулой Симпсона
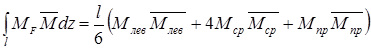
При наличие на данном участке равномерно распределенной погонной нагрузки q величина момента посредине участка находится следующим образом

Величина моментов Млев и Мпр берутся со своими знаками. Знак «плюс» перед вторым слагаемым соответствует погонной нагрузке, направленной вниз, а «минус» – вверх.
Строим эпюры моментов от заданной нагрузки и от единичных воздействий, приложенных к балке в направлении искомых перемещений (рис. 11,г – з).
Определяем моменты по средине участков
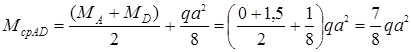



Перемножая соответствующие эпюры, находим искомые перемещения, увеличенные для удобства вычислений в EI раз:










Знак «минус» у перемещения указывает, что оно противоположно направлению соответствующего единичного фактора: единичной силы для прогиба сечения С и единичного момента для угла поворота сечения В, т.е. прогиб νС направлен вверх, а сечение В поворачивается против часовой стрелки. Знак «плюс» у угла поворота θА указывает, что сечение В поворачивается в направлении единичного момента, т.е. по часовой стрелки.
Подбор сечения балки по условиям прочности и жесткости.
Из условия прочности имеем

Отсюда, учитывая что
Mmax = 75,6 кН

находим диаметр сечения балки, удовлетворяющий условию прочности
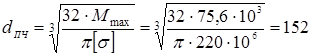 мм
мм
Далее согласно условию жесткости

откуда с учетом

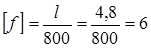 мм
мм
находим искомый диаметр, удовлетворяющий условию жесткости
 мм
мм
Из двух полученных значений принимаем большее, т.е.
d = max {dпч,dж} = dж = 237 мм
После округления до ближайшего стандартного значения по ГОСТ 6636-86 окончательно получим d0 =240 мм.
Найденное таким образом значение диаметра поперечного сечения бруса, обеспечит надежную работу балки, так как удовлетворяет одновременно и условию прочности, и условию жесткости.