Тема: Логарифмические уравнения. Решение задач.
Дата: 23.10.2020 г.
Группа: ПЦ-262
Студенты должны знать: понятия логарифма, логарифмической функции, ее свойства, алгоритм решения логарифмических уравнений, методы их решения.
Студенты должны уметь: решать логарифмические уравнения, применяя различные методы.
Актуализация знаний студентов.
- Определение логарифмического уравнения

- Основные логарифмические тождества

-Свойства логарифмической функции
Свойства функции у = logа x, a > 1.
1. D(f) – множество всех положительных чисел R+.
2. E(f) - множество всех действительных чисел R.
3. Функция является ни четной, ни нечетной
4. При всех значениях а график функции пересекает ось абсцисс в точке х = 1.
5. Промежутки знакопостоянства:
у > 0 при x? (1; +∞)
у < 0 при х? (0; 1).
6. Функция возрастает при x? (0; +∞).
7. Функция непрерывна
Свойства функции у = logаx, 0 < a < 1
1. D (f) – множество всех положительных чисел R+.
2. E (f) - множество всех действительных чисел R.
3. Функция является ни четной, ни нечетной
4. При всех значениях а график функции пересекает ось абсцисс в точке х = 1.
5. Промежутки знакопостоянства:
у > 0 при x? (0; 1)
у < 0 при х? (1; +∞).
6. Функция убывает при
x? (0; +∞).
7. Функция непрерывна.
-Какие уравнения называются логарифмическими?
Уравнение вида Logаf(x) = logаg(x) (или сводящееся к этому виду) называют логарифмическим
- Методы решения логарифмических уравнений:
1. Решение уравнений на основании определения логарифма, например, уравнение logах = в (а > 0, а≠ 1, в>0) имеет решение х = ав.
2. Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их:
если, logаf(х) = logаg(х), то f(х) = g(х), f(х)>0, g(х)>0, а > 0, а≠ 1.
3. Метод введение новой переменной.
4. Метод логарифмирования обеих частей уравнения.
5. Метод приведения логарифмов к одному и тому же основанию.
6. Функционально – графический метод.
-Нужна ли проверка полученных корней при решении логарифмических уравнений? Почему?
Закрепление навыков решения логарифмических уравнений.
Этапы решения уравнения:(проговорить)
а) Найти область допустимых значений (ОДЗ) переменной
б) Решить уравнение, выбрав метод решения
в) Проверить найденные корни непосредственной подстановкой в исходное уравнение или выяснить, удовлетворяют ли они условиям ОДЗ
 2.Решение задач
2.Решение задач
3. log х+1(2x2+1) =2
По определению логарифма имеем: 2х2+1=(х+1)2,
х2-2x=0
x=2 или x=0.
Проверка:
х=0 не может быть корнем данного уравнения, так как основание логарифма х+1≠1.
При х=2 log2+1(2•22+1) =log39=2.
Ответ: 2.
4. log5x=log5(6-x2)
Из равенства логарифмов следует:
x= 6- x2
x2-x-6=0; D=25
x=-3 или x=2.
Проверка:
x=-3 корнем уравнения быть не может, так как логарифмы отрицательных чисел не существуют.
Log5x=log52,
Log5(6-x2) = log5(6-22) =log52.
Ответ: 2.
5. lg2x3- 10lgx + 1=0
Приведём уравнение к квадратному:
Т.к. lg2 x3=(lgx3)2=(3lgx)2= 9lg2x, то
9lg2 x - 10lgx+1=0.
Пусть lg x=y, тогда 9y2- 10y+1=0; D=64
y=1 или y=1/9
lgx=1 или lgx=1/9
x=10 или х=10 1/9.
Проверкой подтверждаем, что оба числа являются корнями.
Ответ: 10; 10 1/9
6. хlgх+2= 1000
Логарифмируя обе части уравнения (x > 0), получим:
(lgx+2)•lgx=lg1000
Lg2x+ 2lgx- 3=0
lgx=y
у2+ 2у- 3=0
y=- 3, у=1.
lgx=- 3, x=10-3=0,001;
lgx=1, x=10
Выполнив проверку, убедимся, что оба найденных значения переменной являются корнями данного уравнения.
Ответ: 0,001; 10.
7.Log16x+log4x+ log2x=7
(1/4)log2x+ (1/2)log2x+ log2x=7
(7/4)log2x=7
Log2x=4
x=16.
Ответ: 16.
8.Найти корни уравнения
Log3x=4-x
Так как функция у= log3х возрастающая, а функция у =4-х убывающая на
(0; + ∞), то заданное уравнение на этом интервале имеет один корень.
Ответ: 3
Домашнее задание:
1)Учебник «Алгебра и начала математического анализа 10-11 классы» Ш.А.Алимов п.19 стр.105-109
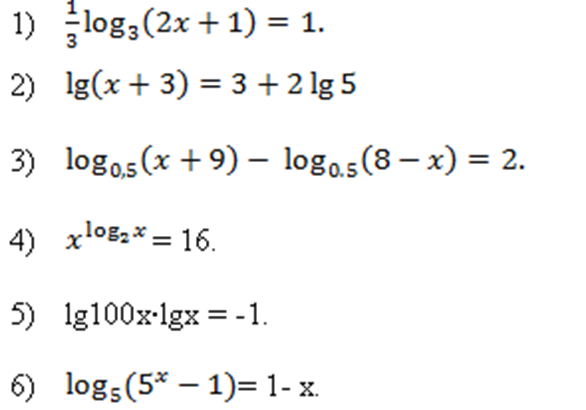
Критерии оценивания:
1.Оценка «отлично» - выставляется обучающемуся, если правильно решены все задания, выполнены в полной мере, изложены логично.
1. Оценка «хорошо» - выставляется обучающемуся, если допущены незначительные погрешности в задании.
2. Оценка «удовлетворительно» - выставляется обучающемуся, если ответ на вопрос нелогичный, не полный.
3. Оценка «неудовлетворительно» - выставляется обучающемуся, если задания не решены.
ВНИМАНИЕ!!!
Уважаемые студенты, практическое задание необходимо выполнить в рабочей тетради (сфотографировать) или в формате Документа Word. Отправлять для проверки в личные сообщения на страницу ВКонтакте: https://vk.com/kolomiyetssg?z=photo95751036_324720501%2Falbum95751036_0%2Frev
Преподаватель: Коломиец Светлана Григорьевна