Внутренняя энергия тела (термодинамической системы) может изменяться при совершении работы и в процессе теплопередачи. Закон сохранения и превращения энергии, распространенный на тепловые явления называется первым законом термодинамики (первым началом термодинамики) и записывается в виде
. (10.1)
Здесь Q — количество теплоты, сообщенное системе. Q считается положительным, если система в процессе теплопередачи получает энергию, и отрицательным, если отдает энергию.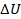 
— изменение внутренней энергии системы, A — работа, совершаемая системой над окружающими телами. В зависимости от характера процесса Q, 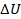и A могут быть любого знака и даже нулевыми.
Можно показать, что для любого идеального газа (одноатомного, двухатомного, многоатомного) изменение внутренней энергии 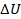в любом процессе можно находить по формуле
. (10.2)
Здесь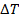 
— изменение температуры в этом процессе, 
— число молей газа, 
— молярная теплоемкость газа при постоянном объеме. Молярная теплоемкость при постоянном объеме у всех одноатомных идеальных газов одна и та же: 
Молярные теплоемкости при постоянном объеме у всех двухатомных идеальных газов равны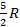 
, а у трехатомных и многоатомных (атомы у которых расположены не на одной прямой) — 3R: Удельные же теплоемкости у всех одноатомных идеальных газов различные и зависят от молярной массы. Аналогично для двухатомных и многоатомных газов.
Пример 10.1. Одноатомный идеальный газ в количестве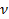 
= 2моль перевели из состояния 1 с температурой T 1 = 300 K в состояния 2 с температурой T 2 = 400 K в процессе с зависимостью давления от объема, изображенной на рис. 7.2. Найти изменение внутренней энергии газа.
|
|
Решение. 
.
Пример 10.2. При расширении двух молей одноатомного идеального газав цилиндре под поршнем от газа отвели 200 Дж теплоты и газ совершил работу 250 Дж. Найти изменение температуры газа.
Решение. У насQ= -200Дж,A= 250Дж,= 2моль, = 
.По первому закону термодинамики .
Отсюда 
Температура понизилась на 18 К.
Пример 10.3. Два моля одноатомного идеального газа переводят изобарически из состояния 1 с температурой T 1 = 300 K в состояние 2 с температурой T 2 = 340 K. Затем газ изохорически переводят в состояние 3 с температурой T 3 = 310 K. Какое количество теплоты получил газ в процессе 1–2–3?
Решение. Для наглядности процесс в виде зависимости давления от объема V изображен на рис. 10.1. У нас = 2 моль. Обозначим в состояниях 1 и 2 через V 1 и V 2 объемы, а через P 1 общее давление. По первому закону термодинамики для процесса 1–2–3
.
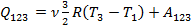Работа газа в процессе 1–2–3
A 123 = A 12 + A 23 = A 12 + 0 = A 12 = P 1 (V 2 -V 1):
Запишем уравнение состояния газа для точек 1 и 2:
P 1 V 1 = 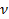RT 1, P 1 V 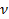2 = RT 2.
Из последних двух уравнений P 1 (V 2 -V 1) = 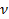R(T 2 -T 1). Тогда
,
.
Подстановка числовых значений дает 
.
Рис. 10.1.
Пример 10.4. Азот в количестве 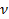= 3моль нагревают при постоянномдавлении от температуры T = 300 K. Какое количество теплоты сообщили газу, если его объем увеличился в 3 раза? Азот считать идеальным газом с молярной теплоемкостью при постоянном объеме 
.
Решение. ПустьP— давление,V— начальный объем,T 2 — конечнаятемпература. По первому закону термодинамики
,
где 
Запишем уравнение состояния газа для начального и конечного состояний:
|
|
, 
.
Отсюда 
, T 2 = 3T.
Тогда 
.