Понятие Комплесного числа.
В школьном курсе математики понятие числа постепенно расширяется. Сначала речь идет только о натуральных числах, затем последовательно появляются целые, рациональные и, наконец, действительные числа. В этой лекции понятие числа будет еще раз расширено: будут введены так называемые комплексные числа, включающие в себя действительные числа как весьма частный случай. В лекции рассматриваются операции над комплексными числами в алгебраической и тригонометрической форме. Более глубокое изучение комплексных чисел выходит за рамки нашего курса. Одной из причин расширения понятия числа является потребность в решении уравнений. В множестве натуральных чисел N неразрешимо даже такое простейшее уравнение, как x + 1 = 0, в множестве целых чисел Z — уравнение 2x = 1, в множестве рациональных чисел Q — уравнение x 2 = 2. В множестве действительных чисел R все эти уравнения имеют решение, но остается неразрешимым такое простое уравнение, как, например, x 2 + 1 = 0. Как мы увидим в этой лекции, в множестве комплексных чисел C это уравнение разрешимо. Более того, как мы узнаем в следующей лекции, в множестве C разрешимо любое алгебраическое уравнение с одним неизвестным.
Комплексное число имеет вид a + bi; здесь a и b – действительные числа, а i – число нового рода, называемое мнимой единицей.
Действительное число a назовем абсциссой комплексного числа a + bi; действительное число b – ординатой комплексного числа a + bi. Основное свойство числа i состоит в том, что произведение i*i равно –1, т.е.
i2= -1. (1)
Действительное число а записывается также в виде a + 0i (или a – 0i).
Геометрическое изображение комплексных чисел
 Выбираем на плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях (рис. 1). Комплексное число a + bi изображаем точкой М, у которой абсцисса х равна абсциссе а комплексного, а ордината у равна ординате b комплексного числа.
Выбираем на плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях (рис. 1). Комплексное число a + bi изображаем точкой М, у которой абсцисса х равна абсциссе а комплексного, а ордината у равна ординате b комплексного числа.
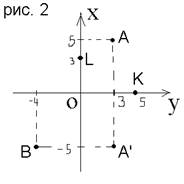
Примеры. На рис. 2 точка А с абсциссой х=3 и ординатой у=5 изображает комплексное число 3 + 5i. Точка В (-4,-5) изображает комплексное число –4 - 5i.
Действительные числа (в комплексной форме они имеют вид a + 0i) изображают точками оси OХ, а чисто мнимые – точками оси OУ.
Примеры. Точка К на рис. 2 изображает действительное число 5, точка L – чисто мнимое число 3i. Начало координат изображает число 0.
Сопряжённые комплексные числа изображаются парой точек, симметричных относительно оси абсцисс; так, точки А и А’ на рис. 2 изображают сопряжённые числа 3 +5i и 3 -5i.
Комплексные можно изображать также отрезками, начинающимися в точке О и оканчивающимися в соответствующей точке числовой плоскости. Так, комплексное число a + bi можно изобразить не только точкой M (рис. 1), но также вектором ОM.
Действия с комплексными числами
Сложение комплексных чисел
Определение Суммой двух комплексных чисел 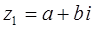 и
и 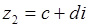 называется комплексное число
называется комплексное число 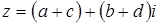 .
.
Числа 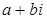 и
и 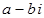 называются сопряженными. Их сумма равна действительному числу 2 а,
называются сопряженными. Их сумма равна действительному числу 2 а, 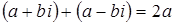 .
.
Числа 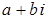 и
и 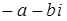 называются противоположными. Их сумма равна нулю.
называются противоположными. Их сумма равна нулю.
Комплексные числа равны, если равны их действительные части и коэффициенты мнимых частей: 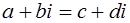 , если
, если 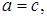
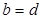 .
.
Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т. е. 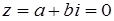 , если
, если 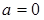 ,
, 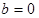 . Действительные числа являются частным случаем комплексных чисел. Если
. Действительные числа являются частным случаем комплексных чисел. Если 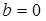 , то
, то 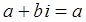 – действительное число.
– действительное число.
Если 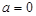 ,
, 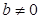 , то
, то 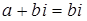 – чисто мнимое число. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
– чисто мнимое число. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
Вычитание комплексных чисел определяется как действие, обратное сложению: разностью двух комплексных чисел 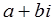 и
и 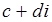 называется комплексное число
называется комплексное число 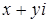 , которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел, получим два уравнения, из которых найдем, что
, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел, получим два уравнения, из которых найдем, что 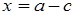 ,
, 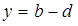 .
.
Значит, 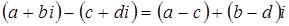
Пример 1. (-3 + 5i) + (4 – 8i) = 1 - 3i
Пример 2. (2 + 0i) + (7 + 0i) = 9 + 0i. Так как запись 2 + 0i означает то же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой (2 + 7=9).
Пример 3. (0 + 2i) + (0 + 5i) = 0 + 7i, т. е. 2i + 5i = 7i
Пример 4. (-2 + 3i) + (- 2 – 3i) = - 4
В примере 4 сумма двух комплексных чисел равна действительному числу. Два комплексных числа a+bi и a-bi называются сопряженными. Сумма сопряженных комплексных чисел равна действительному числу.
Вычитание комплексных чисел.
Определение. Разностью комплексных чисел a + bi (уменьшаемое) и c + di (вычитаемое) называется комплексное число (a – c) + (b – d)i.
Пример 1. (-5 + 2i) – (3 – 5i) = -8 + 7i
Пример 2. (3 + 2i) – (-3 + 2i) = 6 + 0i = 6
Умножение комплексных чисел.
Определение. Произведение комплексных чисел 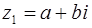 и
и 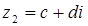 называется комплексное число
называется комплексное число
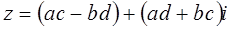 ,
,
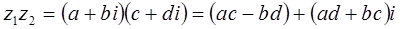 .
.
Легко проверить, что умножение комплексных чисел можно выполнять как умножение многочленов с заменой i 2 на –1. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному положительному числу: 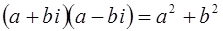 .
.
Замечание. На практике нет нужды пользоваться формулой произведения. Можно перемножить данные числа, как двучлены, а затем положить, что i2 = -1.
Пример 1. (1 – 2i)(3 + 2i) = 3 – 6i + 2i – 4i 2 = 3 – 6i + 2i + 4 = 7 – 4i.
Пример 2. (a + bi)(a – bi) = a2 + b 2
Деление комплексных чисел.
Деление комплексных чисел, кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем:
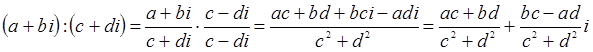
Степень числа i является периодической функцией показателя с периодом 4.
Действительно, 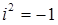 ,
, 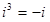 ,
, 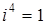 ,
, 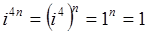 ,
, 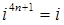 ,
, 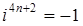 ,
, 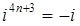 .
.
Можно использовать следующие соотношения, связывающие сопряженные комплексные числа: 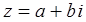 ,
, 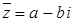 ,
, 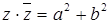 ,
, 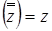 .
. 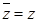
Пример 1. Найти частное (7 – 4i):(3 + 2i).
Записав дробь (7 – 4i)/(3 + 2i), расширяем её на число 3 – 2i, сопряженное с 3 + 2i. Получим:
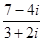 =
= 
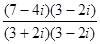 =
= 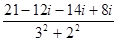 =
= 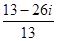 =1-2i
=1-2i