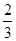Часть 1. Построение сечения многогранника. Площадь сечения (периметр).

Задачи для зачета по геометрии.

1. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD с ос­но­ва­ни­ем ABCD про­ве­де­но се­че­ние через се­ре­ди­ны ребер АВ и ВС и вер­ши­ну S. Най­ди­те пло­щадь этого се­че­ния, если все ребра пи­ра­ми­ды равны 8.

Ответ:

2. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD с ос­но­ва­ни­ем ABCD про­ве­де­но се­че­ние через се­ре­ди­ны рёбер AB и BC и вер­ши­ну S. Най­ди­те пло­щадь этого се­че­ния, если бо­ко­вое ребро пи­ра­ми­ды равно 5, а сто­ро­на ос­но­ва­ния равна 4. Ответ: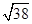

3. В тре­уголь­ной пи­ра­ми­де MABC, в ос­но­ва­ни­и ко­то­рой лежит пра­виль­ный тре­уголь­ник ABC, ребро MB пер­пен­ди­ку­ляр­но плос­ко­сти ос­но­ва­ния, сто­ро­ны ос­но­ва­ния равны 6, а ребро MA равно 11. На ребре AC на­хо­дит­ся точка D, на ребре AB точка E, а на ребре AM — точка F. Из­вест­но, что AD = 4 и BE = 2, F — се­ре­ди­на AM. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки E, D и F. Ответ: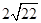

4. В тре­уголь­ной пи­ра­ми­де MABC ос­но­ва­ни­ем яв­ля­ет­ся пра­виль­ный тре­уголь­ник ABC, ребро MB пер­пен­ди­ку­ляр­но плос­ко­сти ос­но­ва­ния, сто­ро­ны ос­но­ва­ния равны 3, а ребро MA = 6. На ребре AC на­хо­дит­ся точка D, на ребре AB точка E, а на ребре AM — точка L. Из­вест­но, что AD = AL = 2, и BE = 1. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки E, D и L. Ответ:

5. В пра­виль­ной тре­уголь­ной пи­ра­ми­де MABC с ос­но­ва­ни­ем ABC сто­ро­ны ос­но­ва­ния равны 6, а бо­ко­вые рёбра 8. На ребре AC на­хо­дит­ся точка D, на ребре AB на­хо­дит­ся точка E, а на ребре AM — точка L. Из­вест­но, что СD = BE = LM = 2. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки E, D и L.

Ответ: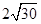

6. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC бо­ко­вое ребро SA = 5, а сто­ро­на ос­но­ва­ния AB = 4. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через ребро AB пер­пен­ди­ку­ляр­но ребру SC.

Ответ:

7. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де MABCD с вер­ши­ной M сто­ро­ны ос­но­ва­ния равны 3, а бо­ко­вые рёбра равны 8. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точку B и се­ре­ди­ну ребра MD па­рал­лель­но пря­мой AC. Ответ: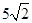

8. В пра­виль­ной тре­уголь­ной приз­ме ABCA ₁ B ₁ C ₁ сто­ро­ны ос­но­ва­ния равны 6, бо­ко­вые рёбра равны 4. Изоб­ра­зи­те се­че­ние, про­хо­дя­щее через вер­ши­ны A, B и се­ре­ди­ну ребра A ₁ C ₁. Най­ди­те его пло­щадь.

Ответ:

9. Точка E — се­ре­ди­на ребра BB ₁ куба ABCDA ₁ B ₁ C ₁ D ₁. Най­ди­те пло­щадь се­че­ния куба плос­ко­стью D ₁ AE, если ребра куба равны 4. Ответ: 18

10. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA ₁ B ₁ C ₁ D ₁, из­вест­ны рёбра: AB = 3, AD = 2, AA ₁ = 5. Точка O при­над­ле­жит ребру BB ₁ и делит его в от­но­ше­нии 2: 3, счи­тая от вер­ши­ны B. Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки A, O и C ₁. Ответ:

11. В пра­виль­ной тре­уголь­ной пи­ра­ми­де MABC с вер­ши­ной M вы­со­та равна 6, а бо­ко­вые рёбра равны 9. Най­ди­те пло­щадь се­че­ния этой пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через се­ре­ди­ны сто­рон AC и BC па­рал­лель­но пря­мой MC. Ответ: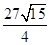

12. В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де PABCD, все ребра ко­то­рой равны 4, точка K ― се­ре­ди­на бо­ко­во­го ребра AP.

а) По­строй­те се­че­ние пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точку K и па­рал­лель­ной пря­мым PB и BC.

б) Най­ди­те пло­щадь се­че­ния. Ответ: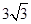

13. В ос­но­ва­нии пра­виль­ной тре­уголь­ной приз­мы ABCA ₁ B ₁ C ₁лежит тре­уголь­ник со сто­ро­ной 8. Вы­со­та приз­мы равна 3. Точка N — се­ре­ди­на ребра A ₁ C ₁.

а) По­строй­те се­че­ние приз­мы плос­ко­стью BAN. б) Най­ди­те пло­щадь этого се­че­ния. Ответ: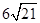

14. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD с ос­но­ва­ни­ем ABCD про­ве­де­но се­че­ние через се­ре­ди­ны рёбер AB и BC и вер­ши­ну S. Най­ди­те пло­щадь этого се­че­ния, если бо­ко­вое ребро пи­ра­ми­ды равно 5, а сто­ро­на ос­но­ва­ния равна 4. Ответ: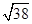

15. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де MABCD с вер­ши­ной M сто­ро­ны ос­но­ва­ния равны 1, а бо­ко­вые рёбра равны 2. Точка N при­над­ле­жит ребру MC, причём MN: NC = 2:1. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки B и N па­рал­лель­но пря­мой AC. Ответ: