Часть 2. Расстояние от точки до плоскости, от точки до прямой.

1. Дан куб ABCDA ₁ B ₁ C ₁ D ₁. Длина ребра куба равна 1. Найдите расстояние от середины отрезка BC ₁ до плоскости AB ₁ D ₁. Ответ:

2. Дана правильная четырехугольная пирамида SABCD. Боковое ребро , сторона основания равна 2. Найдите расстояние от точки B до плоскости ADM, где M — середина ребра SC. Ответ: 1

3. Дана правильная четырехугольная пирамида SABCD. Боковое ребро , сторона основания равна 2. Найдите расстояние от точки S до плоскости ADM, где M — середина ребра SC. Ответ: 1

4. В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 5, а сторона основания равна 6. Найдите расстояние от вершины A до плоскости SBC.

Ответ:

5. Основанием прямого параллелепипеда ABCDA ₁ B ₁ C ₁ D ₁ является ромб ABCD, сторона которого равна 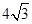, а угол ВАD равен 60°. Найдите расстояние от точки А до прямой C ₁ D ₁, если известно, что боковое ребро данного параллелепипеда равно 8. Ответ: 10

6. В правильной шестиугольной призме ABCDEFA ₁ B ₁ C ₁ D ₁ E ₁ F ₁ все рёбра равны 1. Найдите расстояние от точки B до плоскости DEA ₁. Ответ: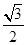

7. В правильной четырехугольной призме ABCDA ₁ B ₁ C ₁ D ₁ высота равна 1, а сторона основания равна . Точка M — середина ребра AA ₁. Найдите расстояние от точки M до плоскости DA ₁ C ₁.

Ответ: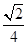

8. Ребро SA пирамиды SABC перпендикулярно плоскость основания ABC. Найдите расстояние от вершины A до плоскости, проходящей через середины рёбер AB, AC и SA, если .

Ответ: 1

Часть 3. Угол между скрещивающимися прямыми, угол между прямой и плоскостью.

1. Точка E — се­ре­ди­на ребра CC ₁ куба ABCDA ₁ B ₁ C ₁ D ₁. Най­ди­те угол между пря­мы­ми BE и B ₁ D.

Ответ:

2. На ребре CC ₁ куба ABCDA ₁ B ₁ C ₁ D ₁ от­ме­че­на точка E так, что CE: EC ₁ = 1: 2. Най­ди­те угол между пря­мы­ми BE и AC ₁. Ответ:

3. В пра­виль­ном тет­ра­эд­ре ABCD най­ди­те угол между вы­со­той тет­ра­эд­ра DH и ме­ди­а­ной BM бо­ко­вой грани BCD. Ответ:

4. Бо­ко­вое ребро пра­виль­ной тре­уголь­ной пи­ра­ми­ды SABC равно 6, а ко­си­нус угла ASB при вер­ши­не бо­ко­вой грани равен 1/9. Точка M — се­ре­ди­на ребра SC. Най­ди­те ко­си­нус угла между пря­мы­ми BM и SA.

Ответ:

5. Сто­ро­на пра­виль­ной тре­уголь­ной приз­мы ABCA ₁ B ₁ C ₁ равна 8. Вы­со­та этой приз­мы равна 6. Найти угол между пря­мы­ми CA ₁ и AB ₁. Ответ:

6. Длина ребра пра­виль­но­го тет­ра­эд­ра ABCD равна 1. Най­ди­те угол между пря­мы­ми DM и CL, где M — се­ре­ди­на ребра BC, L — се­ре­ди­на ребра AB.

Ответ:

7. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA ₁ B ₁ C ₁ D ₁ най­ди­те угол между плос­ко­стью A ₁ BC и пря­мой BC ₁, если AA ₁ = 8, AB = 6, BC = 15. Ответ:

8. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA ₁ B ₁ C ₁ D ₁, у ко­то­ро­го AA ₁ = 4, A ₁ D ₁ = 6, C ₁ D ₁ = 6, най­ди­те тан­генс угла между плос­ко­стью ADD ₁ и пря­мой EF, про­хо­дя­щей через се­ре­ди­ны ребер AB и B ₁ C ₁.

Ответ:

9. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с ос­но­ва­ни­ем ABC из­вест­ны рёбра: AB =21 , SC = 29. Най­ди­те угол, об­ра­зо­ван­ный плос­ко­стью ос­но­ва­ния и пря­мой, про­хо­дя­щей через се­ре­ди­ны рёбер AS и BC.

Ответ:

10. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA ₁ B ₁ C ₁ D ₁ най­ди­те угол между плос­ко­стью AA ₁ C и пря­мой A ₁ B, если AA ₁ = 3, AB = 4, BC = 4. Ответ:

11. Ос­но­ва­ни­ем пря­мой приз­мы ABCA ₁ B ₁ C ₁ яв­ля­ет­ся рав­но­бед­рен­ный тре­уголь­ник ABC, AB = AC = 5, BC = 8. Вы­со­та приз­мы равна 3. Най­ди­те угол между пря­мой A ₁ B и плос­ко­стью BCC ₁. Ответ: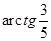

12. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA ₁ B ₁ C ₁ D ₁ из­вест­ны AB = 2, AD = AA ₁ = 1. Най­ди­те угол между пря­мой AB ₁ и плос­ко­стью ABC ₁. Ответ: