Мономолекулярная (МММ) и бимолекулярная (БММ) модели используются для расчета кислородного режима водоёмов, а также для определения динамики изменения количества растворенной в воде органики (для чего используется критерий БПК).
Задача сводится к изучению кислородного баланса на основе рассматриваемых процессов: потребление кислорода на окисление органического вещества и реаэрация через поверхность раздела вода-воздух.
Процесс описывается системой уравнений Фелпса-Стритера. Система имеет ограниченный диапазон применимости: при больших дефицитах кислорода в условиях анаэробного режима кривая кислородного прогиба, построенная по уравнениям Фелпса-Стритера даёт количественно неправдоподобную картину – отрицательное значение величины концентрации кислорода в воде, чего, естественно, быть не может. Отсюда следует, что при такой концентрации БПК применять моно молекулярную модель нельзя. В этом случае можно использовать бимолекулярную или тримолекулярную модель.
Мономолекулярная модель записывается в виде:
,
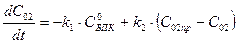где С1 – концентрация органических загрязнений по БПК, мг/л;
С2 – концентрация растворённого в воде кислорода, мг/л;
С2ПР. – предельное содержание растворённого в воде кислорода при данной температуре, мг/л;
k1 – коэффициент биохимического окисления (минерализации), 1/сут;
k2 – коэффициент реаэрации (обогащением кислородом), 1/сут;
t – время, сут.
Бимолекулярная модель записывается в виде:
,
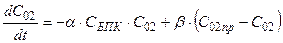где a - коэффициент биохимического окисления для бимолекулярной модели;
- коэффициент реаэрации по бимолекулярной модели.
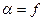(T, 0C, характеристики веществ, концентрации кислорода), 
.
Алгоритм решения задачи
|
|
1) Проверка применимости МММ при начальных значениях БПК.
2) Если МММ применима, то:
а) решение задачи при начальных значениях БПК;
б) определение концентрации кислорода и БПК на расстоянии L при заданной v.
3) Если МММ не применима, то:
а) решение МММ при измененных концентрациях БПК;
б) проверка применимости МММ при измененных значениях БПК.
4) МММ применима, тогда:
а) решение МММ при измененных концентрациях БПК;
б) решение МММ и БММ при измененных концентрациях БПК. Определение коэффициента ά;
в) решение БММ при найденном коэффициенте ά и исходных концентрациях БПК;
г) определение концентраций кислорода и БПК на расстоянии L при заданной v.
I этап
При начальной концентрации БПК решаем мономолекулярную модель.
По результатам решения строим график (рис 1).
Рис.1 График зависимости величины кислорода и БПК от времени, построенный по результатам расчетов с использованием мономолекулярной модели (МММ) при Со2нач=7мг/л и СБПКнач=40 мг\л.
Решение может быть верным, т.к. область значения кислорода не уходит в отрицательную область. Таким образом, при данных значениях кислорода и БПК мономолекулярная модель применима, но возможно использование и бимолекулярной модели.
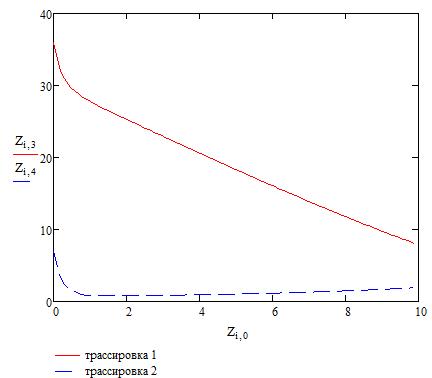
Рис.2 График зависимости величины кислорода и БПК от времени, построенный по результатам расчетов с использованием бимолекулярной модели (БММ) при Со2нач=11мг/л и СБПКнач=36 мг\л.
Будем подбирать значения начальных концентраций так, чтобы выполнялись нормативы в заданном контрольном створе. А без подбора концентраций БПК и кислорода имеем следующий результат:
|
|
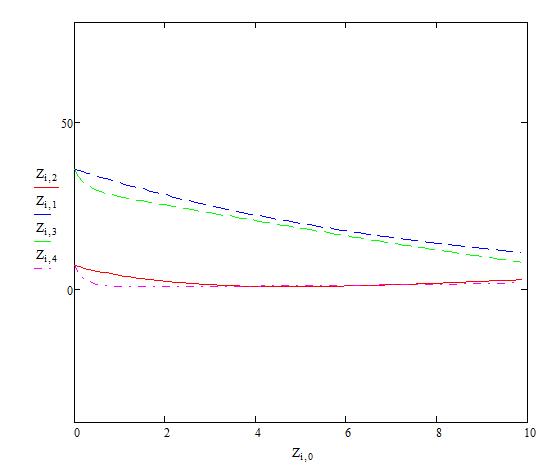
Рис.3 Графики зависимостей концентраций БПК и кислорода от времени, построенные по результатам расчетов с использованием МММ и БММ при заданных начальных условиях (для КС=2 ПДК не выполнено)
II этап
Так как нам дано расстояние до контрольного створа и скорость течения воды, то мы можем рассчитать время изменения параметров (2 суток) и сравнить их с предельно допустимыми (ПДКО2=6 мг/л; ПДКБПК=3 мг/л). Изменяем начальное значение концентрации БПК до 3 мг/л, а кислорода до 6 мг/л. Имеем:
Рис.4 Графики зависимостей концентраций БПК и кислорода от времени, построенные по результатам расчетов с использованием МММ и БММ при измененных начальных условиях (для Кс=2 ПДК выполнено)
Данное решение верно, т.к. значения кислорода не уходят в отрицательную область. Видим, что решения по МММ и БММ практически совпадают, значит в данной задаче применимы обе модели. Причем к1= α.