Имеются следующие выборочные данные по предприятиям одной из отраслей промышленности региона в отчетном году (выборка 20 % - ная, механическая), млн. руб.:
| № предприятия | Выпуск продукции | Среднегодовая стоимость основных производственных фондов | № предприятия | Выпуск продукции | Среднегодовая стоимость основных производственных фондов |
| 36.45 | 34.714 | 36.936 | 34.845 | ||
| 23.4 | 24.375 | 53.392 | 46.428 | ||
| 46.540 | 41.554 | 41.0 | 38.318 | ||
| 59.752 | 50.212 | 55.680 | 47.590 | ||
| 41.415 | 38.347 | 18.2 | 19.362 | ||
| 26.86 | 27.408 | 31.8 | 31.176 | ||
| 79.2 | 60.923 | 39.204 | 36.985 | ||
| 54.720 | 47.172 | 57.128 | 48.414 | ||
| 40.424 | 37.957 | 28.44 | 28.727 | ||
| 30.21 | 30.21 | 43.344 | 39.404 | ||
| 42.418 | 38.562 | 70.720 | 55.25 | ||
| 64.575 | 52.5 | 41.832 | 38.378 | ||
| 51.612 | 45.674 | 69.345 | 55.476 | ||
| 35.42 | 34.388 | 35.903 | 34.522 | ||
| 14.4 | 16.0 | 50.220 | 44.839 |
Задание 1
1. Постройте статистический ряд распределения организаций по признаку – эффективность использования основных производственных фондов – фондоотдача (для её нахождения необходимо разделить выпуск продукции на среднегодовую стоимость основных производственных фондов), образовав 5 групп с равными интервалами.
1.1. Находим эффективность использования основных производственных фондов – фондоотдачу:
| № пред- приятия | Выпуск продук- ции | Среднегодовая стоимость основных производствен-ных фондов | Эффективность использования основных производственных фондов - фондоотдача | № пред- приятия | Выпуск продук- ции | Среднегодовая стоимость основных производствен-ных фондов | Эффективность использования основных производственных фондов - фондоотдача |
| 36.45 | 34.714 | 1.05 | 36.936 | 34.845 | 1.06 | ||
| 23.4 | 24.375 | 0.96 | 53.392 | 46.428 | 1.15 | ||
| 46.540 | 41.554 | 1.12 | 41.0 | 38.318 | 1.07 | ||
| 59.752 | 50.212 | 1.19 | 55.680 | 47.590 | 1.17 | ||
| 41.415 | 38.347 | 1.08 | 18.2 | 19.362 | 0.94 | ||
| 26.86 | 27.408 | 0.98 | 31.8 | 31.176 | 1.02 | ||
| 79.2 | 60.923 | 1.3 | 39.204 | 36.985 | 1.06 | ||
| 54.720 | 47.172 | 1.16 | 57.128 | 48.414 | 1.18 | ||
| 40.424 | 37.957 | 1.06 | 28.44 | 28.727 | 0.99 | ||
| 30.21 | 30.21 | 43.344 | 39.404 | 1.1 | |||
| 42.418 | 38.562 | 1.1 | 70.720 | 55.25 | 1.28 | ||
| 64.575 | 52.5 | 1.23 | 41.832 | 38.378 | 1.09 | ||
| 51.612 | 45.674 | 1.13 | 69.345 | 55.476 | 1.25 | ||
| 35.42 | 34.388 | 1.03 | 35.903 | 34.522 | 1.04 | ||
| 14.4 | 16.0 | 0.9 | 50.220 | 44.839 | 1.12 |
1.2. Ранжируем ряд распределения предприятий по возрастанию (по признаку - эффективность использования основных производственных фондов):
| № предприятия | Эффективность использования основных производственных фондов - фондоотдача | Ранг | № предприятия | Эффективность использования основных производственных фондов - фондоотдача | Ранг |
| 1.05 | 1.06 | ||||
| 0.96 | 1.15 | ||||
| 1.12 | 1.07 | ||||
| 1.19 | 1.17 | ||||
| 1.08 | 0.94 | ||||
| 0.98 | 1.02 | ||||
| 1.3 | 1.06 | ||||
| 1.16 | 1.18 | ||||
| 1.06 | 0.99 | ||||
| 1.1 | |||||
| 1.1 | 1.28 | ||||
| 1.23 | 1.09 | ||||
| 1.13 | 1.25 | ||||
| 1.03 | 1.04 | ||||
| 0.9 | 1.12 |
1.3. Определяем размах вариации по формуле: R=Xmax-Xmin, где Xmax – максимальное значение признака (эффективность использования основных производственных фондов – фондоотдача) в ранжированном ряду, а Xmin – минимальное значение признака в ранжированном ряду, то есть:
R=1.3-0.9=0.4 млн. руб.
Далее находим число групп в группировке по формуле Стерджесса:
n=1+3.322lnN, где N – это число единиц совокупности (в нашем случае N=30):
n=1+3.322ln30=1+3.322*1.477=5 групп
Затем определяем величину интервала: i=R/n:
i=0.4/5=0.08 млн. руб.
Определим интервалы и число групп в них:
| 0.9 – 0.98 | |
| 0.98 – 1.06 | |
| 1.06 – 1.14 | |
| 1.14 – 1.22 | |
| 1.22 – и более |
1.4. Построим интервальный ряд распределения предприятий по эффективности использования основных производственных фондов (таблица 1).
Таблица 1. Группировка предприятий по эффективности использования основных производственных фондов.
| Группы предприятий по эффективности использования основных производственных фондов, млн. руб. | Число предприятий в группе |
| 0.9 – 0.98 | |
| 0.98 – 1.06 | |
| 1.06 – 1.14 | |
| 1.14 – 1.22 | |
| 1.22 – и более |
Интервальный ряд распределения показал, что наибольшее количество предприятий имеют эффективность использования основных производственных фондов от 1.06 до 1.14 млн. руб.
2. Постройте графики полученного ряда распределения. Графически определите значения моды и медианы. По данным таблицы 1 строим гистограмму распределения предприятий по эффективности использования основных производственных фондов (рис.1).
Рис. 1. Гистограмма распределения предприятий по эффективности использования основных производственных фондов.
Далее, соединяя середины верхних оснований столбцов, получаем полигон распределения.
Теперь графически необходимо определить значения моды и медианы. Мода – это наиболее часто встречающаяся варианта совокупности. На графике она будет выглядеть так (рис.2.):
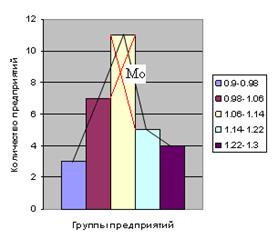
Рис. 2. Мода
Медиана – это варианта, делящая ряд пополам. Для её графического изображения построим кумуляту и рассчитаем кумулятивно – накопленные частоты в таблице. (таблица 2)
Таблица 2. Кумулятивно - накопленные частоты использования основных производственных фондов.
| Группы предприятий по эффективности использования основных производственных фондов, млн. руб. | Число предприятий в группе | Кумулятивно – накопленные частоты |
| 0.9 – 0.98 | ||
| 0.98 – 1.06 | ||
| 1.06 – 1.14 | ||
| 1.14 – 1.22 | ||
| 1.22 – и более |
Рис.3. Кумулятор распределения предприятий по эффективности использования основных производственных фондов
Модальным будет являться третий интервал, так как его кумулятивная частота равна 21 (3+7+11), что превышает половину суммы всех частот (30/2=15). (Рис. 3.)
Вывод: медиана = 1.07 млн. руб. показывает, что половина предприятий имеет эффективность использования основных производственных фондов < 1.07 млн. руб., а вторая >1.07 млн. руб. Мода показывает, что наибольшее часто встречаются в совокупности предприятия с эффективностью использования основных производственных фондов 1.09-1.14 млн. руб.
3. Рассчитайте характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.
По данным интервального ряда составим расчетную таблицу 3.
Таблица 3. Расчётная таблица
| Группы предприятий по эффективности использования основных производственных фондов, млн. руб. | Число предприятий в группе | Середина интервала Xi | 
| 
|
| 0.9 – 0.98 | 0.94 | 0.0256 | 0.0768 | |
| 0.98 – 1.06 | 1.02 | 0.0064 | 0.0448 | |
| 1.06 – 1.14 | 1.1 | |||
| 1.14 – 1.22 | 1.18 | 0.0256 | 0.032 | |
| 1.22 – и более | 1.26 | 0.0064 | 0.1024 |
3. 1. Находим середины интервалов Xi:
1) (0.9+0.98)/2=0.94; 2) (1.06+1.14)/2=1.1; 4) (1.14+1.22)/2=1.18; 5)
(1.22+1.3)/2=1.26
3. 2. Так как у нас имеются сгруппированные данные, представленные в виде интервального ряда распределения, то для нахождения средней арифметической и среднего квадратического отклонения будем использовать формулы для взвешенной средней:
где ∑fi – это общая численность единиц совокупности; ∑Xi * fi – это сумма произведений величины признаков на их частоты.
Следовательно,
Xар. взв. =(0.94*3+1.02*7+1.1*11+1.18*5+1.26*4)/30=1.1млн. руб.
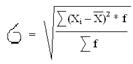
Для вычисления среднего квадратического отклонения необходимо вычислить некоторые составляющие формулы: (Xi – X)2 и (Xi – X)2 * f. (таблица 3).
1) (0.94-1.1)2 = 0.0256; 2) (1.02-1.1)2 = 0.0064; 3) (1.1-1.1)2 = 0; 4) (1.18-1.1)2 = 0.0064; 5) (1.16-1.1)2 = 0.0256.
1) 0.0256*3 = 0.0768; 2) 0.0064*7 = 0.0448; 3) 0*11 = 0;4) 0.0064*5 = 0.032; 5) 0.0256*4 = 0.1024.
Подставляем найденные значения в исходную формулу среднего квадратического отклонения, получаем:
млн. руб.
Теперь найдём коэффициент вариации:
Вывод: среднее значение эффективности использования основных производственных фондов предприятий в интервальном ряду по выборочной совокупности составляет 1.1 млн. руб. Значение эффективности использования основных производственных фондов отклоняется в среднем от этой средней величины на 
0.094 млн. руб. Таким образом, среднее значение эффективности использования основных производственных фондов является типичным для данной совокупности предприятий, а сама совокупность – однородной по данному показателю, так как V < 33%. 
4. Вычислите среднюю арифметическую по исходным данным, сравните её с аналогичным показателем, рассчитанным в пункте 3 для интервального ряда распределения. Объясните причину их расхождения.
где n – это число единиц совокупности, ∑X – сумма значений вариант.
Значение данной величины < значения средней арифметической взвешенной. Такие результаты в расчётах возможны в случае, если в интервальном ряду при расчёте средней взвешенной значение середины интервала Xi не совпадает с равномерным распределением этого интервального признака внутри группы, поэтому возникает расхождение.
Задание 2
По исходным данным:
1. Установите наличие и характер связи между признаками – выпуск продукции и эффективность использования основных производственных фондов, образовав пять групп с равными интервалами по обоим признакам, методами:
а) аналитической группировки,
б) корреляционной таблицы.
а) а.1. Построим аналитическую группировку по признаку - эффективность использования основных производственных фондов, (таблица 4)
Таблица 4. Аналитическая группировка по признаку - эффективность использования основных производственных фондов.
| Группы предприятий по эффективности использования основных производственных фондов, млн. руб. | Число предприятий в группе | Эффективность использования основных производственных фондов, млн. руб. | Выпуск продукции, млн. руб. | |||
| всего | в среднем в группе | всего | в среднем в группе | |||
| 0.9 - 0.98 | 2.8 | 2.8/3=0.933 | 56/3=18.667 | |||
| 0.98 - 1.06 | 7.11 | 7.11/7=1.016 | 225.083 | 225.083/7=32.155 | ||
| 1.06 - 1.14 | 11.99 | 11.99/11=1.09 | 474.945 | 474.945/11=43.177 | ||
| 1.14 - 1.22 | 5.85 | 5.85/5=1.17 | 280.672 | 280.672/5=56.134 | ||
| 1.22 - 1.3 | 5.06 | 5.06/4=1.265 | 283.84 | 283.84/4=70.96 | ||
| Итого: | 32.81 | 5.474 | 1320.54 | 221.093 |
а.2. Построим аналитическую группировку по признаку - выпуск продукции, (таблица 5):
1. ранжируем ряд распределения предприятий по признаку – выпуск продукции по возрастанию.
| № предприятия | Выпуск продукции | Ранг | № предприятия | Выпуск продукции | Ранг |
| 36.45 | 36.936 | ||||
| 23.4 | 53.392 | ||||
| 46.540 | 41.0 | ||||
| 59.752 | 55.680 | ||||
| 41.415 | 18.2 | ||||
| 26.86 | 31.8 | ||||
| 79.2 | 39.204 | ||||
| 54.720 | 57.128 | ||||
| 40.424 | 28.44 | ||||
| 30.21 | 43.344 | ||||
| 42.418 | 70.720 | ||||
| 64.575 | 41.832 | ||||
| 51.612 | 69.345 | ||||
| 35.42 | 35.903 | ||||
| 14.4 | 50.220 |
2. Находим R=Xmax-Xmin =79.2-14.4=64.8 млн. руб.; n=1+3.322lnN= 1+3.322ln30=1+3.322*1.477=5 групп; i=R/n=64.8/5=12.96 млн. руб.
Определим интервалы и число групп в них:
| 14.4 – 27.36 | |
| 27.36 – 40.32 | |
| 40.32 – 53.28 | |
| 53.28 – 66.24 | |
| 66.24 – и более |
Таблица 5. Аналитическая группировка по признаку - выпуск продукции.
| Группы предприятий по выпуску продукции, млн. руб. | Число предприятий в группе | Выпуск продукции, млн. руб. | Эффективность использования основных производственных фондов, млн. руб. | ||
| всего | в среднем в группе | всего | в среднем в группе | ||
| 14.4 - 27.36 | 82.86 | 82.86/4=20.715 | 3.78 | 3.78/4=0.945 | |
| 27.36 - 40.32 | 274.363 | 274.363/8=34.295 | 8.25 | 8.25/8=1.031 | |
| 40.32 - 53.28 | 398.805 | 398.805/9=44.312 | 9.87 | 9.87/9=1.097 | |
| 53.28 - 66.24 | 345.247 | 345.247/6=57.541 | 7.08 | 7.08/6=1.18 | |
| 66.24 - и более | 219.265 | 219.265/3=73.088 | 3.83 | 3.83/3=1.277 | |
| Итого: | 1320.54 | 229.951 | 32.81 | 5.53 |
В аналитической группировке с ростом эффективности использования основных производственных фондов наблюдается увеличение выпуска продукции, то есть между двумя признаками существует прямая связь. И, наоборот, с ростом выпуска продукции увеличивается эффективность использования основных производственных фондов.
б) У нас имеются следующие данные:
R=Xmax-Xmin=1.3-0.9=0.4 млн. руб.; i=R/n=0.4/5=0.08 млн. руб.;
n=1+3.322lnN=1+3.322ln30=1+3.322*1.477=5 групп
R=Xmax-Xmin =79.2-14.4=64.8 млн. руб.; n=1+3.322lnN=1+3.322ln30=1+3.322*1.477=5 групп; i=R/n=64.8/5=12.96млн. руб.
По ним строим корреляционную таблицу: (таблица 6)
| 0.9 – 0.98 | |
| 0.98 – 1.06 | |
| 1.06 – 1.14 | |
| 1.14 – 1.22 | |
| 1.22 – и более | |
| 14.4 – 27.36 | |
| 27.36 – 40.32 | |
| 40.32 – 53.28 | |
| 53.28 – 66.24 | |
| 66.24 – и более |
Таблица 6. Корреляционная таблица.
| Группы предприятий по выпуску продукции, млн. руб. | Группы предприятий по эффективности использования основных производственных фондов, млн. руб. | |||||
| 0.9 - 0.98 | 0.98 - 1.06 | 1.06 - 1.14 | 1.14 - 1.22 | 1.22 - и более | Итого: | |
| 14.4 - 27.36 | 1,15,20(3) | 6(1) | ||||
| 27.36 - 40.32 | 10,14,21,24,29(5) | 22(1) | ||||
| 40.32 - 53.28 | 1(1) | 3,5,9,11,13,16,18,25,27,30(10) | ||||
| 53.28 - 66.24 | 4,8,19,23(4) | 12(1) | ||||
| 66.24 - и более | 17(1) | 7,26,28(3) | ||||
| Итого: |
Вывод: корреляционная таблица показывает наличие тесной взаимосвязи между признаками – выпуск продукции и эффективность использования основных производственных фондов, так как из таблицы видно, что концентрация предприятий наблюдается ближе к середине, все они располагаются достаточно близко друг к другу.
Задание 3
По результатам выполнения задания 1 с вероятностью 0.683 определите:
1. Ошибку выборки среднего уровня фондоотдачи и границы, в которых он будет находиться в генеральной совокупности.
2. Ошибку выборки доли организаций с уровнем фондоотдачи 1.14 млн. руб. и более и границы, в которых будет находиться генеральная доля.
1. Из расчётов задания 1 видно, что средняя эффективность использования основных производственных фондов составляет 1.1 млн. руб. Определим среднюю 
и предельную ошибки выборки 
. По расчетным данным дисперсия признака составляла 
2 =0.0942=0.0088 млн. руб. Отсюда:
, так как по условию выборка 20% - ная. N=n/0.2=150.
Теперь будем искать предельную ошибку выборки, млн. руб.:
= 
t *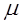 
, так как вероятность = 0.683, то t = 1. 
= 1*0.0153 = 0.0153. 
Теперь найдем границы, в которых будет находиться средний уровень фондоотдачи: Xар. взв. – 
X Xар. взв. + ; 1.0847 X 1.1153.
Вывод: с вероятностью 68.3% можно утверждать, что ошибка выборки среднего уровня фондоотдачи будет находиться в пределах от 1.0847 млн. руб. до 1.1153 млн. руб.
2. Определим долю предприятий с уровнем фондоотдачи 1.14 млн. руб. и более: 
= m/n=9/30=0.3, где m – количество предприятий, имеющих уровень фондоотдачи 1.14 млн. руб. и более.
Предельная ошибка для доли равна:
,
2w= 
(1- 
)=0.3*(1-0.3)=0.21
Теперь найдем границы, в которых будет находиться генеральная доля:
- 
w 
+ 
w, 0.2252 
0.3748.
Вывод: с вероятностью 68.3% можно утверждать, что средний уровень фондоотдачи 1.14 млн. руб. и более будет находиться в границах от 0.2252 млн. руб. до 0.3748 млн. руб.
Задание 4
Имеются следующие данные о наличии и движении основных производственных фондов организаций за год, млн. руб.:
Полная первоначальная стоимость на начало года 50.2
В течение года:
- введено новых…………………………………………………………..7.8
- выбыло по себестоимости за вычетом износа……………………….0.45
- полная стоимость выбывших фондов…………………………………4.8
Износ основных фондов на начало года, %..............................................20
Годовая норма амортизации, %...............................................................10
По приведенным данным:
1. Постройте баланс основных производственных фондов по полной стоимости; по данным этого баланса рассчитайте показатели движения основных фондов.
2. Постройте баланс основных фондов по остаточной стоимости; по данным этого баланса рассчитайте коэффициенты состояния основных производственных фондов на начало и конец года.
Сделайте выводы. 1. Построим баланс основных производственных фондов по полной стоимости, млн. руб. (таблица 7):
Таблица 7. Баланс основных фондов по полной стоимости.
| Наличие основных фондов на начало года | Поступило в отчетном году | Выбыло в отчетном году | Наличие основных фондов на конец года | ||
| всего | в том числе новых основных фондов | всего | с том числе ликвидировано | ||
| 50.2 | 7.8 | 7.8 | 4.8 | - | 50.2+7.8-4.8=53.2 |
Рассчитаем показатели, характеризующие движение основных фондов:
коэффициент обновления: Кобновления= 
= 
*100%=14.66%;
коэффициент выбытия: Квыбытия= 
= 
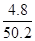*100%=9.56%.
2. Рассчитаем остаточную стоимость основных фондов на начало года:
Используя полученные данные, построим баланс основных фондов по остаточной стоимости, млн. руб. (таблица 8):
Таблица 8. Баланс основных фондов по остаточной стоимости.
| Наличие основных фондов на начало года | Поступило в отчетном году | Выбыло в отчетном году | Амортизация за год | Наличие основных фондов на конец года | ||
| всего | в том числе новых основных фондов | всего | с том числе ликвидировано | |||
| 40.16 | 7.8 | 7.8 | 0.45 | - | 50.2*0.1=5.02 | 40.16+7.8-0.45-5.02=42.49 |
Используя данные баланса, рассчитаем коэффициенты состояния основных производственных фондов на начало и конец года:
на начало года: Кизноса=20%(по условию). Следовательно, Кгодн на эту дату равен 80%(100%-20%); на конец года:
Кизноса= 
*100%=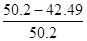 
*100%=15.36%;
Кгодности= 
*100%= 
*100%=84.64%, (или 100%-15.36%).
Вывод: при сравнении коэффициентов, характеризующих состояние основных фондов, следует обратить внимание на то, что износ основных фондов уменьшился (15.36%-20%=-4.64%). Это произошло вследствие ввода значительного объёма новых основных фондов.