Исходные данные для построения изоквант
| К | Q 01 = 400 | Q 01 = 445 | Q 01 = 490 | Q 01 = 535 |
| L1(K) = 301,0247 L1(K) = 272,4893 L1(K) = 252,2380 L1(K) = 236,8093 | L2(K) = 345,1145 L2(K) = 312,3997 L2(K) = 289,1825 L2(K) = 271,4937 | L3(K) = 390,4826 L3(K) = 353,4667 L3(K) = 327,1974 L3(K) = 307,1838 | L4(K) = 437,0424 L4(K) = 395,6129 L4(K) = 366,2116 L4(K) = 343,8113 |
По данным табл. 3.1 строим изокванты производственной функции. Видно, что переменная L оказывает на функцию значительно большее влияние, чем К.
3). Построение касательных к изоквантам в точках производства, отвечающих заданной величине вложенного капитала К 0 = 400.
Вначале рассчитаем координаты точек изоквант, отвечающих заданной величине вложенного капитала К 0 = 400. Из рисунка следует, что величине вложенного капитала К 0 = 400 отвечает одна изокванта: Q 02 = 445. В табл. 3.1 находим соответствующее ему значение затраченного труда L: L 02 = 312. Получаем координаты точек изоквант (К 0, L 0):
· изокванты Q 02 = 445 — (400; 312);
Уравнение касательной к изокванте 1,00 K 0,27 L 0,78 = Q 0 в точке (К 0, L 0) записывается так:
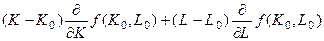= 0.
Находим частные производные:
= 
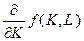=0,27x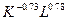 
;
= 
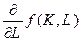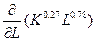=0,78x 
.
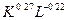В табл. 3.2 представлены результаты расчета параметров касательных для изокванты.
Таблица 3.2
Исходные данные для построения касательных
| Параметры касательных | |||||
| Изокванты | K 0 | L 0 |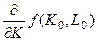 
| 
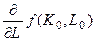
| Угловой коэффициент |
| Q 02 = 445 | 0,3 | 1,1112 | -3,704 |
Получаем следующее уравнение касательной:
· к изокванте Q 02 = 445: 0,3 (К - 400) + 1,1112 (L - 312) = 0;
Эти касательные представляют собой прямые, проходящие через точки с координатами (К 0, L 0) с отрицательным наклоном к оси L, равным отношению 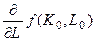/ 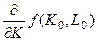с отрицательным знаком (последняя колонка табл. 3.2).
4). Интерпретация математических понятий по пп. 2—3.
Изокванты Q 01 = 400, Q 02 = 445, Q 03 = 490 и Q 04 = 535 представляют собой линии уровня функции Q двух переменных К и L: Q = f (К, L). Поскольку производственная функция Q = 1,00 K 0,27 L 0,78 возрастает с ростом обеих переменных, большим значениям Q отвечают изокванты, которые дальше отстоят от начала координат. Изокванты не пересекаются, так как Q = 1,00 K 0,27 L 0,78 является монотонной и однозначной функцией.
|
|
Касательными к изоквантам являются прямые линии, имеющие только одну общую точку с изоквантами. Угловой коэффициент касательных равен первой производной переменной L по переменной К при условии Q = const. Знак углового коэффициента отрицательный, т.е. при условии Q = const увеличение одной переменной должно быть скомпенсировано уменьшением другой переменной. Абсолютная величина углового коэффициента значительно больше единицы, что отражает большее влияние на функцию переменной L по сравнению с переменной К.
5). Расчет выпуска продукции, а также предельных продуктов труда и капитала для производства с заданными показателями (К 0, L 0) = (400; 320).
Расчет выпуска продукции производим по производственной функции подстановкой значений переменных К 0, L 0:
Q 0 = 1´(K 0)0,27(L 0)0,78 = 1´4000,273200,78 = 453,4996;
Расчет предельного продукта труда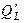 
и капитала 
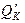производим по полученным ранее формулам:
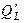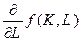= = 0,78´ 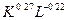; 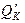= = 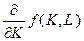0,27´ ,
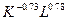однако в отличие от частных производных 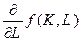и 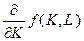, являющихся математическими понятиями и не имеющих размерности, предельные показател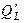и и 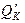имеют размерность единиц выпуска на единицу труда и капитала соответственно. Подставляя значения К 0 = 400 и L 0 = 320, получаем:
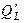(400; 320) = 0,78´ 
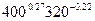= 1,1053 ед. продукции на ед. труда;
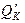(400; 320) =0,27´ 
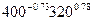= 0.306 ед. продукции на ед. капитала.
|
|
6). Расчет коэффициента заменяемости ресурсов для производства с заданными показателями (К 0, L 0) = (400; 320) производим по формуле R =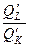 
:
R (400; 320) = 1,1053 / 0.306 = 3,6121 ед. капитала на ед. труда.
7). Расчет эластичности выпуска по труду и капиталу и производства в целом с заданными показателями (К 0, L 0) = (400; 320) производим по формулам:
EL =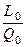 
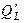(400; 320); EK =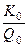 
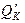(400; 320); E = EK + EL.
Подставляя значения К 0, L 0, 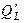, , 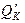получаем:
EL = 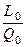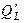(400; 320) = (320 /453,4996) ´ 1,1053 = 0,7799;
EK = 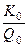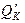(400; 320) = (400 /453,4996) ´ 0,306 = 0,2699;
E = EK + EL = 0,2699 + 0.7799 = 1,0498.
8). Интерпретация экономических понятий по пп. 5—7.
Предельные продукты труда и капитала в точке изокванты производственной функции Q 0 = 453,4996 единиц продукции соответственно равны 1,1053 ед. продукции на ед. труда и 0,306 ед. продукции на ед. капитала. Это интерпретируется так: производство продукции Q 0, характеризующееся величинами капитала К 0 = 400 ед. и труда L 0 = 320 ед., при увеличении труда L на одну ед. увеличивается на 1,1053 ед., а при увеличении капитала K на одну ед. увеличивается на 0,306 ед. Таким образом, увеличение труда является более эффективным.
Коэффициент заменяемости ресурсов в точке изокванты производственной функции Q 0 = 453,4996 единиц продукции составляет 3,6121 ед. капитала на ед. труда. Это означает, что для того, чтобы выпуск продукции не изменился, надо при уменьшении на единицу вложенного труда увеличить вложение капитала на 3,6121 единиц.
Эластичность выпуска по труду и капиталу производства с заданными показателями труда К 0 = 400 ед. и капитала L 0 = 320 ед. составляет 0,7799 и 0,2699 соответственно. Это означает, что при относительном увеличении (уменьшении) труда и капитала на 1% рост (снижение) выпуска продукции составит 0,7799% и 0,2699% соответственно.
|
|
Эластичность производства в целом составляет 1,0498. Это означает, что при одновременном относительном увеличении (уменьшении) труда и капитала на 1% рост (снижение) выпуска продукции составит 1,0498%. Производство в целом можно оценить как эффективное, поскольку при увеличении масштаба производства в k раз (увеличении капитала и труда в k раз) выпуск продукции увеличится в в 1,0498 k раз.