При расчете симметрично нагруженных мачт, работающих на центральное сжатие, определяется поперечное сечение мачты и производится проверка ее на устойчивость. Эта часть расчетов для трубчатой мачты выполняется в следующем порядке:
1. Определяют требуемую площадь поперечного сечения мачты:
F тр = S м / (φo m · R),
где S м – суммарное сжимающее усилие в мачте; φo – коэффициент продольного изгиба; m – коэффициент условий работы (для монтажных мачт принимается равным 0,9); R – расчетное сопротивление.
2. Находят расчетную длину мачты:
Н м= μ ·Н,
где μ – коэффициент приведения расчетной длины (см. прил. 8). Для монтажной мачты μ = 1.
3. Подбирают сечение стальной трубы (см. прил. 7) при условии F т 
F тр и определяют радиус инерции r т.
4. Вычисляют гибкость мачты:
λ= Н м/ r т,
причем должно выполнятся условие λ ≤ [λ], где [λ] – предельная гибкость (см. прил. 9). Для трубчатой мачты [λ]=180.
5. По прил. 10 определяют коэффициент продольного изгиба φ, соответствующий расчетной гибкости λ.
6. Полученное сечение трубы для мачты проверяют на устойчивость:
S м / (F т · φ) 
mR.
При соблюдении данного неравенства прочность и устойчивость мачты будут обеспечены при условии, что расчетная гибкость λ меньше предельной [λ]. В противном случае необходимо подобрать другое сечение стальной трубы, обеспечивающее соблюдение этих условий.
Пример 8. Рассчитать сечение вертикальной трубчатой мачты для подъема мостового крана массой G o = 24т, если высота мачты Н= 10м, действующее на мачту суммарное сжимающее усилие S м = 440 кН.
Решение:
1. Определяем требуемую площадь поперечного сечения мачты (задавшись предварительно φo = 0,4):
|
|
F тр= S м / (0,1 φo · m · R)=440/(0,1·0,4·0,9·210)=58 см2.
2. Расчетную длину мачты находим по формуле
Н μ= μ· Н =1·10=10 м.
3. По прил. 7 подбираем трубу диаметром 219х10мм с площадью сечения F тр = 65, 6 см2 и радиусом инерции r т = 7,4 см.
4. Гибкость мачты рассчитываем по формуле
λ = Н м / r т = 1000 / 7,4=135,1; 
=180; λ ≤ [λ].
5. По прил. 10 определяем коэффициент продольного изгиба:
φo=0,380.
6. Полученное сечение мачты проверяем на устойчивость:
S м / (F т· φo) mR,
S м / (F т· φo)=440 / (65,6·0,38)=17,65 кН/см2 = 176,5 МПа,
mR =0,9·210=189 МПа.
Условие выполняется.
РАСЧЕТ ПОРТАЛОВ И ШЕВРОВ
Две мачты, соединенные вверху ригелем, к которому прикреплены грузовые полиспасты, называются порталом (рис. 17). Стойки портала (мачты) имеют, как правило, шарнирные опоры. Стойки и ригель могут быть как трубчатого, так и решетчатого сечения. Порталы устанавливаются в вертикальном или наклонном положении, фиксируются вантами регулируемой длины, которые крепятся к якорям. Порталы широко используются в монтажной практике, особенно при установке тяжеловесного оборудования, имеющего значительные поперечные размеры.
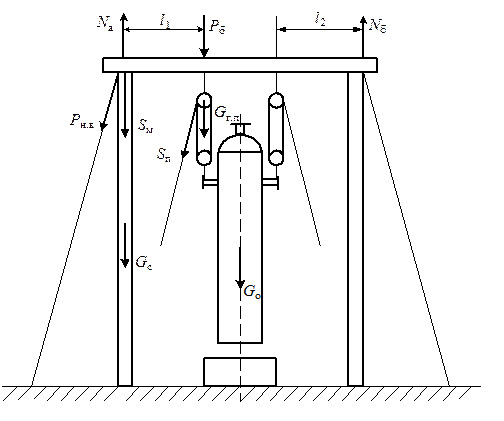
Рис. 17. Расчетная схема монтажного портала
Шевр представляет собой А-образную раму, состоящую из двух сборно-разборных трубчатых или решетчатых стоек, снабженных шарнирными опорами и соединенных вверху коротким ригелем (рис. 18). К ригелю крепятся два полиспаста, один – для подъема груза, другой – для опрокидывания шевра, если шевр используется как «падающий». Ригель шевра может крепиться к стойкам жестко или быть съемным.
|
|
Рис. 18. Расчетная схема монтажного шевра
Расчет портала сводится к следующему:
1. Определяют минимальную высоту портала Н аналогично монтажной мачте (см. п.10.1).
2. Подсчитывают усилие, действующее на каждый полиспаст:
P=G о / n,
где G о – масса поднимаемого оборудования; n – количество грузовых полиспастов.
3. Находят усилие, действующее на ригель в точке подвески полиспаста,
Р р = Р·К п ·К д +G г.п ·К п +S п,
где G г.п – масса грузового полиспаста; S п – усилие в сбегающей ветви полиспаста.
4. Определяют максимальный изгибающий момент в ригеле. Для данной схемы погружения изгибающий момент без учета собственной массы ригеля
М max =Р р· l 1.
5. Вычисляют требуемый момент сопротивления поперечного сечения ригеля:
W тр =М max/ (0,1 m·R),
где m – коэффициент условий работы (см. прил. 4), для порталов m = 0,9; R – расчетное сопротивление при изгибе (см. прил. 3).
6. При изготовлении ригеля из двутавра, швеллера или трубы подбирают соответствующее сечение (см.прил. 5–7), чтобы выполнялось условие Wх W тр. При необходимости рассчитывают максимальный прогиб ригеля и сравнивают его с допускаемым.
7. Находят опорные реакции N а и N б от действия ригеля на стойку портала. При симметричной схеме нагружения, без учета массы самого ригеля
N а = N б =Р р.
8. Определяют суммарное сжимающее усилие, действующее по оси каждой стойки портала:
S м = N а +G с· К п +Р н.в · sin α,
где G с – масса стойки портала; Р н.в – сжимающее усилие от нерабочих вант (определяют как для монтажных мачт).
9. Дальнейший расчет стойки портала ведут аналогично расчету трубчатых или решетчатых мачт (см. п. 10.3).
|
|
Расчет шевра, представленного на рис.18, проводят в такой последовательности:
1. Определяют минимальную высоту шевра Н аналогично монтажной мачте (см. п.10.1).
2. Подсчитывают усилие в грузовом полиспасте Р г.п Для вертикального шевра это усилие рассчитывают как при подъеме оборудования способом поворота вокруг шарнира (см. п. 13.2).
3. Определяют суммарное сжимающие усилие, действующее вдоль шевра:
S м =Р г.п· К п· К д·сos β +Р р.в· К п· К д·сos γ +G р.п· К п +G г.п· К п +G ш· К п +S г.п,
где Р р.в – усилие в задней рабочей ванте, рассчитывают так же, как для вертикальной мачты (см. п.10.3); G г.п и G р.п – массы грузового и рабочего полиспастов; G ш – масса шевра (определяется в начале ориентировочно);
S г.п – усилие в сбегающей ветви грузового полиспаста (определяют при расчете полиспаста по. п.7).
4. Находят сжимающее усилие в стойке шевра:
N c =S м / 2.
5. Рассчитывают сечение стоек и проверяют их устойчивость как для трубчатой или решетчатой мачты (см. п.10.3).
6. Находят суммарное усилие, действующее на ригель Р р. Если полиспасты закреплены посредине ригеля (l 1= l 2), то можно считать, что Р р= S м.
7. Определяют изгибающий момент в ригеле шевра, пренебрегая массой самого ригеля:
N а= N б =0,5 Р р, М max= Р р· l p / 4,
где l p – длина ригеля (l 1= l 2= 
).
8. Вычисляют требуемый момент сопротивления поперечного сечения ригеля (см3):
W тр =М max / (0,1· m · R),
где m – коэффициент условия работы (см. прил. 4), для шевра m =0,9; R – расчетное сопротивление при изгибе (см. прил. 3).
9. По прил. 5–7 подбирают требуемое сечение стандартного профиля (трубы, шевра или двутавра) так, чтобы выполнялось условие Wх W тр .