Тема 15. Основы механики разрушений
Широкое внедрение новых конструкторских решений, конструкционных материалов и технологий в начале 20 века привело к появлению абсолютно нового явления – катастрофическому разрушению конструкций (судов, самолетов, турбин и др.) при нагрузках, существенно меньших расчетных. Основная причина оказалась в том, что при действии на конструкцию переменных нагрузок, в ее элементах возникают усталостные трещины, которые интенсивно развивались, вплоть до нарушения целостности конструкции.
Механикой разрушения обычно называют науку, исследующую закономерности развития трещины, а также прочность элементов конструкций при наличии трещин. В механике разрушения термином «трещина» принято обозначать всякую несплошность в материале, возникающую вследствие образования свободных ненагруженных поверхностей, смыкающихся с бесконечно малым радиусом. Такое определение носит достаточно общий характер. Одно из его достоинств состоит в том, что под него подходят не только сами трещины как таковые, но и многие иные повреждения, например, механические повреждения с рваными краями, царапины и т.п. Это позволяет применять к ним тот же математический аппарат и критерии, что и в случае обычных усталостных трещин.
Первоначальное предположение о том, что причиной разрушения конструкций при наличии трещин служит изменение рабочей площади сечения за счет трещины, оказалось несправедливым. В частности, проводились испытания на растяжение пластины толщиной t и шириной b с центральной трещиной длины 2a (рис. 15.1а). Определим предельную нагрузку Рр, предполагая, что трещина не влияет на напряженно – деформированное состояние (НДС) пластины, а лишь уменьшает площадь  поперечного сечения:
поперечного сечения:
|
|
 (15.1)
(15.1)
Разделим левую и правую части уравнения (15.1) на начальную площадь поперечного сечения пластины tb:
 (15.2)
(15.2)
где  - разрушающее напряжение в пластине, определенное без учета изменения НДС, а лишь при уменьшении площади поперечного сечения. Если бы эффект наличия трещины сводился только к уменьшению площади поперечного сечения, то все экспериментальные точки должны были лежать в окрестности прямой 1 (рис. 15.1б, где
- разрушающее напряжение в пластине, определенное без учета изменения НДС, а лишь при уменьшении площади поперечного сечения. Если бы эффект наличия трещины сводился только к уменьшению площади поперечного сечения, то все экспериментальные точки должны были лежать в окрестности прямой 1 (рис. 15.1б, где 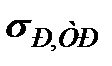 - разрушающие напряжения в пластине с учетом трещины). Однако испытания образцов из материалов Д16Т1 и В95Т1 показывают, что разрушение пластины с трещиной происходит при существенно меньших напряжениях (так, для сплава В95Т1 при длине трещины равной 0,5b разрушающие напряжения уменьшились почти в 2,5 раза, по сравнению с величиной, полученной за счет уменьшения площади поперечного сечения).
- разрушающие напряжения в пластине с учетом трещины). Однако испытания образцов из материалов Д16Т1 и В95Т1 показывают, что разрушение пластины с трещиной происходит при существенно меньших напряжениях (так, для сплава В95Т1 при длине трещины равной 0,5b разрушающие напряжения уменьшились почти в 2,5 раза, по сравнению с величиной, полученной за счет уменьшения площади поперечного сечения).
Так как до середины 60-х годов 20 века не были разработаны методы расчета на прочность при наличии трещины, то основные усилия были направлены на предотвращение их появления и замедлению развития.
Отметим наиболее интересные из этих решений:
- создание на пути развития трещин сжимающих усилий (насадка горячих колец на стволы орудий, намотка высокопрочной проволоки и др.);
- создание препятствий движению дислокаций внутри материала, путем легирования, создания мелкозернистых структур, применения наклепа;
- создание на пути трещин пластичных слоев. Например, русский кинжал был трехслойным – внутри прочный, но хрупкий материал, снаружи пластичный материал;
|
|
- засверливание трещин (подходит не для всех материалов), установка накладок и подкрепляющих элементов.
| b |
| 2a |
| σ |
| σ |
| σр,тр/σв |
| 0,8 |
| 0,6 |
| 0,4 |
| 0,2 |
| 2a/b |
| Д16Т1 |
| 0,2 |
| 0,4 |
| 0,6 |
| 0,8 |
| В95Т1 |
| а) |
| б) |
Рис. 15.1. Испытания пластины с трещиной
Проведенный анализ показывает, что для решения практических задач расчета конструкций при наличии трещин, а также прогнозирования их развития в процессе эксплуатации конструкции, необходимо было создать теоретические и экспериментальные основы данных расчетов. Первые шаги в решении поставленной задачи были сделаны в конце 19 – начале 20 века и связаны с исследованием явления концентрации напряжений. Так, в 1898 г. Г. Кирш решил задачу по определению НДС к растянутой пластине с центральным круговым отверстием. Оказалось, что напряжения на краю отверстия в три раза превысили значение напряжений вдали от отверстия. Увеличение напряжений в пластине с эллиптическим отверстием (Г.О. Колосов – 1909г., К. Инглис – 1913г.) было еще большим.
Используя данные результаты, в 1920г. А.А. Гриффитц разработал энергетический метод оценки прочности конструкции при наличии трещин. Суть метода заключается в том, что трещина будет расти и приведет к разрушению конструкции, если освобождаемая при росте трещины потенциальная энергия деформации будет больше, чем энергия, необходимая для образования новой свободной поверхности.
В 1957г. Дж.Р. Ирвингом был предложен силовой критерий разрушения и концепция квазихрупкого разрушения, позволившая перейти от идеального материала (теория Гриффитца) к реальным металлическим материалам и существенно упростить расчеты конструкций на прочность при наличии трещин.