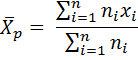Обработка результатов неравноточных измерений

Многократные измерения производятся в течение длительного времени. За это время могут измениться условия, появиться необходимость замены средства измерения или смена оператора. Это приводит к получению групп измерений с разными характеристиками погрешностей. Группы измерений, в которых измерение одной и той же величины производится разными методами и характеризуется разными погрешностями, называют неравноточными. Неравноточность объясняется различием неисключённых систематических погрешностей.

Если обработке подлежат ряды измерений, выполненные различными операторами или в разное время, то для оценки действительного значения измеряемой величины их необходимо проверить на равноточность. Для проверки равноточности двух рядов, состоящих из n₁ и n₂ измерений, вычисляют эмпирические дисперсии для каждого ряда:

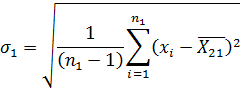
и

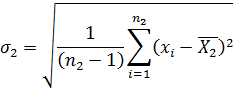
Затем находят дисперсионное отношение 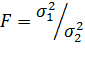при σ₁ ˃ σ₂. Измерения считаются равноточными при условии F ˃ F_q, где величины критерия F_q выбирается из таблиц в зависимости от уровня значимости q числа степеней свободы n₁ – 1 и n₂ – 1. Этот критерий называется критерием Фишера.

Для проверки равноточности результатов измерений применяют также критерий Романовского R. Для этого определяют отношение

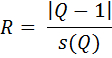
где

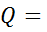
и

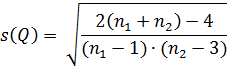
Результаты измерений считаются равноточными, если R < 3.

Обработка неравноточных измерений сводится к определению достоверного значения измеряемой величины и оценке воспроизводимости измерений.

Когда измерения одной и той же физической величины проводятся разными наблюдателями, на приборах разного класса и в течение нескольких дней, получаются несколько рядов измерений. В таких случаях при проверке равноточности нескольких рядов измерений должны учитываться т.н. “веса”, которые устанавливаются для каждой серии измерений

1. пропорционально вероятности,

2. либо числу измерений,

3. либо величине среднеквадратичного отклонения,

4. либо методом экспертных оценок.

Если ряды измерений (выборки) принадлежат одной генеральной совокупности, то границы доверительной вероятности устанавливают по распределению Стьюдента. Чем больше степень доверия к результатам, тем больше число, выражающее вес. Среднее взвешенное значение наиболее близкое к истинному равно:

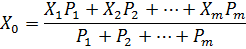
где X_i – средние значения для

отдельных групп наблюдений, а P_i – их ве са. Обычно веса соответствующих групп измерений считают обратно пропорциональными их средним квадратическим отклонениям: .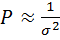

Тогда среднеквадратическая погрешность средневзвешенного значения будет равна:

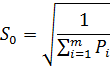
где P – вес каждого результата измерений, а m – число рядов измерений.

Общая формула обработки неравноточных измерений может быть выражена так

Пусть некоторая величина X была измерена многократно различными операторами и в разных условиях. В процессе измерений получены результаты x₁, x₁, … x_n со средними квадратичными отклонениями σ₁, σ₁, … σ_n

Наиболее вероятное значение 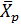может быть найдено по формуле:

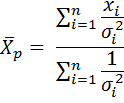
В эту формулу можно ввести веса экспериментальных точек. Вес:

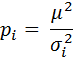
Где 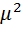коэффициент, выбранный таким образом, чтобы отношение 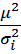было близким к единице.

Тогда формулу можно переписать так:

Среднее квадратичное отклонение результатов измерений вычисляется по формуле:

Для оценки среднего квадратичного отклонения средней взвешенной величины применяется формула:

Если σ_i не вычислялись, но известны средние значения измеряемой величины в каждой i – той серии (x_i) и количество наблюдений n_i то весовое среднее вычисляется по формуле: