Быстрое Преобразование Фурье с прореживанием по частоте
Цель работы.
Целью работы является ознакомление с алгоритмом Быстрого Преобразования Фурье (БПФ) с прореживанием по частоте.
Задания для выполнения лабораторной работы
Предварительная подготовка к выполнению лабораторной работы
2.1.1. Изучить описание к данной лабораторной работе и рекомендованную литературу.
2.1.2. Ознакомиться с основами Быстрого Преобразования Фурье с прореживанием по частоте.
2.1.3 Выполнить домашний расчёт, приведенный в данном описании лабораторной работы.
2.1.4 Подготовить письменный отчет принятой на кафедре формы. Отчет должен содержать:
- титульный лист принятой на кафедре формы;
- номера лабораторной работы, варианта работы и формулировку цели работы;
- исходные данные выполняемого варианта;
- домашний расчет;
- результат выполнения работы;
- краткие выводы по работе.
Выполнение исследований в лаборатории
Разделы выполнения лабораторной работы:
2.2.1. Создание проекта
2.2.2. Добавление источников VHDL
2.2.3. Моделирование проекта
Приложение
Быстрое преобразование Фурье
Для сокращения времени вычисления ДПФ используется «быстрый» алгоритм ДПФ – быстрое преобразование Фурье (fast Fourier transform - FFT) - БПФ.
Быстрое преобразование Фурье базируется на том, что при вычислениях, среди множителей (синусов и косинусов) есть много периодически повторяющихся значений (в силу периодичности функций). Алгоритм БПФ группирует слагаемые с одинаковыми множителями в пирамидальный алгоритм, значительно сокращая число умножений за счет исключения повторных вычислений. В результате быстродействие БПФ в зависимости от N может в сотни раз превосходить быстродействие стандартного алгоритма. При этом следует подчеркнуть, что алгоритм БПФ точнее стандартного, т.к. сокращая число операций, он приводит к уменьшению количества округлений, и как следствие, ошибки округления.
Основная идея, лежащая в основе этих алгоритмов, заключается в сведении вычисления исходного N –точечного ДПФ и вычислению нескольких N1 – точечных ДПФ, причем N1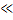 
N.
Пусть:
A = ac + ad + bc + bd – 4 умножения, 3 сложения;
A = a(c+d) + b(c+d) - 2 умножения, 3 сложения;
A = (a+d) (c+d) - 1 умножение, 2 сложения.
В приведенном примере мы сократили число операций путем «хитроумной» перестановки скобок в вычислениях
Наиболее распространенными являются алгоритмы с основанием 2, когда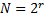 
кроме них используются алгоритмы с основанием 3,4,6 и др., будем рассматривать алгоритмы с основанием 2. Различают алгоритмы БПФ с прореживанием по времени и алгоритмы с прореживанием по частоте.
Алгоритмы, при реализации которых требуется перестановка отсчетов входной последовательности -- алгоритмы с прореживанием по времени.
Алгоритмы, при реализации которых требуется перестановка отсчетов выходной последовательности -- алгоритмы с прореживанием по частоте.
По эффективности алгоритмы равноценны, позволяют уменьшить число арифметических операций в 
раз по сравнению с прямым методом вычисления ДПФ.