Твердого тела
2. 1. Законы Ньютона
Динамика изучает механическое движение тел, учитывая их взаимодействие, которое является причиной изменения скорости движения тел, т. е. ускорения. Основу динамики составляют три закона Ньютона, сформулированные им в 1687 году. Законы Ньютона рассматривают как систему взаимосвязанных законов.
Первый закон. Существуют такие системы отсчета, в которых всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Утверждение, что существуют инерциальные системы отсчета, в которых ускорение материальной точки (тела) обусловлено только взаимодействием с другими телами, составляет содержание первого закона классической механики – закона инерции Галилея – Ньютона.
Существование инерциальных систем отсчета подтверждается опытом. Гелиоцентрическую систему отсчета принято считать инерциальной, потому любая система отсчета, которая движется равномерно и прямолинейно относительно этой системы, является также инерциальной. Системы отсчета, которые движутся с ускорением, называются неинерциальными. Уравнение движения в инерциальных системах отсчета имеет наиболее простой вид.
Второй закон Ньютона. Известно, что при одинаковых воздействиях тела приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его массы).
Масса тела – физическая величина, которая является мерой инертности и определяет инерционные и гравитационные свойства тел. В пределах классической механики масса:
Величина аддитивная, т. е. масса составного тела равна сумме масс его частей;
Величина постоянная.
Для описания взаимодействия тел вводят понятие силы. Сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.
Второй закон Ньютона отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Ускорение, приобретаемое телом, пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе тела
(2.1)
или
(2.2)
Так как масса тела в классической механике величина постоянная, ее можно внести под знак производной:
(2.3)
Векторная величина, равная произведению массы тела на его скорость, называется импульсом (количеством движения) этого тела
(2.4)
Тогда
(2.5)
Это выражение называется уравнением движения материальной точки и является более общей формулировкой второго закона Ньютона: скорость изменения импульса материальной точки (тела) равна действующей на нее силе.
Если на материальную точку (тело) действует несколько сил, то ее ускорение обусловлено результирующей силой, т. е.
(2.6)
Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: силы, с которыми тела действуют друг на друга, всегда равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей эти точки:
(2.7)
где 
– сила, действующая со стороны первого тела на второе;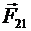 
– сила, действующая со стороны второго тела на первое.
Эти силы приложены к разным телам, всегда действуют парами и являются силами одной природы.
Работа. Мощность
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между телами в механике вводится понятие работы силы.
Если тело движется прямолинейно и на него действует постоянная сила 
, которая составляет угол a с вектором перемещения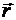 
(рис. 2.1), то работа этой силы равна:
(2.8)
или, учитывая, что в случае прямолинейного движения 
, имеем:
(2.9)
| 
|
| Рис. 2.1 | Рис. 2.2 |
В общем случае сила может изменяться как по модулю, так и по направлению (рис. 2.2). Рассматривая элементарное перемещение 
, в пределах которого силу 
можно считать постоянной, а движение точки – прямолинейным, элементарная работа 
определяется как скалярное произведение 
(2.10)
Интегрируя выражение (2.10), определим работу силы на участке траектории от точки 1 до точки 2:
(2.11)
Работа силы может быть как положительной, так и отрицательной в зависимости от угла a между векторами и (при 
работа силы положительна, при 
работа силы отрицательна, если 
, то работа силы равна нулю).
Геометрический смысл выражения (2.11) следует из графика на рис. 2.3. Элементарная работа на бесконечно малом участке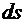 
равна площади заштрихованного прямоугольника.
| Работа на всем участке пути равна сумме элементарных работ  , т. е. определяется площадью фигуры 1–2–3–4. Для характеристики скорости, с которой соверша-
|
| Рис. 2.3 |
ется работа, вводят понятие мощности
(2.12)
Так как 
, то мощность равна скалярному произведению вектора силы на вектор скорости:
(2.13)
Механическая энергия
Физическая величина, характеризующая способность тела совершать работу, называется энергией.
Сила , действуя на покоящееся тело и вызывая его движение, совершает работу , которая идет на увеличение кинетической энергии тела 
,
(2.14)
Так как 
то
(2.15)
Учитывая, что скорость первая производная от перемещения по времени, получим
(2.16)
Из формул (2.14) и (2.16) видно, что
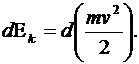(2.17)
Интегрируя это выражение, получаем:
(2.18)
При 
видим, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Тело обладает потенциальной энергией, находясь в потенциальном поле сил (например, упругих или гравитационных сил).
Потенциальное поле – это поле, в котором действуют консервативные силы.
Консервативные силы – силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положениями тела. Работа консервативных сил по замкнутой траектории равна нулю.
Если работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной (неконсервативной); ее примером является сила трения.
Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
(2.19)
Так как , то
(2.20)
Откуда
(2.21)
Конкретный вид функции потенциальной энергии зависит от характера силового поля. Например, потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна (рис. 2.4)
(2.22)
| Так как начало отсчета берется произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Найдем потенциальную энергию упруго деформированного тела (пружина). Сила уп- |
| Рис. 2.4 |
ругости пропорциональна деформации:
(2.23)
(2.24)
Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
В общем случае материальная точка (тело) может обладать одновременно и кинетической и потенциальной энергией.
Полная механическая энергия системы – энергия механического движения и взаимодействия равна сумме кинетической и потенциальной энергий
(2.25)
Так, например, тело массой m, находящееся на высоте h над поверхностью Земли и движущееся со скоростью v, обладает полной энергией
(2.26)
Законы сохранения
Законы сохранения относятся к числу фундаментальных законов физики. Эти законы универсальны, они действуют в микро- и макромире. Законы сохранения не зависят ни от траекторий частиц, ни от характера действующих сил и выполняются в изолированных системах. Их применение позволяет получить ряд весьма общих заключений о процессах, происходящих в системе, не решая уравнений движения.
Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной).
Закон сохранения энергии: полная механическая энергия системы тел, между которыми действуют только консервативные силы, остается постоянной
(2.27)
Потенциальная и кинетическая энергии могут превращаться друг в друга. Рассмотрим случай свободного падения тела с высоты h. До начала падения механическая энергия равна потенциальной энергии 
. В процессе падения тела увеличивается его кинетическая энергия (увеличивается скорость тела) и уменьшается потенциальная, т. е. происходит переход потенциальной энергии в кинетическую:
(2.28)
Полная энергия тела остается неизменной (сопротивлением воздуха пренебрегаем).
Если в системе кроме консервативных действуют также диссипативные силы (например, силы трения), то закон сохранения энергии будет иметь вид
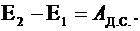(2.29)
где 
– работа диссипативных сил.
Наличие сил трения в замкнутой системе приводит к уменьшению ее полной механической энергии. Действие сил трения приводит к превращению механической энергии в другие виды энергии (например, внутреннюю энергию). В этом случае выполняется более общий закон сохранения энергии: в изолированной от любых внешних воздействий системе остается постоянной сумма всех видов энергии.
Закон сохранения импульса
Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой.
Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки действуют внешние тела, – внешними.
Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны m1, m2, … mn и 
, … 
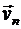. Пусть 
… 
– равнодействующие внутренних сил, действующие на каждое из тел, а … – равнодействующие внешних сил.
Запишем второй закон Ньютона для каждого из тел:
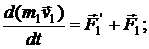
(2.30)
......
Складывая выражения (2.30), получим:
(2.31)
Согласно третьему закону Ньютона сумма внутренних сил равна нулю и выражение (2.31) примет вид:
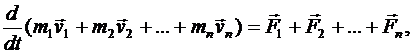(2.32)
или
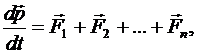(2.33)
где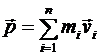 
– импульс системы.
В замкнутой системе (при отсутствии внешних сил)
т. е. 
(2.34)
Это выражение и является законом сохранения импульса: в замкнутых системах векторная сумма импульсов взаимодействующих тел остается постоянной.
Закон сохранения импульса выполняется и для незамкнутых систем, если геометрическая сумма всех внешних сил равна нулю.
Рассмотрим применение законов сохранения импульса и энергии при столкновении двух шаров. Силы взаимодействия между сталкивающимися телами столь велики, что внешними силами можно пренебречь и рассматривать систему тел в процессе соударения как замкнутую.
Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс.
Абсолютно упругим называется удар, при котором тела не деформируются. Для абсолютно упругого удара выполняются законы сохранения импульса и энергии
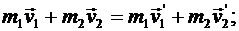(2.35)
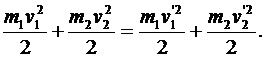(2.36)
Абсолютно неупругий удар – удар, в результате которого тела объединяются, двигаясь дальше как единое целое.
| 
|
| Рис. 2.5 | Рис. 2.6 |
Используя закон сохранения импульса, можно записать:
(2.37)
Вследствие деформации тела происходит «потеря» кинетической энергии, которая переходит в тепловую или другие формы энергии. Эту «потерю» энергии можно определить по разности кинетической энергии тел до и после удара:
(2.38)
Абсолютно неупругий удар – пример того, как происходит «потеря» механической энергии под действием диссипативных сил.