Определение современной стоимости денег включает:
· дисконтирование будущих потоков;
· определение наращенной суммы вложений;
· эрозия капитала.
Проценты и дисконтирование - основные приемы долгосрочного анализа. В основе их использования лежит понимание того, что с экономической точки зрения бессмысленно напрямую (без приведения к одному временному периоду) сопоставлять денежные суммы, получаемые в разное время. При этом не имеет значения, к какому моменту времени будут приводиться денежные суммы - настоящему или будущему. Однако, поскольку необходимость сопоставления денежных потоков возникает с целью принятия конкретного управленского решения, например об инвестировании денежных средств с целью получения дохода в будущем, денежные потоки, как правило, приводятся к моменту принятия решения (его принято называть момент времени 0).
Величина процентной ставки определяется балансом спроса и предложения, степенью риска и величиной инфляции. Кроме того, процентная ставка учитывает фактор времени, так как деньги, относящиеся к разным моментам времени, неравноценны. Согласно принципу неравноценности денег во времени, современные деньги ценнее будущих.
Будем использовать следующие обозначения:
t = 0 - момент предоставления денег в долг (настоящий момент времени);
T или n - срок долга;
Pt - сумма, предоставленная в долг в момент времени t;
P0 - сумма, предоставленная в долг в момент времени t = 0;
St - сумма погашаемого долга в момент t;
i - процентная ставка (наращения);
d - учетная ставка.
Предоставление денег в долг, как правило, связано с одной из двух операций - наращения или дисконтирования денежной суммы. Операция наращения применяется тогда, когда заданы сумма первоначального долга P0, процентная ставка и срок долга T. Требуется найти сумму погашаемого долга ST.
Определение. Процесс увеличения суммы долга в связи с присоединением к нему начисленных процентов называется наращением суммы первоначального долга.
Найденную наращением сумму погашаемого долга называют наращенной суммой долга.
Операция дисконтирования применяется тогда, когда задана сумма погашаемого долга ST, которую следует уплатить через время T, а также процентная ставка. Требуется найти сумму первоначального долга P0. В этом случае говорят, что сумма ST дисконтируется или учитывается.
Определение. Процесс уменьшения суммы погашаемого долга в связи с начислением и удержанием процентов называется дисконтированием или учетом погашаемого долга, а сами начисленные и удержанные проценты называются дисконтом.
Найденную дисконтированием сумму первоначального долга P0 называют современной или приведенной к моменту t = 0 величиной погашаемого долга ST. Таким образом, современная величина суммы ST, подлежащей выплате через время T, это сумма денег P0, которая, будучи вложенной в момент t = 0, через время T даст сумму ST.
Определение. Проценты, или процентные деньги, - это абсолютная величина дохода от предоставления денег в долг на время T.
Если доход определяется операцией наращения, то проценты вычисляют по формуле
I(T) = ST – P0. (3.1.)
Если доход определяется операцией дисконтирования, то проценты называют дисконтом и вычисляют по формуле
D(T) = ST – P0. (3.2)
В финансовой математике различают два вида ставок начисления процентов: процентная ставка и учетная ставка. Пусть t* - фиксированный отрезок времени (например: 1 месяц, 6 месяцев, 1 год), P0 - сумма, предоставленная в долг в момент t = 0 на время t*,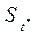 
- сумма погашаемого долга в момент t*.
Определение. Процентная ставка i за период t* - это отношение дохода за время t* к сумме вложенных средств:
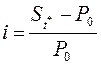(3.3)
Определение. Учетная ставка d за период t* - это отношение дохода за время t* к сумме погашаемого долга:
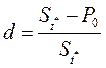(3.4)
Обе ставки выражаются в процентах или десятичных дробях.
Определение. Отрезок времени t*, к которому приурочена процентная ставка, называется периодом начисления процентов. В операции наращения период начисления процентов называют также периодом наращения. В операции дисконтирования период начисления процентов называют также периодом дисконтирования.
В зависимости от выбранного отрезка t* процентную ставку называют ежемесячной, полугодовой, годовой и т.д. При этом подразумевается однократное начисление процентов по этой ставке за период. Чаще всего применяется годовая процентная ставка.
Определение. Число 
называется числом периодов начисления процентов в сроке долга T.
Если срок долга измеряется в числе периодов начисления процентов n, то отрезок t*, т.е. один период начисления процентов, принимается за единицу измерения времени, а ставки i и d называют процентными ставками за единицу времени. При этом сумма погашаемого долга обозначается через Sn. В этих обозначениях
(3.5)
(3.6)
Формулы (3.5), (3.6) (как и (3.3), (3.4)) означают существование двух принципов расчета процентов. Рассмотрим инвестирование суммы P0 в момент t = 0 на один период. Как следует из (3.5), в момент t = 1, т.е. в конце периода, инвестору будет возвращена сумма S1 = P0 + i×P0. При этом сумма i×P0, выплачиваемая в момент t = 1, это проценты I(1) = S1 – P0 = i×P0 за время [0, 1] на заем величиной P0 в момент t = 0. Таким образом, проценты по ставке i начисляются на сумму первоначального долга P0 в момент t = 1.
Согласно (3.6), в обмен на возврат суммы S1 в момент t = 1 инвестор даст взаймы сумму P0 = S1 – d×S1. В этом случае проценты по ставке d начисляются в начальный момент времени t = 0 на сумму погашаемого долга S1. Сумма P0 может рассматриваться как заем суммы S1, возвращаемой через единицу времени, при котором проценты величиной d×S1 выплачиваются заранее, в момент t = 0, и составляют доход кредитора D(1) = S1 – P0 = d×S1 за время [0, 1].
Таким образом, проценты по ставке i начисляются в конце периода начисления процентов, а проценты по учетной ставке d - в начале периода начисления процентов.
Проценты различают по базе для их начисления.
Определение. Процентная ставка называется простой, если на каждом периоде база для начисления процентов является постоянной.
Определение. Процентная ставка называется сложной, если на каждом периоде базой для начисления процентов является сумма, полученная на предыдущем периоде наращения или дисконтирования.
4. Методы наращения по ставке i
Рассмотрим задачу. На банковский счет размещена сумма P0 под годовую ставку i без промежуточных выплат на счет или со счета. Какова будет сумма вклада через n лет?
1) Наращение по простой ставке i
Здесь t = 0 - момент размещения суммы P0 на банковский счет. Единица измерения времени - 1 год. Как следует из (3.5), проценты за первый год вклада равны I1 = i×P0. Согласно определению простой процентной ставки, проценты за каждый год вклада одинаковы и равны
I1 = I2 = … = In = i×P0. (4.1.)
Накопленные проценты за весь срок вклада n лет составят
I(n) = I1 + I2 + … + In = n×i×P0. (4.2)
Тогда наращенная сумма вклада через n лет станет равной
Sn = P0 + I(n).
Отсюда
S n = P0 (1 + i × n). (4.3)
Таким образом, если через n лет счет закрывается, то инвестору выплачивается сумма P0(1 + i×n). Этот платеж состоит из возврата исходного вложения P0 и процентов I(n) = n×i×P0. (4.3.) - формула наращенной суммы долга по простой процентной ставке i в течение n периодов. I1, I2,…, In – проценты за каждый период (единицу времени). В формуле (4.3) n необязательно целое. Нормальная коммерческая практика по отношению к дробным периодам года заключается в платеже процентов на пропорциональной основе. Это позволяет рассматривать выражения (4.2) и (4.3) как применимые ко всем неотрицательным значениям n. Формулой (4.3) обычно пользуются, если срок долга меньше года. Если i - годовая ставка, t - число дней в сроке долга, то 
, где K – число дней в году (временная база). Правила выбора временной базы и подсчета числа дней в сроке долга подробно рассмотрены в литературе.
Как следует из равенств (4.1.), особенностью простых процентов является то, что проценты, будучи зачисленными на счет, сами по себе не зарабатывают дальнейших процентов.
Пример 4.1. В конце третьего квартала сумма вклада стала равной 180 д.е. Найти величину годовой процентной ставки, по которой начислялись проценты в сумме 5 д.е. за каждый квартал.
Так как проценты начисляются в конце каждого квартала, то за единицу измерения времени можно принять 1 квартал. Тогда в конце каждого квартала проценты начисляются по квартальной процентной ставке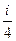 
, где i - годовая процентная ставка. Срок вклада n = 3 квартала (единицы времени). Наращенная сумма вклада Sn = 180 д.е. Проценты за каждый квартал (единицу времени) составляют I1 = I2 = I3 = 5 = I. Следовательно, для наращения вклада применяется простая процентная ставка. Проценты за весь срок вклада I(n) = n×I = 15 д.е. Так как Sn = P0 + I(n), то сумма первоначального вклада P0 = Sn – I(n) = 165 д.е. Поскольку 
, то годовая процентная ставка по вкладу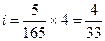 
.
Замечание. Пользуясь только условиями задачи, найти сумму вклада в конце второго квартала. Полученный ответ проверить по формуле (4.3).
2) Наращение по сложной ставке i
Будем считать, что в момент t = 0 сумма P0 размещена на банковский счет под сложную годовую процентную ставку. Согласно определению сложной процентной ставки, базой для начисления процентов на каждом периоде является сумма, полученная на предыдущем периоде наращения.
Следовательно, проценты за каждый год вклада составляют: I1 = i×P0, I2 = i×S1, …, In–1 = i×Sn–2, In = i×Sn–1, где S1, …, Sn–2, Sn–1 - суммы вклада в конце соответствующего периода наращения. Очевидно, что
S1 = P0 + I1,…, Sn–1 = Sn–2 + In–1, Sn = Sn–1 + In. (4.4)
Рассмотрим выражения для процентов:
I1 = i×P0,
I2 = i×S1 = i×(P0 + I1) = i×P0 + i×I1 = I1 + i×I1 = I1(1 + i),
………..
In = i×Sn–1 = i×(Sn–2 + In–1) = i×Sn–2 + i×In–1 = In–1 + i×In–1 = In–1(1 + i).
Таким образом,
I2 = I1(1 + i),
……….. (4.5)
In = In–1(1 + i).
Следовательно, I1, I2, …, In - члены геометрической прогрессии с первым членом I1 и знаменателем (1 + i). Проценты за весь срок вклада составляют I(n) = I1 + I2 + … + In. По формуле суммы n членов геометрической прогрессии находим
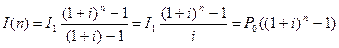. (4.6)
Наращенная сумма вклада через n лет станет равной Sn = P0 + I(n). Отсюда
(4.7)
Если инвестор закроет свой счет через n лет, он получит сумму P0(1 + i)n.
Этот платеж состоит из возврата исходного вклада P0 вместе с накопленными процентами (4.6). (4.7) - формула наращенной суммы долга при начислении сложных процентов по ставке i в течение n периодов. I1, I2,…, In - проценты за каждый период (единицу времени). Выражение (4.7) остается верным для всех неотрицательных значений n.
Как видим из (4.5), особенностью сложных процентов является то, что проценты сами зарабатывают проценты. Вследствие этого влияние сложных процентов на накопление на счете может быть очень значительным, особенно если длительность счета или процентная ставка велики.
Пример 4.2. Какова сумма первоначального вклада, размещенного под сложную процентную ставку, если проценты за первый и второй годы соответственно составили 20 и 21,6 д.е.?
Используем полученные соотношения для сложных процентов. Если единицей измерения времени является 1 год, то I1 = 20 д.е., I2 = 21,6 д.е., I2 = I1(1 + i), где i - годовая процентная ставка. Отсюда i = 0,08. Так как I1 = i×P0, то сумма первоначального вклада P0 = 250 д.е.
Замечание. Сделать проверку, вычислив I2 по определению. Найти I5, I7, S5, S7. Как они называются?
3) Наращение суммы вклада по номинальной ставке
Если сложные проценты начисляются не один, а m раз в году, то годовую процентную ставку называют номинальной и обозначают через i(m).
Общее определение номинальной процентной ставки будет рассмотрено позже. В случае начисления процентов m раз в году годовую номинальную процентную ставку можно определить следующим образом.
Определение. Годовая процентная ставка i(m) называется номинальной, если для начисления сложных процентов за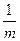 
часть года применяется ставка 
.
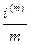Таким образом, если сложные проценты начисляются через равные промежутки времени m раз в году, то в конце каждого периода длиной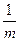 
проценты начисляются по ставке 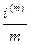. Если срок долга n лет, то m×n - число периодов применения ставки 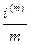в сроке долга. Из формулы (4.7) получаем
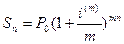,(4.8)
где m ≥ 1. Если m = 1, то i(1) = i, т.е. номинальная ставка совпадает с годовой ставкой сложных процентов, применяемой раз в году. (4.8) – формула наращенной суммы долга по номинальной ставке i(m) при начислении сложных процентов m раз в году в течение n лет.
4) Непрерывное начисление сложных процентов
Непрерывное начисление процентов - это начисление процентов за бесконечно малые отрезки времени, т.е. при 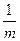→ 0 (или при m → ∞). При непрерывном начислении сложных процентов, когда m → ∞, годовую номинальную процентную ставку обозначают через δ и называют силой роста или интенсивностью процентов, а также непрерывной процентной ставкой. Таким образом, процентная ставка при непрерывном начислении процентов δ - это годовая номинальная процентная ставка при начислении процентов за бесконечно малые отрезки времени.
Перейдем к пределу при m → ∞ в выражении (4.8), учитывая, что при m → ∞ годовую номинальную процентную ставку обозначают через δ:
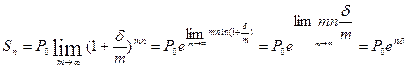
Таким образом,
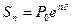(4.9)
(4.9) – формула наращенной суммы долга при постоянной интенсивности процентов в единицу времени δ в течение n периодов. Хотя это математическая идеализация реальности, процессы начисления процентов часто бывает удобно рассматривать как непрерывные.
Пример 1.3. Сравнить сроки удвоения суммы 1000 д.е. при начислении сложных процентов по годовой номинальной процентной ставке 0,1 а) по полугодиям; б) ежеквартально; в) непрерывно.
Согласно условию, P0=1000 д.е.,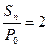 
, а) m=2, i(2)=0,1; б) m=4, i(4)=0,1; в) m→∞, δ=0,1. Из формул (4.8) и (4.9) получаем 
для случаев а), б) и в случае в)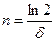 
.
Отсюда находим, что первоначальная сумма 1000 д.е. вырастет до 2000 д.е. за а) 7,103 года или 7 лет и 38 дней; б) 7,018 года или 7 лет и 6 дней; в) 6,931 года или 6 лет и 340 дней. Как видим, с увеличением частоты начисления процентов в году срок удвоения суммы уменьшается.
Итак, в зависимости от способа применения процентной ставки i имеем четыре метода наращения суммы долга по этой ставке: по простой (4.3), сложной (4.7), номинальной (4.8), при постоянной интенсивности процентов в единицу времени (или по постоянной силе роста) (4.9).
Экономический смысл процесса дисконтирования денежных потоков состоит в нахождении суммы, эквивалентной будущей стоимости денежных средств. Эквивалентность будущих и текущих денежных сумм означает, что инвестору должно быть безразлично, иметь сегодня некоторую сумму денежных средств или иметь через определенный период времени ту же сумму, но увеличенную на величину начисленных за период процентов. Именно в этом случае временного безразличия можно говорить о том, что найдена текущая стоимость будущих потоков.
Надо обратить внимание на то, что кредитору выгоднее выдавать ссуду под простой дисконт, а не под простой процент. Простой дисконт (d) представляет процентный доход, который вычитается из ссуды в момент ее выдачи. Сравним наращенную сумму, которую надо вернуть кредитору при условии выдачи кредита в одинаковой сумме, но под простой процент — в одном случае и под простой дисконт — в другом.
Поскольку простой процент представляет отношение суммы приращения за какой-то срок к начальной сумме, это есть ставка процента, эффективность вложений, или интерес кредитора (по зарубежной терминологии). Дисконт, или относительная скидка, — это отношение суммы приращения за определенный срок к наращенной сумме.
В практических финансовых расчетах с использованием дисконта удобно применять дисконт-фактор (V) — отношение начальной суммы вложений к наращенной или разность между единицей и дисконтом за определенный срок:
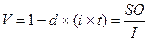
Для расчета суммы, которую клиент получит на руки, если по условиям кредитного договора ссуда выдается под простой дисконт, надо предполагаемую к возврату сумму умножить на величину дисконт-фактора.
При увеличении числа периодов начисления сложных процентов при одной и той же годовой ставке за одно и то же время наращения сумма будет возрастать.
В финансовых расчетах с использованием сложных процентов принято определять эффективную ставку, т.е. такую годовую номинальную ставку сложных процентов, которая дает возможность получить тот же результат, как и при начислении процентов несколько раз в году. Равенство наращенных сумм обеспечивается здесь равенством первоначальных сумм, периодов и множителей наращения.
Эффективная процентная ставка будет больше номинальной. Это видно из соответствующих алгоритмов, где iэф — эффективная ставка. Множители наращения должны быть равны
(1 + iэф)t = (1+im/m)mt
Отсюда эффективная ставка составит
iэф = (1+ im/m)m – 1
В финансовых расчетах должна учитываться инфляция, тем более если она значительна. С одной стороны, сумма, положенная, например, на депозит, получит приращение, а с другой — утратит свою реальную стоимость в результате инфляции. Для определения наращенной суммы с учетом инфляции используют алгоритм
Sинф= S0 * (1 + im/m)t / (1 + h)t
где Sинф — наращенная сумма с учетом инфляции; S0 — базовая сумма; im — годовая номинальная банковская ставка, применяемая m раз в году; h — ожидаемый месячный темп инфляции; t — число месяцев.
Чаще всего финансовые операции имеют продолжительный характер, состоят не из одного разового платежа, а из потоков платежей и нередко с разными знаками. В качестве примера можно привести: ежегодные выплаты процентов по облигациям, ежемесячные взносы на погашение потребительского кредита, получение ежемесячных стипендий от благотворительного фонда; арендные платежи; периодические вклады в банк для образования страхового фонда и др.
В таких финансовых операциях возникает необходимость найти наращенную сумму потока платежей или, наоборот, по наращенной сумме определить величину отдельного платежа. Для целого ряда финансовых расчетов разработаны математические модели.