Концепция риска и доходности в финансовом менеджменте

Риск и доходность в финансовом менеджменте и анализе рассматриваются как две взаимосвязанные категории. Они могут быть ассоциированы как с каким-либо отдельным видом финан­совых активов, так и с их комбинацией (в дальнейшем под активами мы будем подразумевать в основном такие финансовые инструменты, как акции и облигации).

Существуют различные определения понятия «риск». Так, в наиболее общем виде под риском понимают вероятность возник­новения убытков или недополучения доходов по сравнению с прогнозируемым вариантом. Можно сформулировать и более детализированные подходы к определению этого понятия. В частности, риск может быть определен как уровень конкретной финансовой потери, выражающейся:

а) в возможности не достичь поставленной цели;

б) неопределенности прогнозируемого ре­зультата;

в) субъективности оценки прогнозируемого результата.

Риск является весьма сложной и многоаспектной категорией. Не случайно в научной литературе приводятся десятки видов риска (производственный, валютный инвестиционный, экологи­ческий, политический и др.) при этом основным классификацион­ным признаком чаще всего служит объект, рисковость которого пытаются охарактеризовать и проанализировать. В данном слу­чае будем рассматривать риск в отношении финансовых активов; кроме того, позднее будут рассмотрены другие виды риска в отношении деятельности компании в целом и управления инвестиционными проектами.

В приложении к финансовым активам используют следу­ющую интерпретацию риска и его меры: рисковость актива характеризуется степенью вариабельности дохода (или доход­ности), который может быть получен благодаря владению дан­ным активом. Так, государственные ценные бумаги обладают относительно небольшим риском, поскольку вариация дохода по ним в стабильной не подверженной кризисам экономике прак­тически равна нулю. Напротив, обыкновенная акция любой ком­пании представляет собой значительно более рисковый актив, поскольку доход по таким акциям может ощутимо варьировать.

Активы, с которыми ассоциируется относительно больший размер возможных потерь, рассматриваются как более рисковые; вполне естественно, что к таким активам предъявляются и боль­шие требования в отношении доходности.

Доход, обеспечиваемый каким-либо активом, состоит из двух компонент — полученных дивидендов и дохода от изменения стоимости актива. Доход, исчисленный в процентах к первона­чальной стоимости актива, называется доходностью данного актива, или нормой прибыли. Доход — абсолютный показатель, его можно суммировать в пространстве и времени (в данном случае пока не учитывается временная стоимость денег); доходность — показатель относительный, и такого суммирования делать уже нельзя.

Финансовые менеджеры пытаются учитывать риск в своей работе. При этом возможны различные варианты поведения менеджера в зависимости от склонности к риску. Однако клю­чевая идея, которой руководствуется менеджер, заключается в следующем: требуемая (или ожидаемая) доходность и риск изме­няются в одном направлении, т.е. пропорционально друг другу.

Совершенно очевидно, что поскольку риск является вероят­ностной оценкой, его количественное измерение не может быть однозначным и предопределенным. Более того, проблема оценки риска финансовых активов многоаспектна как с позиции методов оценки, так и с позиции стратегии и тактики управления этими активами.

Количественно риск может быть охарактеризован как некий показатель, измеряющий вариабельность дохода или доходно­сти. Таким образом, для этой цели можно использовать ряд статистических коэффициентов, в частности:

· размах вариации,

· дисперсию,

· среднее квадратическое отклонение, называемое иногда стандартным,

· коэффициент вариации.

Рассмотрим ряд статистических величин (это могут быть как абсолютные, так и относительные величины):

.

Размахом вариации называется разность между максимальным и минимальным значениями признака данного ряда:

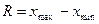
Этот показатель имеет ряд недостатков:

1. он дает грубую оценку степени вариации значений признака;

2. он является абсолютным показателем и потому его применение в сравнитель­ном анализе весьма ограничено;

3. его величина слиш­ком зависит от крайних значений ранжированного ряда.

Формулы расчета показателей дисперсии, среднего квадратичного отклонения, коэффициента вариации были приведены выше.

В отношении оценки риска финансовых активов необходимо сделать три замечания.

1. Во-первых, как отмечалось выше, количе­ственно риск может оцениваться вариабельностью либо дохода, либо доходности. Поскольку доход в абсолютной оценке может существенно варьировать при сравнительном анализе различных финансовых активов, то принято в качестве базисного показа­теля, характеризующего результативность операции с финансо­вым активом, использовать доходность. Очевидно, что, вложив ту или иную сумму денежных средств в акции, можно получать разный доход по абсолютной величине, однако доходность не зависит от размера инвестиции и потому сопоставима в простра­нственно-временном разрезе.

2. Во-вторых, основными показателями оценки риска на рынке капитала являются дисперсия и среднее квадратическое отклоне­ние. Распространенность и пригодность их в сравнительном анализе в данном случае объясняется тем обстоятельством, что базисным показателем при расчетах является доходность, т.е. относительный показатель, сопоставимый как в динамике, так и по различным видам активов. Поэтому независимо от анализи­руемых активов соответствующие им показатели доходности и дисперсии однопорядковые и нет острой необходимости приме­нять в оценке коэффициент вариации.

3. В-третьих, приведенные формулы рассчитаны на дискретные ряды. В приложении к финансовым активам они могут приме­няться в ретроспективном анализе. Однако, как уже неоднократ­но подчеркивалось, при работе на рынке капитала гораздо более ценен перспективный анализ, в рамках которого большинство величин, представляющих интерес для инвестора, оцениваются в вероятностных терминах. Ниже будут приведены соответст­вующие формулы для расчета.

Необходимо отметить еще одну очень важную особенность анализа риска и доходности. Как и любая вероятностная катего­рия, риск может быть оценен по-разному. Однако речь должна идти не только и не столько о различии в алгоритмах и критериях оценки, приведенных выше, сколько о том, рассматривается ли данный финансовый актив изолированно или как составная часть набора активов.

При рассмотрении актива изолированно никаких особых проблем теоретического характера в принципе не возникает, а его рисковость может быть измерена с помощью одной из рассмотренных выше статистик. Тем не менее, как и в любом перспективном анализе, инвестор в этом случае сталкивается с одной проблемой, а именно с проблемой оценки ожидаемых значений исходных параметров. В частности, какой бы мерой инвестор ни пользовался, ему необходимо оценить ожидаемую доходность актива. Чаще всего делают три оценки: пессимисти­ческую (k_p), наиболее вероятную (k_ml) и оптимистическую (k_о). Безусловно, число исходов может быть увеличено, однако степень разумной достоверности ожидаемых значений доход­ности и вероятностей их осуществления при этом, естественно, снизится.

Если ограничиваются тремя оценками, то наиболее общей мерой риска, ассоциируемого с данным активом, может служить размах вариации ожидаемой доходности, рассчитываемый по формуле:

R = k_o - k_p

Из представленных расчетов видно, что оба финансовых ак­тива имеют примерно одинаковую наиболее вероятную доход­ность, однако второй из них может считаться в два раза более рисковым. Отметим, что если бы был выбран какой-то другой критерий оценки риска, его степень могла бы быть другой.

Можно рассчитать и другие меры риска, основанные на по­строении вероятностного распределения значений доходности и исчислении стандартного отклонения от средней доходности и коэффициента вариации, которые и рассматриваются как степень риска, ассоциируемого с данным активом. Таким образом, чем выше коэффициент вариации, тем более рисковым является дан­ный вид актива. Последовательность аналитических процедур в этом случае такова:

· делаются прогнозные оценки значений доходности (k_i) и вероятностей их осуществления (P_i), і = 1,... n, где n — число исходов;

· рассчитывается наиболее вероятная доходность (k_ml) по формуле:

k_ml =

· рассчитывается среднее квадратичное отклонение по формуле:

· рассчитывается коэффициент вариации по формуле:

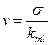
С течением времени риск, ассоциируемый с данным активом, возрастает. Отсюда можно сделать очень важный вывод: чем более долговременным является данный вид актива, тем он более рискован, тем большая вариация доходности с ним связана. Именно поэтому различается до­ходность и рисковость различных финансовых инструментов, например, акций и облигаций: вариация доходности акций может ощутимо варьировать, т.е. этот вид финансового инструмента более рискован.