Лекция 2
Принцип суперпозиции колебаний и границы его применимости (4 часа)
Вопросы:
1. Понятие о связанных осцилляторах
2. Сложение колебаний:
· направленных по одной прямой.
· взаимоперпендикулярных колебаний.
3. Биения.
Понятиео связанных осцилляторах
 Особый интерес представляет случай, когда одна колеблющаяся система связана с другой системой, которая тоже может колебаться- такие системы называются связанными.
Особый интерес представляет случай, когда одна колеблющаяся система связана с другой системой, которая тоже может колебаться- такие системы называются связанными.
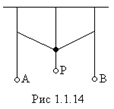
ПРОСТОЙ ПРИМЕР связи – два маятника, соединённые нитью, к середине которой подвешен груз Р (рис.1.1.14).
При помощи силы, действующей на нить, маятник А связан с маятником В. Если маятник В во время колебания удалится от А, то сила связи между этими маятниками становится больше, а при сближении – меньше. Маятник А получает в такт с колебаниями маятника В импульс периодически действующей силы, частота которой согласуется с частотой собственных колебаний А, но может отличаться от частоты колебаний В.
Под влиянием силы связи между маятниками разной длины маятник А приходит в колебательное движение. Когда маятник В колеблется, его амплитуда возрастает с каждым новым импульсом, в то время, как амплитуда В убывает. Спустя известное время, амплитуды маятника А убывают, а маятника В возрастают до тех пор, пока не наступит обратное явление. Таким образом, энергия колебаний передаётся через связь от одной колеблющейся системы другой и обратно.
Если периоды собственных колебаний обоих маятников равны, то обмен энергией осуществляется нацело.
Из эксперимента известно, что процесс передачи энергии между маятниками идёт тем быстрее, чем больше масса груза Р. Если два маятника колеблются с одинаковыми периодами, амплитудами и фазами колебаний, то никакого обмена энергией между ними не происходит. Должна быть разница в амплитудах или фазах колебаний, чтобы энергия была получена или отдана.
 2. Сложение колебаний
2. Сложение колебаний
Под сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах.
Различают два предельных случая:
Сложение колебаний:
· направленных по одной прямой.
· взаимно перпендикулярных колебаний
Сложение одинаково направленных колебаний можно производить методом векторных диаграмм:
Любое гармоническое колебание можно представить в виде вектора следующим образом.
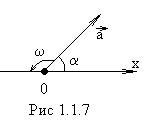
1. Выберем ось х с началом отсчета в точке О (рис.1.1.7)
Построим из точки О вектор  , который составляет угол
, который составляет угол  с осью х.
с осью х.
Пусть этот вектор поворачивается с угловой скоростью  .
.
Проекция вектора  на ось Х равна:
на ось Х равна: 
то есть она совершает гармонические колебания с амплитудой а.
2. Рассмотрим два гармонических колебания одинакового направления и одинаковой циклической малой  , заданные векторами
, заданные векторами 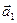 и
и  .
.
 Смещения по оси Х равны:
Смещения по оси Х равны:


результирующий вектор  имеет проекцию
имеет проекцию  и представляет собой результирующее колебание (рис.1.1.8),
и представляет собой результирующее колебание (рис.1.1.8),
по теореме косинусов 
Таким образом, сложение гармонических колебаний производится сложением векторов.
3.  Проведем сложение взаимно перпендикулярных колебаний.
Проведем сложение взаимно перпендикулярных колебаний.
Пусть материальная точка совершает два взаимно перпендикулярных колебания частотой  :
:

 .
.
Сама материальная точка при этом будет двигаться по некоторой криволинейной траектории.
Из уравнения движения следует:  ,тогда
,тогда
 . (1.1.9)
. (1.1.9)
Из уравнения (1.1.9) можно получить уравнение эллипса (рис.1.1.9):
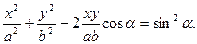
4. Рассмотрим частные случаи этого уравнения:
·  Разность фаз колебанийα = 0.
Разность фаз колебанийα = 0.
При этом  т.е.
т.е. 
или  - э то уравнение прямой, и результирующее колебание происходит вдоль этой прямой с амплитудой
- э то уравнение прямой, и результирующее колебание происходит вдоль этой прямой с амплитудой  (рис.1.1.10).
(рис.1.1.10).
· Если разность фаз  то уравнение (1.1.9) переходит в уравнение эллипса, приведенного к координатным осям,
то уравнение (1.1.9) переходит в уравнение эллипса, приведенного к координатным осям, 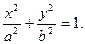
 При
При  материальная точка движется по окружности, уравнение которой
материальная точка движется по окружности, уравнение которой  (рис.1.1.11).
(рис.1.1.11).
·  Если частоты колебаний неодинаковы, то материальная точка описывает фигуры Лиссажу (рис.1112).
Если частоты колебаний неодинаковы, то материальная точка описывает фигуры Лиссажу (рис.1112).
БИЕНИЯ
Негармонические колебания, получающиеся в результате наложения двух одинаково направленных гармонических колебаний с близкими частотами 
 наз. Биениями.
наз. Биениями.
Рассмотрим сложение колебаний одного направления, частоты которых мало отличаются друг от друга. В этом случае результирующее движение можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такие колебания называются биениями.
Пусть частота одного колебания  , второго
, второго 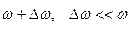 .
.
Амплитуды обоих колебаний одинаковы и равны а.
Начальные фазы равны нулю.
В таком случае уравнения колебаний имеют вид: 
Сложим эти выражения:
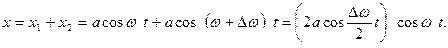 (1.1.10)
(1.1.10)
 График функции х(t) представлен на рис. 1.1.13.
График функции х(t) представлен на рис. 1.1.13.
Множитель  меняется гораздо медленнее, чем
меняется гораздо медленнее, чем  , поэтому (1.1.10) можно рассматривать как гармоническое колебание частоты
, поэтому (1.1.10) можно рассматривать как гармоническое колебание частоты  , амплитуда которого меняется по некоторому периодическому закону
, амплитуда которого меняется по некоторому периодическому закону

Переменную величину  условно называют амплитудой биений. Эта величина:
условно называют амплитудой биений. Эта величина:
- характеризует размах колебаний при биениях,
- изменяется в пределах 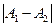 до
до 
 с циклической частотой Ω.
с циклической частотой Ω.
Частота изменения амплитуды – частота биений – равна разности частот складываемых колебаний  :
:
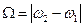 - циклическая частота биений.
- циклическая частота биений.
Период биений и частота биений равны

 ,
,
Где Т1, ν1 и Т2, ν2 – периоды и частоты складываемых колебаний.