ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 15
Тема: Решение задач на применения формулы Бернулли
Краткие теоретические сведения
Если вероятность p наступления события A в каждом испытании постоянна, то вероятность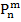 
того, что в n независимых испытаниях событие A наступит m раз, находится по формуле Бернулли:
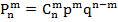
(где q = 1 – p - вероятность того, что событие не наступит).
Пример 1. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:
а) три элемента;
б) не менее четырех элементов.
Решение: Имеем схему Бернулли с параметрами p=0,2 (вероятность того, что элемент откажет), n=5 (число испытаний, то есть число элементов), k (число «успехов», отказавших элементов). Будем использовать формулу Бернулли (вероятность того, что для n элементов отказ произойдет в k элементах):
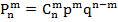
Получаем
а) Вероятность того, что откажут ровно три элемента из пяти:
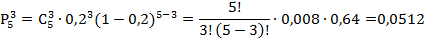
б) Вероятность того, что откажут не менее четырех элементов из пяти (то есть или четыре, или пять):
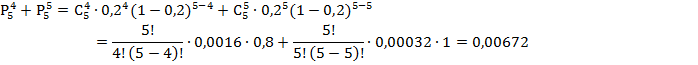
Пример 2. Найти вероятность того, что при 10 бросках монеты орёл выпадет 3 раза.
Решение: сначала немного порассуждаем: всего проводится 10 повторных независимых испытаний. Сколькими способами можно выбрать 3 испытания, в которых выпадет орёл?
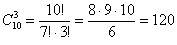способами!
Это что же получается – записывать 120 слагаемых, в каждом из которых 10 множителей? =)
Используем формулу Бернулли: 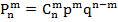, в данном случае:
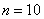– всего испытаний;
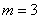– количество испытаний, в которых должен появиться орёл;
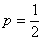– вероятность появления орла в каждом испытании;
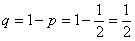– вероятность появления решки в каждом испытании.
Таким образом:
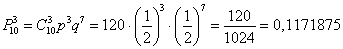– вероятность того, что при 10 бросках монеты орёл выпадет ровно 3 раза.
|
|
Ответ: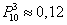 
Пример 3. Производится 8 выстрелов по цели, в каждом из которых вероятность попадания равна 0,1. Найти вероятность того, что цель будет поражена хотя бы два раза.
Решение: используем формулу Бернулли: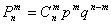 
, в данном случае:
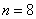– всего выстрелов;
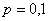– вероятность попадания в цель при каждом выстреле;
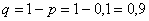– вероятность промаха при каждом выстреле.
По теореме сложения вероятностей несовместных событий:
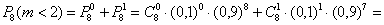
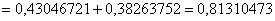– вероятность того, что в серии из 8 выстрелов будет ни одного или 1 попадание.
Найдём вероятность противоположного события:
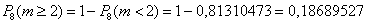– вероятность того, что цель будет поражена хотя бы два раза.
Ответ: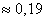 
Содержание работы
Вариант 1
Задание 1. Устройство, состоящее из шести независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,3. Найти вероятность того, что откажут:
а) четыре элемента;
б) не менее пяти элементов.
Задание 2. Найти вероятность того, что при 8 бросках монеты орёл выпадет 2 раза.
Задание 3. Производится 10 выстрелов по цели, в каждом из которых вероятность попадания равна 0,3. Найти вероятность того, что цель будет поражена хотя бы три раза.
Вариант 2
Задание 1. Устройство, состоящее из семи независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,1. Найти вероятность того, что откажут:
а) пять элементов;
б) не менее шести элементов.
Задание 2. Найти вероятность того, что при 9 бросках монеты орёл выпадет 4 раза.
Задание 3. Производится 6 выстрелов по цели, в каждом из которых вероятность попадания равна 0,05. Найти вероятность того, что цель будет поражена хотя бы два раза.
|
|