https://studopedia.su/9_74976_nagruzka-linii-razlichnimi-soprotivleniyami.html
СТОЯЧИЕ ВОЛНЫВ ЛИНИЯХ
Режим бегущей волны получается в линии только в случае, если она нагружена на активное сопротивление, равное волновому. При ином значении нагрузочного сопротивления в линии получается более сложный процесс. Рассмотрим случай, когда линия разомкнута на конце, т. е. когда нагрузочное сопротивление бесконечно велико. Так как в конце разомкнутой линии нет нагрузочного сопротивления, энергия бегущей волны не может быть поглощена в конце линии, но волна не может и продолжать удаляться от генератора, потому что линия обрывается. Бегущая волна, дойдя до конца разомкнутой линии, отражается и двигается обратно к генератору. Таким образом, в линии распространяются две бегущие волны: одна — падающая — движется от генератора к концу линии, а другая — отраженная — движется в обратном направлении.
Физически процесс отражения можно объяснить следующим образом. Когда падающая волна доходит до конца линии, то там начинают накапливаться заряды, а следовательно, возникает дополнительная разность потенциалов. Она действует подобно напряжению некоторого генератора и возбуждает в линии новую бегущую волну, движущуюся от конца линии к ее началу, т. е. отраженную волну.
Пренебрегая потерями в линии, можно считать, что энергия отраженной волны равна энергии падающей волны. В результате сложения двух волн, имеющих одинаковые амплитуды и движущихся навстречу друг другу, возникают так называемые стоячие волны, которые резко отличаются от бегущих волн.
На рис.1 показано сложение падающей и отраженной волн напряжения для некоторого момента времени. Для примера взят момент, когда амплитуда падающей волны находится на расстоянии 1/8*? от конца линии.
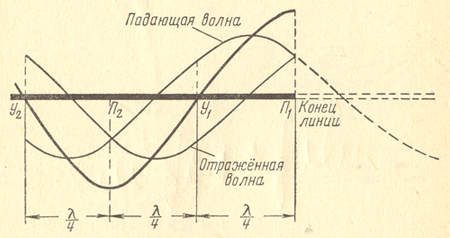
Рис.1 — Сложение падающей и отраженных волн
Штрихом изображено продолжение падающей волны, которое существовало бы, если бы линия не обрывалась. Если эту штриховую синусоиду перегнуть на 180° вокруг вертикальной оси, проходящей через конец линии, т. е. нарисовать в обратную сторону, то она будет изображать отраженную волну. Отраженная волна является продолжением падающей волны, но только движется от конца линии к генератору. Суммарное напряжение падающей и отраженной волн показано жирной линией. Оно имеет наибольшее значение в точках П1 и П2 (на конце линии и на расстоянии 1/2*? от конца). В точках У1 и У2 на расстояниях 1/4*? и 3/4*? от конца линии это напряжение равно нулю.
В любой другой момент падающая и отраженная волны складываются так, что в точках П1 и П2 напряжение будет наибольшее, а в точках У1 и У 2 — равно нулю. Например, через одну восьмую периода падающая волна сдвинется вправо на 1/8*? и в точке У1 будет ее нулевая фаза, а отраженная волна сдвинется на 1/8*? влево и в точку У1 придет ее нулевая фаза. Ясно, что в точке У1 суммарное напряжение опять равно нулю, а в точках П1 и П2 напряжение будет наибольшее и равно двойной амплитуде бегущей волны.
Точки У1 и У2, в которых напряжение всегда равно нулю, называются узлами напряжения, а точки наибольшего напряжения П1 и П2 называются пучностями. Узлы и пучности остаются в одних и тех же точках линии, и вся суммарная волна «стоит на месте». Поэтому ее и назвали стоячей волной.
Стоячую волну можно получить на опыте с веревкой, если один ее конец непрерывно качать и посылать к закрепленному концу бегущие волны, которые будут отражаться от места крепления.
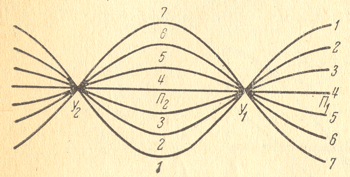
Рис.2 — Распределение напряжения вдоль линии при стоячей волне для разных моментов вемени
Характер распределения напряжения вдоль линии при стоячей волне не изменяется с течением времени. В разные моменты времени изменяется только величина напряжения в каждой точке линии. На рис.2 показано распределение напряжения вдоль разомкнутой линии для нескольких различных моментов времени на протяжении одного полупериода. Кривая 1 соответствует фазе, когда напряжение в линии наибольшее. Далее напряжение становится меньше (кривые 2 и 3). Через четверть периода (прямая 4) напряжение во всей линии равно нулю. Затем оно меняет знак и возрастает (кривые 5 и 6). Через пол периода после начала процесса напряжение снова достигает амплитудного значения (кривая 7), но с обратным знаком. В каждой точке линии напряжение колеблется по синусоидальному закону, причем амплитуда этого колебания для разных точек различна. Для пучностей амплитуда наибольшая, равный двойной амплитуде бегущей волны, для других точек она меньше, и, наконец, для узлов она равна нулю.
Все сказанное относится и к току. Но отраженная волна тока движется от конца линии с противоположной фазой. Действительно, электроны, дойдя до конца линии, дальше не могут перемещаться и двигаются обратно. Это означает, что ток изменяет знак. В результате на конце линии суммарный ток равен нулю, т. е. получается узел тока.
Таким образом, в стоячей волне узлы тока получаются там, где пучности напряжения, а пучности тока находятся в узлах напряжения. Иначе говоря, стоячая волна тока сдвинута на 1/4*? относительно стоячей волны напряжения. Графически это изображено на рис.3 двумя кривыми. Кривая тока дана сплошной линией, а кривая напряжения — штрихом.
Амплитуда напряжения в пучности Uпуч, равная двойной амплитуде напряжения бегущей волны 2Um, пропорциональна амплитуде тока в пучности Iпуч, которая равна двойному значению амплитуды тока бегущей волны 2Im. Отношение этих величин есть волновое сопротивление Zo:
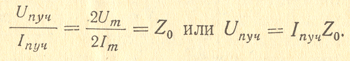
Мощность стоячей волны является реактивной, так как энергия не расходуется (линию мы считаем идеальной). Действительно, как уже говорилось, во времени ток и напряжение имеют сдвиг фаз на.четверть периода, т. е. на 90°. Если в какой-то момент в линии напряжение имеет амплитудное значение, то в это время ток везде равен нулю. Через четверть периода напряжение по всей линии уменьшится до нуля, а ток дойдет до амплитудного значения.
Кривые рис. 3 показывают обычно распределение тока и напряжения для амплитудных значений и, следовательно, по времени отличаются друг от друга на 1/4*Т. Нет смысла показывать кривые для других моментов времени, так как пучности и узлы не сдвигаются. Даже если изображена только одна кривая, например для тока, то по ней можно судить и о распределении напряжения вдоль линии.

Рис.3 — Изображение стоячих волн тока и напряжения в линии
Сдвиг фаз на 90° между током и напряжением при стоячей волне показывает, что в линии происходит колебание энергии, сходное с колебательным процессом в замкнутом контуре. Когда напряжение в линии наибольшее, а ток равен нулю, то вся энергия сосредоточена в электрическом поле. Через четверть периода напряжение равно нулю, а ток имеет наибольшее значение и вся энергия сосредоточена в магнитном поле. Еще через четверть периода энергия снова возвратится в электрическое поле и процесс колебания энергии повторится.
Выясним теперь процессы в разомкнутой линии при различном соотношении между ее длиной и длиной волны питающего генератора. Для определенности примем, что внутреннее сопротивление генератора значительно меньше волнового сопротивления линии. На рис.4 показано распределение тока и напряжения для характерных случаев работы линии и приведены для них эквивалентные схемы (с целью упрощения кривые тока и напряжения показаны только для одного провода).
Как известно, на конце разомкнутой линии всегда получаются пучность напряжения и узел тока. На входе линии ток и напряжение могут иметь различные значения в зависимости от длины линии. Входное сопротивление также изменяется в широких пределах, так как оно всегда равно отношению напряжения к току в начале линии. При этом во всех случаях, когда входное сопротивление линии значительно больше внутреннего сопротивления генератора, можно считать, что напряжение на зажимах генератора равно его эдс.
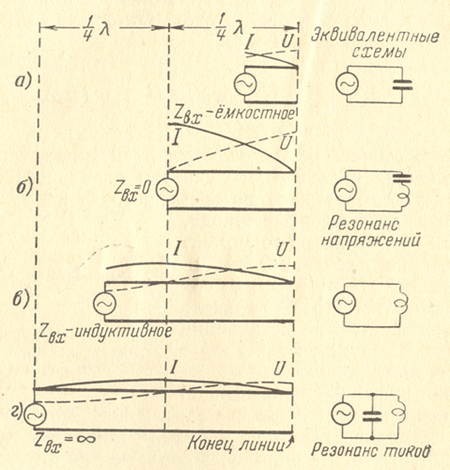
Рис.4 — Стоячие волны в разомкнутой линии различной длины
Когда длина линии L меньше четверти длины волны (рис.4 а), то в начале линии ток и напряжение имеют некоторые значения и сдвинуты по фазе на 90°. Следовательно, входное сопротивление в этом случае является реактивным. Оказывается, что оно имеет емкостный характер. Действительно, два коротких провода, подключенных к генератору, представляют собой конденсатор. И чем короче линия, тем меньше емкость этого конденсатора, т. е. тем больше емкостное входное сопротивление. Генератор в этом случае нагружен на некоторую емкость, что и показано на эквивалентной схеме справа. Вследствие большой величины входного сопротивления ток в линии получается малым, а напряжение в линии превышает напряжение генератора.
Если приближать длину линии к 1/4*?, то напряжение в начале линии становится меньше по сравнению с его значением в пучности, а ток увеличивается и входное сопротивление уменьшается. Когда L = 1/4*? (рис.4 б), то в начале будут узел напряжения и пучность тока. Тогда Zвх = U/I = 0, и для генератора получается режим короткого замыкания.
В этом случае напряжение в линии, пропорциональное току, достигает наибольшего значения, т. е. наблюдается явление резонанса напряжений. Таким образом, четвертьволновая разомкнутая линия эквивалентна последовательному резонансному контуру. Как известно, такой контур имеет при резонансе наименьшее и чисто активное сопротивление. Поэтому ток и напряжение в нем при резонансе достигают наибольших значений.
Идеальный контур имеет при резонансе входное сопротивление, равное нулю, подобно идеальной линии. При изменении длины линии в ту или другую сторону от 1/4*? ее входное сопротивление увеличивается и становится емкостным или индуктивным. Именно так меняется при расстройке и сопротивление последовательного контура.
В реальной линии имеются потери энергии и Zвх при резонансе неточно равно нулю. Обращается в нуль только реактивное входное сопротивление, a Zвх становится наименьшим и чисто активным, так как оно обусловлено наличием потерь.
Пусть теперь длина линии больше 1/4*?, но меньше 1/2*?. Тогда напряжение в начале линии уже не равно нулю. Входное сопротивление возрастет и примет индуктивный характер (рис. 4 в). При этом ток и напряжение получаются значительно меньше, чем в четвертьволновой линии, подобно тому, как уменьшается ток и напряжение при расстройке контура.
По мере приближения L к 1/2*? входное сопротивление увеличивается. Когда L= 1/2*? (рис.4 г), то напряжение в начале линии принимает наибольшее значение, равное эдс генератора, а ток становится равным нулю. Следовательно, входное сопротивление должно быть бесконечно велико. В действительности, вследствие наличия потерь в линии, входное сопротивление не равно бесконечности, а принимает некоторое наибольшее значение и является чисто активным.
Получается резонанс, подобный резонансу токов в параллельном контуре. В данном случае полуволновая линия эквивалентна параллельному резонансному контуру потому, что ее входное сопротивление при изменении Длины в ту или другую сторону от 1/2*? уменьшается и приобретает -емкостный или индуктивный характер. Такое же изменение сопротивления при расстройке свойственно и параллельному контуру.
Изменяя дальше L в пределах от 1/2*? до? и воооще при удлинении линии на целое число полуволн, можно получить повторение всех рассмотренных режимов и значений Zвх.
Все рассмотренные случаи можно получить и при постоянной длине линии, изменяя длину волны генератора?. Тогда последовательный резонанс получится в случаях, когда вдоль линии укладывается нечетное число четвертей волны (1/4(*?, 3/4*?, 5/4*? и т д.) — Иначе говоря, кроме резонанса на основной волне, соответствующей L= 1/4*?, будет наблюдаться резонанс на любой нечетной гармонике. Параллельный же резонанс в линии получится не только на основной волне, когда L = 1/2*?, но и на любых как четных, так и нечетных гармониках, когда вдоль линии укладывается целое число полуволн (1/2*?,?, 3/2*? и т. д.). Линия как колебательная система способна резонировать на многих волнах. Этим она отличается от простого колебательного контура, имеющего только одну резонансную частоту.
Свойство резонировать не только на основной собственной частоте, но и на гармониках характерно для всех колебательных систем с распределенными параметрами. Например у струны, имеющей массу и упругость, распределенные по всей ее длине, легко возбудить колебания на гармониках, но это невозможно у маятника.
Следует обратить внимание на то, что при длине линии, равной 1/2*? или целому числу полуволн, входное сопротивление получается таким же, как и сопротивление на конце лини(в данном случае бесконечно большое). А при длине линии, равной 1/4*?. или нечетному числу четвертей волны, входное сопротивление равно нулю, т. е. имеет величину, обратную сопротивлению на конце линии (0= 1/?. Такое влияние длины линии на величину входного сопротивления наблюдается и при любых других значениях нагрузочного сопротивления R длиной в целое число полуволн не изменяет величину сопротивления и у нее всегда Zвх=R, а линия длиной, равной нечетному числу четвертей волны, преобразовывает большое нагрузочное сопротивление в малое входное и наоборот.
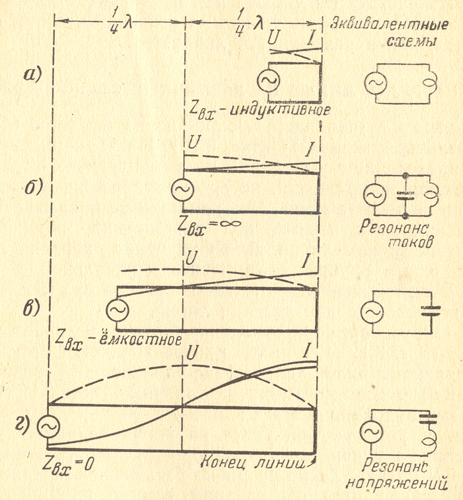
Рис.5 — Стоячие волны в короткозамкнутой линии различной длины
В режиме стоячих волн работает также короткое замкнутая линия (ряс.5), у которой на конце нагрузочное сопротивление равно нулю (R = 0). Поглощение энергии в таком сопротивлении отсутствует, и падающая волна полностью отражается. Поэтому возникают стоячие волны, как и в разомкнутой линии. Разница заключается в том, что распределение тока и напряжения в короткозамкнутой линии сдвинуто на четверть волны по сравнению с разомкнутой линией.
На конце линии напряжение равно нулю, т. е. там находится узел напряжения, так как R = 0 (короткое замыкание). Но у стоячей волны узлы напряжения совпадают с пучностями тока и наоборот. Значит, на конце короткозамкнутой линии получается пучность тока.
Действительно, ведь там, где имеется короткое замыкание, ток всегда бывает наибольшим. У разомкнутой линии, наоборот, на конце были пучность напряжения и узел тока. Зная, что получается на конце линии, нетрудно начертить кривые распределения тока и напряжения для различных соотношений между длиной линии и длиной волны генератора.
Эти кривые даны на рис.5 для идеальной линии, у которой волновое сопротивление значительно больше внутреннего сопротивления генератора. Они показывают, что короткозамкнутая линия по своим свойствам противоположна разомкнутой.
При L<1/4*? входное сопротивление имеет индуктивный характер (рис.5 а). В этом случае линию можно представить как прямоугольный виток, обладающий некоторой индуктивностью. Если L = 1/4*?, то Zвх =? и, следовательно, короткозамкнутая четвертьволновая линия эквивалентна параллельному резонансному контуру (рис.5 б).
Когда 1/4*? < L < 1/2*?, то входное сопротивление имеет емкостный характер (рис.5 в). Наконец, при L=1/2*? входное сопротивление равно нулю и линия эквивалентна последовательному резонансному контуру (рис.5 г).
При дальнейшем увеличении длины линии все повторяется. Если изменять частоту генератора при неизменной длине линии, то получается резонанс не только на основной частоте, но и на гармониках, как в разомкнутой линии.
https://www.radioingener.ru/stoyachie-volny-v-liniyax/
Узлы стоячей волны
Стоячие волны
Волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Уравнение стоячей волны
Складываем волны
и
S=
(учли, что k = 2π/λ)— уравнение стоячей волны.
Пучности стоячей волны
Точки, в которых амплитуда максимальна (Aст = 2Аcos(2πx/λ)). Это точки среды, для которых
2πx/λ= (m=0,1,2,….)
Координаты пучностей
(m = 0,1, 2,:..).
Узлы стоячей волны
Точки, в которых амплитуда колебаний равна нулю (Aст = 0). Это точки среды, для которых
(m = 0,1, 2,:..).
Координаты узлов
(m = 0,1, 2,...).
Расстояния пучность—пучность и узел—узел равны λ/2, а расстояние пучность—узел равно λ /4.
Образование стоячих волн наблюдают при
интерференции бегущей и отраженной волн. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае получается узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения получается пучность, если более плотная — узел. Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний противоположных направлений, в результате чего получается узел. Если волна отражается от менее плотной среды, то изменения фазы не происходит, и у границы колебания складываются с одинаковыми фазами — получается пучность.
Уравнение стоячей волны и его анализ
Частным случаем интерференции волн, являются стоячие волны.
Стоячей волной называется волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечных волн еще и одинаковую поляризацию.
Поперечная стоячая волна образуется, например, на натянутой упругой нити, один конец которой закреплен, а другой приводится в колебательное движение.
При наложении двух когерентных бегущих плоских волн вида
и где α-разность фаз волн в точках плоскости x=0, образуется плоская синусоидальная стоячая волна, описываемая уравнением
Амплитуда стоячей волны в отличие от амплитуды бегущих волн является периодической функцией координаты x.
Аст.=2А[cos*(k*x+α/2)]
Точки,в которых амплитуда стоячей волны равна 0, называются узлами, а точки где амплитуда двойная –пучности.
Положение узлов и пучностей находится из условий
k*x+α/2=(2m+1)π/2 (узлы)
k*x+α/2=m*n (пучности),где m=0,1,2…
Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины волны λ бегущих волн.
В бегущей волне фаза колебаний зависит от координаты x рассматриваемой точки. В стоячей волне все точки между двумя узлами колеблются с различными амплитудами, но с одинаковыми фазами (синфазно), так как аргумент синуса в уравнении стоячей волны не зависит от координаты x. При переходе через узел фаза колебаний изменяется скачком на π,так как при этом cos(k*x+α/2) изменяет свой знак на противоположный.
https://mydocx.ru/1-56427.html