Приближение функций
Выполнил:
Группа А-352
Проверила:
Анисимов В.А
Санкт-Петербург
2016
Краткие теоретические сведения.
Задача вычисления приближенных значений функции при любом значении аргумента на основе имеющихся табличных данных решается путем приближенной замены функции 
более простой функцией 
, которую нетрудно вычислять при любом значении аргумента x в заданном интервале его изменения.
Приближение функции более простой функцией называется аппроксимацией (от латинского approximo – приближаюсь). Аппроксимирующую функцию строят таким образом, чтобы отклонения (в некотором смысле) от в заданной области было наименьшим.
Алгоритм исследования:
1.Выбор класса функции
- многочлены
-тригонометрические функции
-логарифмы, экспоненты и так далее.
2. Критерии близости функции
- точка в узлах –интерполяция
- приближение в узлах – аппроксимация
3. Правило получения значений между узлами.
Приближение функции более простой функцией называется аппроксимацией (от латинского approximo – приближаюсь). Аппроксимирующую функцию строят таким образом, чтобы отклонения (в некотором смысле) от в заданной области было наименьшим.
Непрерывная аппроксимация. Если исходная функция 
задана аналитическим выражением, то при построении аппроксимирующей функции возможно требовать минимальности отклонения одной функции от другой на некотором непрерывном множестве точек, например, на отрезке 
. Такой вид аппроксимации называется непрерывным или интегральным.
Теоретически для наилучшего приближения целесообразно требовать, чтобы во всех точках некоторого отрезка отклонения аппроксимирующей функции от функции было по абсолютной величине меньше заданной величины 
:
, 
.
В этом случае говорят, что функция равномерно приближает функцию с точностью e на интервале . Практическое получение равномерногоприближение представляет большие трудности, и поэтому этот способ применяется главным образом в теоретических исследованиях.
Наиболее употребительным является так называемое среднеквадратичное приближение, для которого наименьшее значение имеет величина
.
Потребовав обращения в нуль частных производных от М по параметрам, определяющим функцию , получают уравнения, позволяющие найти наилучшие значения этих параметров.
Точечная аппроксимация. Аппроксимация, при которой приближение строится на заданном дискретном множестве точек 
, называется точечной.
Для получения точечного среднеквадратичного приближения функции 
, заданной таблично, аппроксимирующую функцию строят из условия минимума величины
,
где 
– значения функции в точках 
.
Основная сфера применения среднеквадратичного приближения – обработка экспериментальных данных (построение эмпирических формул) 
.
Метод наименьших квадратов. Будем считать, что вид эмпирической формулы выбран, и ее можно представить следующим образом
, (4.22)
где 
– известная функция, 
– неизвестные параметры. Задача состоит в том, чтобы определить такие значения параметров, при которых эмпирическая формула дает хорошее приближение данной функции, значения которой в точках равны (
).
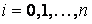Значения могут отличаться (отклоняться) друг от друга на величину
, 
. (4.23)
Задача нахождения наилучших значений параметров сводится к минимизации отклонений 
.
Один из способов решения этой задачи – среднеквадратичное приближение, суть которого состоит в следующем. Составим сумму квадратов отклонений для всех табличных точек:
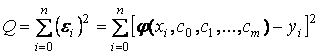. (4.24)
Параметры эмпирической формулы (4.22) будем определять из условия минимума функции 
. В этом состоит метод наименьших квадратов (МНК).
Поскольку неизвестные параметры выступают здесь в роли независимых переменных функции Q, то ее минимум (экстремум) найдем, приравнивая нулю частные производные по этим переменным:
, (4.25)
или с учетом (4.24)
, (4.26)
где 
– значение частной производной от функции по параметру 
в точке .
Соотношения (4.26) – система линейных алгебраических уравнений для определения параметров .
Матричный метод.
Есть система уравнений вида A*X=B, где А – матрица коэффициентов при xi, X- матрица неизвестных xi, B – матрица суммы (xi)n*yi
Умножим данное уравнение на A-1.
Так как A*A-1=1, то получим X=B*A-1 – решение системы уравнений.
Линейная аппроксимация. Частный случай. Рассмотрим применение метода наименьших квадратов для определения коэффициентов линейной функции:
.
Уравнения (4.26) в данном случае будут иметь простой вид
или
. (4.27)
Разделив все слагаемые в уравнениях (4.27) на 
получим
, (4.28)
где введены следующие обозначения
, 
,
, 
.
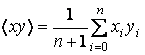Решая систему уравнений (4.28) найдем формулы для коэффициентов а и b линейного уравнения:
, (4.29)
. (4.30)
Аппроксимация 1го порядка
Аппроксимация 2го порядка
Аппроксимация 3го порядка
Вывод: приближенная функция почти соответствует реальной и способна дать оценку и описание первоначальной функции, помочь в ее исследовании.