Сравнение эффективности методов одномерной минимизации

Оптимизация

; Y= ; X- входные, Y-выходные параметры

- cвёртывание векторного критерия

Целевые функции (ЦФ)

 

Однопараметрические Многопараметрические:

-мультипликативная

-аддитивная

Условия работоспособности:

(большее значение соответствует лучшему результату)

(меньшее значение соответствует лучшему результату)

∆ (тип «равенство»)

Мультипликативная ЦФ

Аддитивная ЦФ

;

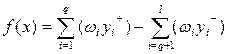Где - вес, . Чем ближе 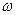к единице, тем соответствующий ей параметр важнее для решения задачи.

Если в задаче все 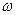, за исключением одной, равны нулю, то вес оставшегося параметра равен 1, и целевая функция обращается в однопараметрическую.

Чаще всего, оптимальное решение есть (min) и задаётся парой чисел: 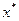и .

 

Графическое представление ЦФ

 

ЦФ однопараметрическая

Локальный минимум:

x*- точка локального минимума, если в выполняется f(x)>f(x*) . (f(x) f(x*)- нестрогий локальный минимум. (x*(1) и x*(2))

Глобальный минимум:

x*- точка глобального минимума, если . (x*(3))

 

Задача оптимизации без ограничений: .

Ограничения существуют: .

.

 

ЦФ зависит от двух параметров f(x1,x2)

Проводятся несколько плоскостей, параллельных , расстояние между ближайшими такими плоскостями одинаково. В самой внутренней изолинии находится либо max, либо min.

 

ЦФ типа «фокус»

 

Решение оптимизационных задач.

Аналитическое Численное Экспериментальное

 

Численное включает в себя:

- локализацию отрезка, внутри которого находится единственный минимум;

- запуск процедуры численного решения.

 

Сравниваем :

 

Если , тогда на следующей итерации:

Если , тогда на следующей итерации: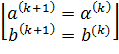

Итерационный процесс идет до момента , где - это заданный критерий окончания счета. Любой x, оказавшийся внутри () будет решением. Например, в качестве приближения можно взять , где 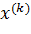- это приближение к точке минимума, полученное на k-ой итерации.

Методы одномерной оптимизации:

1. Дихотомии

2. «Золотого сечения»

3. Чисел Фибоначчи

4. Парабол

Метод дихотомии

 

Количество итераций зависит от:

- длины ab;

- заданной погрешности.

;

 

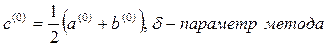
1) ;

2) ;

Счёт продолжается, пока не выполнится .

Решением может являться любая точка . Чаще всего в качестве решения принимают .

k=0
k=1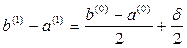
k=2
k

точнее величины отрезок локализации сузить невозможно. Необходимо задавать .

Метод прост в реализации, но неэкономичный и неточный.

Метод «золотого сечения»

«Золотое сечение» [a,b] образуется парой симметрично расположенных относительно центра точек 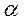и , которые вычисляются:

 

 

 

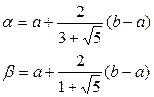
Cвойства:

«золотое сечение» [a; b] и [a; ]

- «золотое сечение» [a,b] и [ ; b]

 

Данный метод более:

- экономичный: со второй итерации функция вычисляется один раз;

- точный;

- обладает более высокой сходимостью.

 

Оценка погрешности:

априорная погрешность. Если добавить условие , то можно узнать необходимое количество итераций. Тогда оставшиеся внутри последнего отрезка значения и принимаются за решение.

 

 

Свойства числа :

 

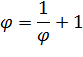
Метод чисел Фибоначчи

Числа Фибоначчи образуются по правилу: каждое следующее есть сумма двух предыдущих. Именно:

№ числа

...

Число Фибоначчи

...

Ряд чисел Фибоначчи формирует золотое сечение:

Метод обеспечивает максимально гарантированное сокращение отрезка локализации при заданном числе N- вычисления функции. При этом количество итераций определяется из формулы:

( )

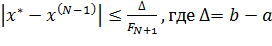Пример:

Пусть . Тогда , откуда , далее по таблице: N+1=11. Т.е. N=10.

Внутренние точки в данном методе ищутся по формулам:

 

Сравнение эффективности методов одномерной минимизации

 

Метод	Длина отрезка локализации	Гарантированная оценка погрешности
Оптимальный пассивный поиск
Метод деления отрезка пополам (N-четное, величиной пренебрегаем)
Метод Фибоначчи
Метод Золотого сечения
N – количество итераций - начальный отрезок локализации

 

Оценим количество вычислений функции, необходимое для достижения точности . Предположим, что .

	Число N при заданном
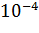
Оптимальный пассивный поиск
Метод деления отрезка пополам ()
Метод Фибоначчи
Метод Золотого сечения

Достижимая точность: , где - радиус интервала неопределенности. Поэтому на шестиразрядном десятичном компьютере недостижима . (Последние 2 столбика справочные)