Сначала рассмотрим примеры, где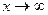 
. Методы решения для последовательности (
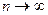) и для функции при 
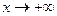во многом очень похожи: для последовательности величина дискретно увеличивается, для функции - непрерывно, но всё равно и там, и здесь неограниченное возрастание.
Задача 181. Найти предел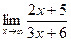 
.
Решение. Так как переменная неграниченно возрастает, то тоже влияют её старшие степени и коэффициенты перед ними.
Сократим дробь: =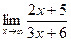 
= 
= 
= 
.
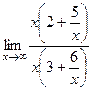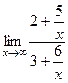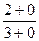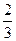Ответ. .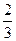
Задача 182. Найти предел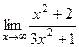 
.
Решение. Аналогично тому, как в прошлом примере, сократим на старшую степень, здесь это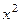 
.
= 
= 
= 
= 
.
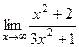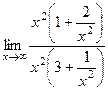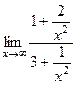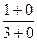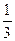Ответ. .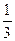
Задача 183. Найти предел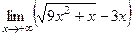 
.
Решение. В этом примере надо домножить и поделить на «сопряжённое» то есть на сумму, чтобы использовать формулу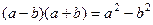 
.
= 
= 
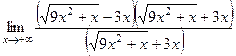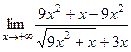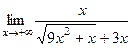теперь сократим на 
: 
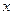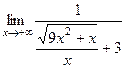
В знаменателе можно представить 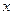в виде 
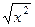, чтобы упростить выражение в знаменателе:
= 
= 
= 
= 
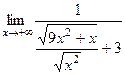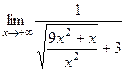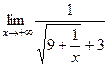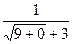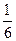. Ответ. .
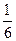Задача 184. Найти предел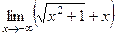 
.
Решение. Заметим, что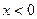 
, то есть указанная сумма, фактически, есть разность. Домножаем на сопряжённое выражение, которое формально будет разностью, а на самом деле - суммой:
= 
=
= 
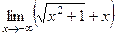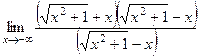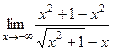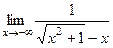. Здесь в знаменателе разность, но 2-я величина отрицательна, то есть фактически - сумма бесконечно-больших. Тогда получается, что дробь - величина, обратная к бесконечно-большой, т.е. бесконечно-малая. 
.
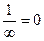Ответ. 0.
Задача 185(А,Б). Найти пределы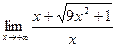 
, 
.
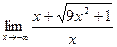Решение. Сейчас на этом примере мы увидим, как может отличаться ответ в зависимости от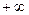 
или 
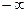. И в том, и в другом случае мы стараемся сократить дробь на множитель .
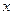Если 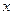положительно, то 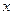можно представить в виде .
= 
= 
= 
= 
.
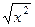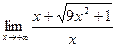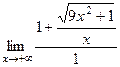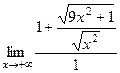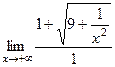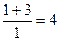А вот если 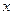отрицательно, то надо учесть, ч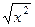то это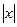 
, оно положительно, то есть при 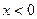верно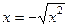 
. Поэтому
= 
= 
= 
.
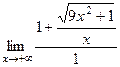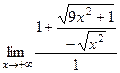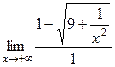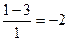Ответы. 4 и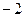 
.
Примеры, в которых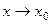 
.
|
|
Задача 186. Найти предел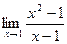 
.
Решение. В этом случае 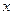стремится к числу, а не бесконечности. Получается неопределённость совсем другого типа: если в прошлых примерах было 
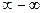или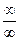 
, то здесь 
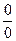. Если просто подставить 1 в это выражение, получилось бы 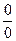. Поэтому и нельзя просто подставить и вычислить значение, а нужно раскрывать неопределённость. Выделим множитель 
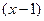и в числителе, и в знаменателе, чтобы его сократить.
= 
= 
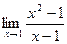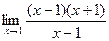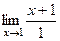= 2.
Когда сократили, тогда уже можно просто подставить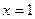 
.
Ответ. 2.
Задача 187. Найти предел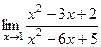 
.
Решение. Найдём корни многочленов в числителе и знаменателе, и разложим на множители.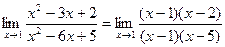 
=
= 
= 
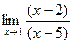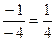. Сократили тот множитель, который отвечает за стремление к нулю, в числителе и знаменателе.
Ответ.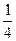 
.
Задача 188. Найти предел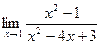 
.
Решение. Разложим на множители, как и в прошлой задаче.
= 
= 
= 
.
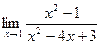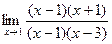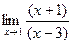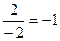Нашли корни числителя и знаменателя, разложили на множители. Сократили тот множитель, который отвечает за стремление к нулю, в числителе и знаменателе.
Ответ.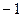 
.
Задача 189. Найти предел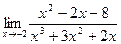 
.
Решение. Во-первых, если просто подставить 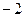, видно неопределённость 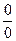. Это означает, что 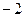является корнем, т.е. по крайней мере, хотя бы один множитель вида 
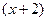и в числителе, и в знаменателе найдётся. Это облегчает поиск корней, можно обойтись даже без дискриминанта, а просто найти второй дополняющий. Когда мы сократим все 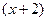, можно будет просто подставить 
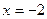в оставшееся выражение.
= 
= 
= 
= 
= 
.
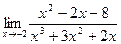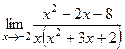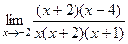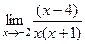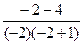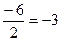Ответ.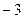 
.
Задача 190. Найти предел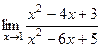 
.
Решение. Способ 1. Тот факт, что при подстановке 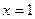и в числителе, и в знаменателе даёт значение 0, говорит о том, что множитель 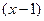присутствует хотя бы один раз. Поэтому найти корни можно даже без дискриминанта.
|
|
= 
= 
= 
= 
= 
.
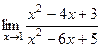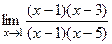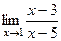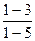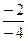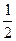Способ 2. (Лопиталя).
= 
= 
= 
= 
= .
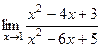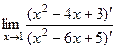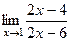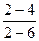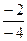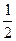Ответ. .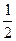
Задача 191. Найти предел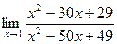 
.
Решение. Способ 1.
= 
= 
= 
= 
.
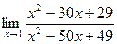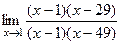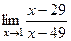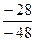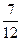Способ 2. =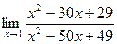 
= 
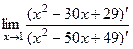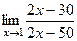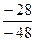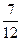= = . Ответ. .
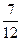Задача 192. Найти предел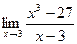 
.
Решение. Воспользуемся формулой разности кубов:
.
= 
= 
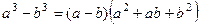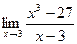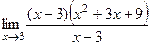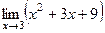= 27.
Впрочем, можно сделать и методом Лопиталя:
= 
= 
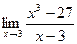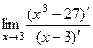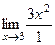= 27.
Ответ. 27.
Задача 193. Найти предел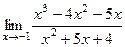 
.
Решение. =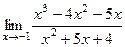 
= 
= 
= 
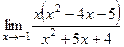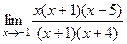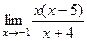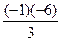= 2.
Ответ. 2.
Задача 194 (А,Б). Найт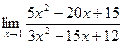и 
и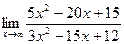 
.
Решение. Сразу вынесем за скобку общий множитель и в числителе, и в знаменателе, там все остальные коэффициенты ему кратны. Затем разложим на множители.
= 
= 
=
= 
= 
.
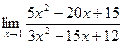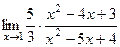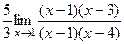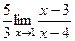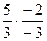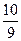А при 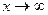другой тип неопределённости, и применяется совершенно другой метод решения, несмотря на то, что функция та же самая.
= 
= 
= 
.
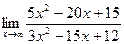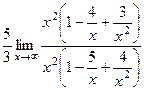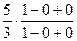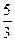Ответы. 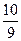и .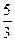
Замечание. Оба этих предела можно было найти по правилу Лопиталя.
= 
= 
= .
= 
= 
= .
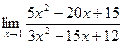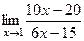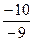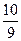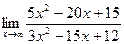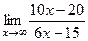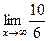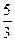Задача 195. Найти предел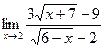 
.
Решение. Домножим и разделим на сопряжённое к каждой разности.
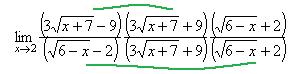
При этом соединим дугой те, которые в итоге сворачиваются в разность квадратов. Прочие множители, которые ни с чем не объединяются, вынесем в отдельную дробь, и даже в отдельный предел. Получается произведение пределов:
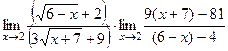
В одном из них нет неопределённости, а во втором преобразуем так, чтобы сократить скобку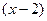 
.
= 
= 
= 
= .
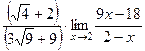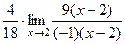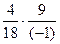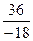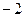Ответ. .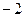
Задача 196. Найти предел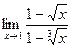 
.
Решение. В этом случае можно с помощью замены преобразовать так, что будут только целые степени, а для получившихся многочленов уже можно искать корни и проводить разложение на множители.
НОК(2,3) = 6. Если обозначим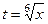 
, то:
, 
.
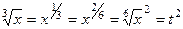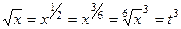При этом, если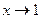 
, то и 
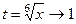тоже стремится к 1.
* Такое совпадение при замене переменной бывает далеко не всегда, а лишь в частных случаях, а обычно надо пересчитать, возможно новая переменная стремится к другому числу. Например, если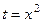 
и 
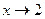, то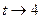 
.
|
|
Итак,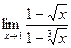 
= 
= 
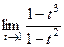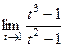(для удобства сделали, чтобы многочлены начинались со старшей степени). Далее,
= 
= 
= 
.
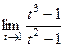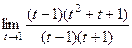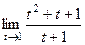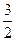При этом даже нет необходимости делать обратную замену и возвращаться к старой переменной.
Ответ. 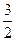.